37. Ряд Тейлора. Достаточное условие разложимости функции в ряд Тейлора

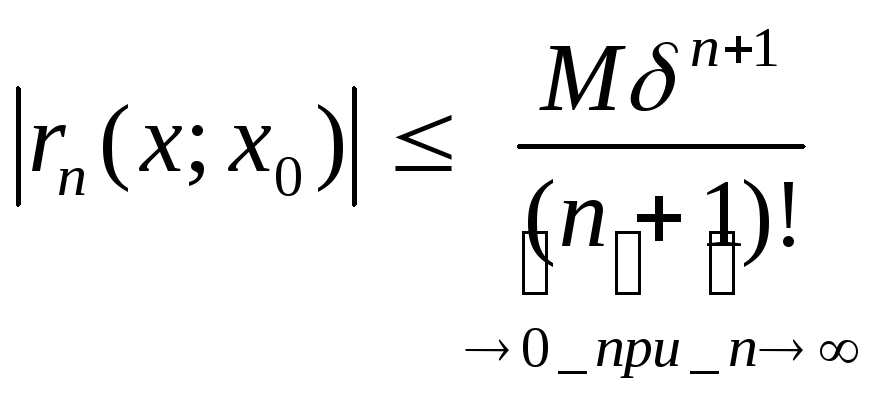
опр.:Пусть. Тогда рядназ-ся рядом Тейлора ф-иив точке. Если, топо ф-ле Тейлора:, где- остаточный член ф-лы Тейлора, т.е., где-n-ая частичная сумма ряда Тейлора ф-иив точке.ряд Тейлора сходится натогда и только тогда, когда.теор.:Пустьи, тогда надок-во: , где- остаточный член формулы Тейлора в форме Лагранжа. Рассм. ряд,по признаку Даламбера ряд сх-ся. Перейдем к пределеу прив неравенствена.

38. Разложение функций e^x, shx, chx в ряд Тейлора

1). Рассмотримввиду интервалаверно. Еслиx₀=0, тонаR.

2)наR. Еслиx₀=0, то.

3)наR.

39. Разложение функций sinx, cosx в ряд Тейлора

1)

наR.

2)

наR.

40. Разложение функций (1+x)^α, ln(1+x), arctgx в ряд Тейлора

1)

2)

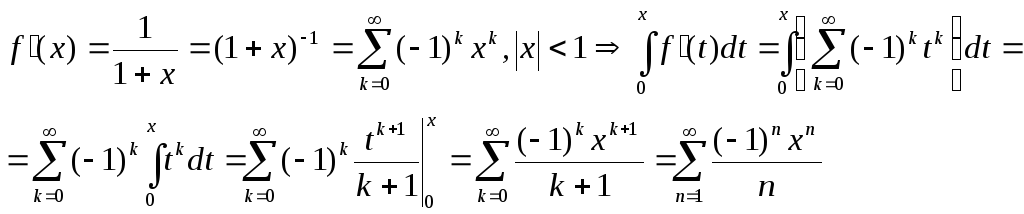
т.е.

3) ;

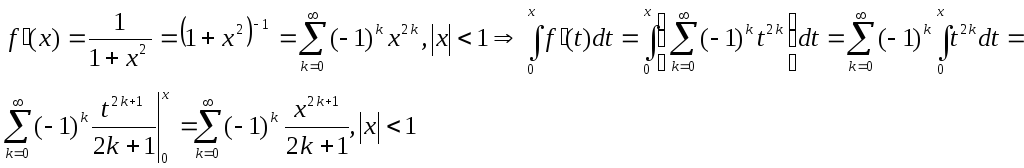т.е.

41. Тригонометрический ряд Фурье. Условие разложимости функции в ряд Фурье

Пусть , тогдасуществуют, приn=0.- это коэфф-ты ряда Фурье ф-ии .- ряд Фурье ф-ии на.опр.:Ф-я называется кусочно гладкой на [a;b], если сама ф-я и ее производные имеют на [a,b] конечное число точек разрыва 1-го рода.теор.:Пусть- периодическая ф-я, кусочно гладкая на. Тогда ее ряд Фурьесходится к значению в каждой ее точке непрерывности и к значениюв точках разрыва 1-го рода, где,

42. Преобразования Фурье. Интеграл Фурье

Пусть абсолютно интегрируема на, т.е.сх-ся. Тогдасуществует интеграл, т.к.сх-ся. Функцияназ-ся преобразованием Фурье функции . Ф-я определена наRи ограничена. Если абсолютно интегрируема на, то- обратное преобразование Фурье, или интеграл Фурье.замечание: