1. Двойной интеграл и его приложения

опр.ПустьD– обл. на плоскостиf:D→R. РазобьемDна более мелкие областиD₁,D₂, …D_n, не имеющие общих внутренних точек.В каждойD_k(k=1, …,n) выбираем произвольную точкуP_k(x_k,y_k) (k=1, …,n) и составляем сумму, где- площадь областиD_k. Это интегральная сумма функцииf, соответствующая разбиениюDна более мелкие области и выбору точекP_k(k=1, …,n).diamD_k=supS(M’,M’’),M’,M’’D_k.d= diamD_k– диаметр разбиенияDнаD₁,D₂, …D_n. Если существует, не зависящий от способа разбиенияDна более мелкие областиD₁,D₂, …D_nи от выбора точекP_kв них, тоэто значение редела есть двойной интеграл от ф-ииfпо областиD:теор. пустьD– замкнутая обл. на плоскости, функцияfнепрерывна вD. Тогдасуществует. Свойства двойного интеграла: 1.2.3. ЕслиD=D₁ U D₂, гдеD₁иD₂не имеют общих внутренних точек, тоПриложения двойного интеграла:1.=S(D) – площадь областиD2. Еслиf(x,y)0, то=V(G) – объем цилиндрического тела,G={(x,y,z)R³| 0zf(x,y), (x,y)D} 3. ЕсливD, то- масса пластинкиDплотностью4. Статические моменты пластинки относительно осейO_xиO_y:M_x=,M_y=5. Координаты центра масс пластинкиx_c=M_y/M,y_c=M_x/M6. Момент инерции пластинкиDотн-но осей координат и начала координат,,

2. Сведение двойного интеграла к повторному

о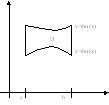пр.ОбластьD={}, гдеи- непрерывные функции на [a,b], называется стандартной отн-но осиO_y

опр.ОбластьD={}, гдеи- непрерывные функции на [c,d], называется стандартной отн-но осиO_x.

Если Dстандартна отн-но осиO_xиO_y, тоD- стандартная область.

т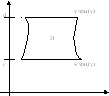еор.ЕслиD={} стандартна отн-но осиO_y, то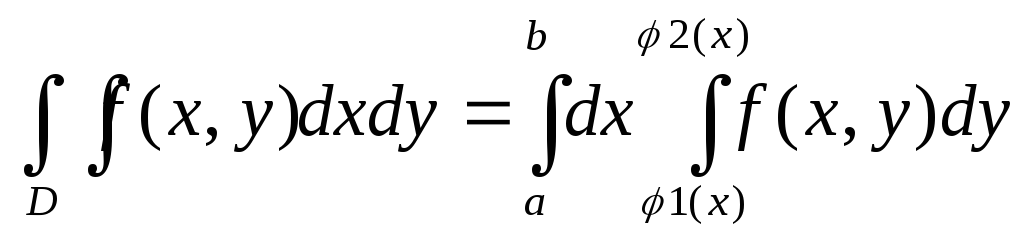-повторный интеграл

Если D={} - стандартна отн-но осиO_x, то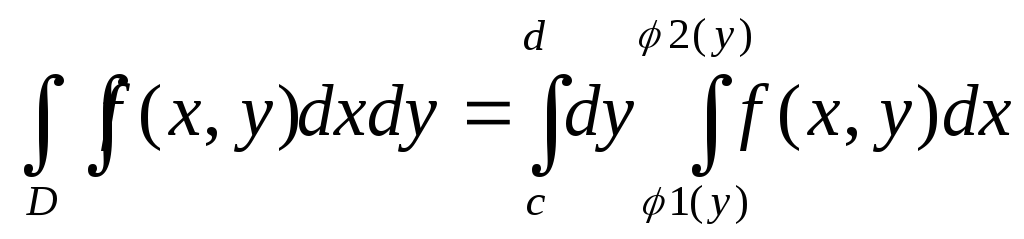. ЕслиD– стандартная область, то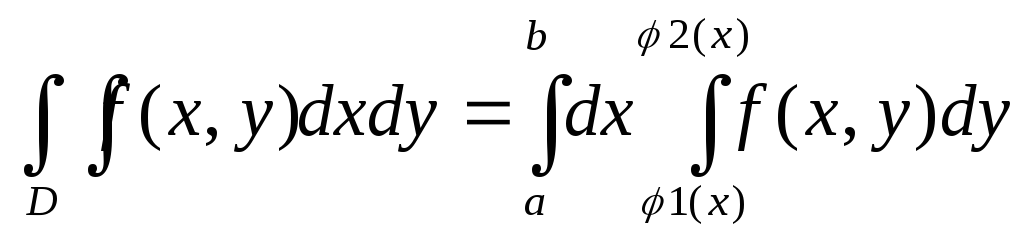=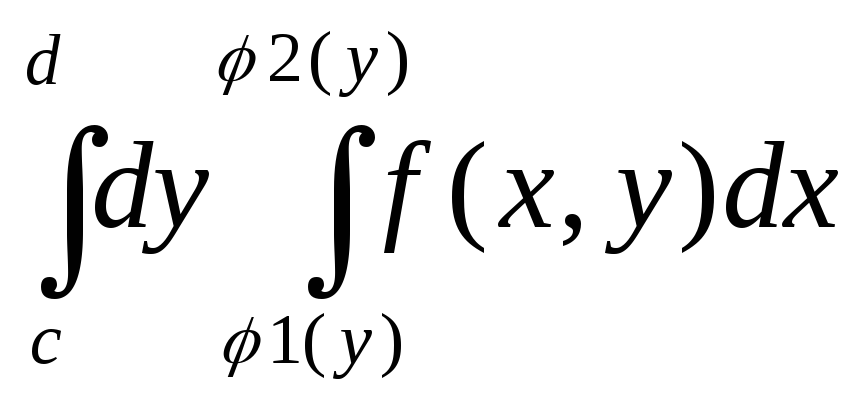- изменение порядка интегрирования.

3. Замена переменных в двойном интеграле. Переход к полярным и обобщенным полярным координатам

Перейдем к новым координатам (u,v), связь между старыми и новыми координатамиx=x(u,v),y=y(u,v). Если отображение, задаваемое этими формулами явл. непрерывно дифференцируемым взаимнооднозначным отображением и якобиан этого отображения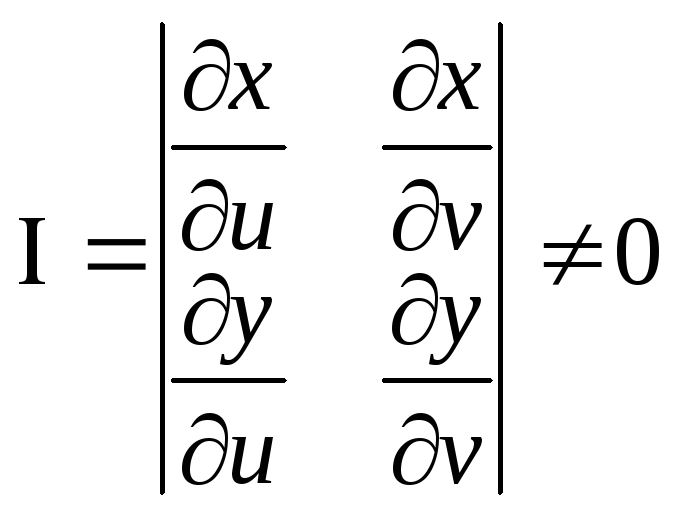в областиD*, то

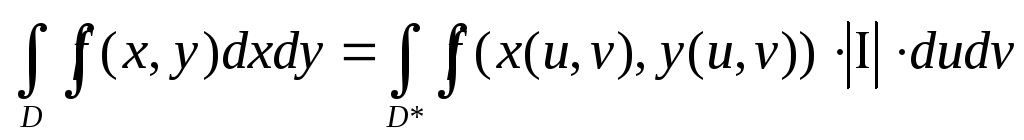
Переход к полярным корд-там:

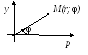
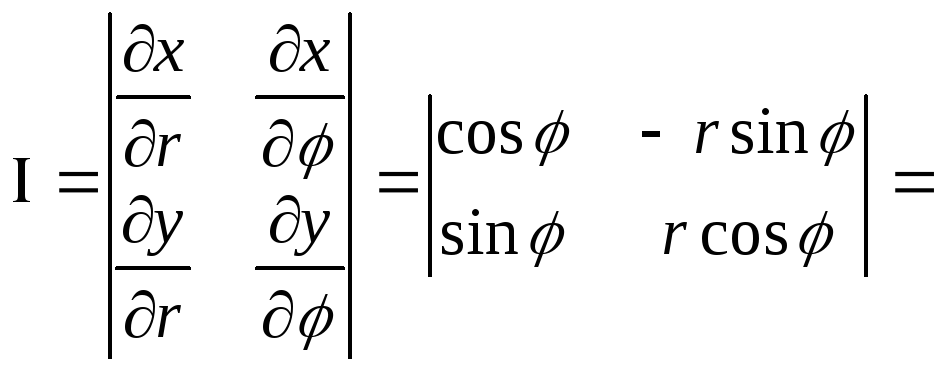
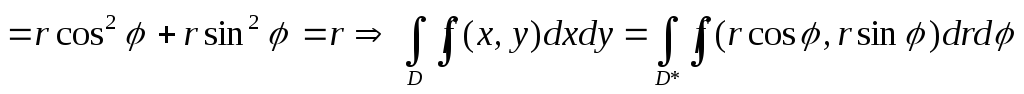
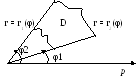
Переход к обобщенным полярным корд-там:

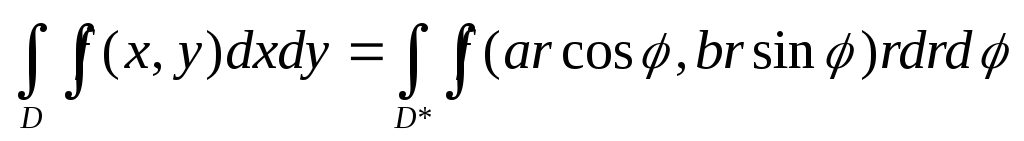
4. Тройной интеграл и его приложения. Вычисление тройного интеграла

- ограниченная замкнутая область в трехмерном пространстве.опр.:РазобьемGна более мелкие областиG₁, …,G_n, не имеющие общих внутренних точек:- диам. разбиенияGнаG₁, …,G_n. В каждой областиG_kвыбираем произвольную точкуP_k(x_k,y_k,z_k) и составляем интегральную сумму, где- объем областиG_k(k=1, …,n). Еслисуществует и не зависит от разбиенияGна более мелкие подобласти и от выбора точекP_k(k=1, …,n) в них, тоfинтегрируема по областиGи- тройной интеграл от ф-ииfпо областиG.теор.:ЕслиG– ограниченная замкнутая область вR³и ф-яfнепрерывна вG, то сущ-етСвойства тр. интеграла:1.2.для3. ЕслиG=G₁UG₂, гдеG₁иG₂не имеют общих внутренних точек, тоПриложения тр. ин-ла:1.=V(G) – объем областиG2. Если-плотность в-ва, находящегося в обл.G, то масса телаG-3. Статические моменты телаGот-но корд. плоскостейxOy,xOz,yOz:,,4. Корд-ты центра масс телаG:x_c=M_yz/m,y_c=M_xz/m,z_c=M_xy/m, гдеm- масса телаG5. Моменты инерции тела отн-но корд плоскостей и начала корд-т:,,,I_x=I_xy+I_xz,I_y=I_xy+I_yz,I_z=I_xz+I_yz ,I₀=I_xy+I_xz+I_yzВычисление тр. инт-ла:ЕслиGявл. 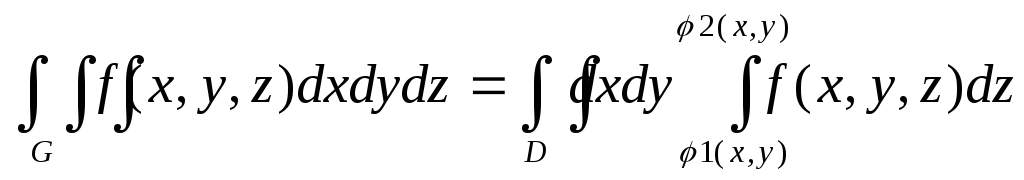стандартной обл-тью отн-но осиO_z, т.е., тоАналогично вычисляется дляG, стандартной отн-ноO_xиO_y