
- •1. Двойной интеграл и его приложения
- •2. Сведение двойного интеграла к повторному
- •3. Замена переменных в двойном интеграле. Переход к полярным и обобщенным полярным координатам
- •4. Тройной интеграл и его приложения. Вычисление тройного интеграла
- •5. Замена переменных в тройном интеграле. Переход к цилиндрическим, сферическим и обобщенным сферическим координатам
- •6. Криволинейный интеграл первого рода и его основные свойства. Вычисление криволинейных интегралов первого рода
- •7. Ориентация кривой
- •8. Криволинейный интегралы второго рода, их осн. Свойства. Вычисление криволинейных интегралов второго рода.
- •9. Формула Грина
- •10. Поверхностный интегралы первого рода и их осн. Свойства. Вычисление поверхностных интегралов 1-го рода.
- •11. Дифференциальные уравнения первого порядка. Основные понятия
- •12. Дифференциальное уравнение первого порядка с разделяющимися переменными
- •19. Дифференциальные уравнения высших порядков. Основные понятия
- •20. Дифференциальные уравнения высших порядков, допускающие понижение порядка
- •21. Линейные дифференциальные уравнения высших порядков
- •22. Линейные дифференциальные уравнения высших порядков с постоянными коэффициентами
- •23. Нормальные системы дифференциальных уравнений и их решение методом исключения неизвестных
- •24. Определение числового ряда и его сходимость. Необходимое условие сходимости числового ряда
- •25. Свойства сходящихся числовых рядов
- •26. Сходимость числовых рядов с неотрицательными членами
- •27. Признаки сравнения для числовых рядов с неотрицательными членами.
- •28. Признак Даламбера для числовых рядов с неотрицательными членами
- •33. Функциональный ряд и его сходимость. Признаки Даламбера и Коши для исследования сходимости функциональных рядов
- •34. Признак равномерной сходимости Вейерштрасса
- •35. Степенной ряд. Радиус сходимости и интервал сходимости степенного ряда
- •36. Свойства степенных рядов. Единственность разложения функции в степенной ряд
- •37. Ряд Тейлора. Достаточное условие разложимости функции в ряд Тейлора
- •42. Преобразования Фурье. Интеграл Фурье
23. Нормальные системы дифференциальных уравнений и их решение методом исключения неизвестных
Система дифф. ур-ий вида
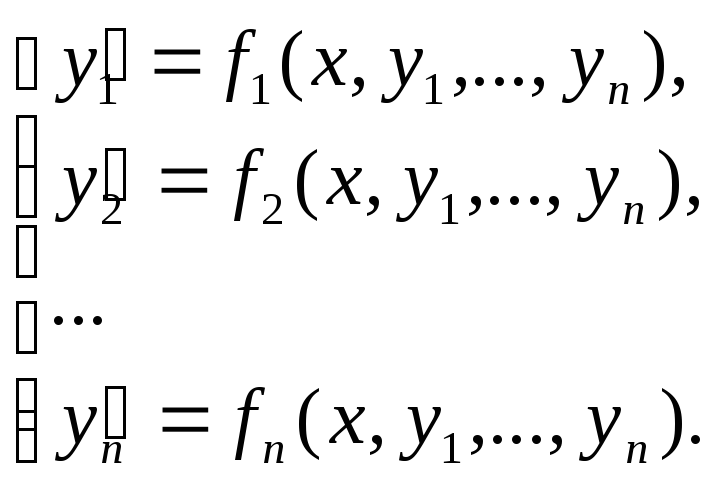 ,
гдеx– независимая
переменная,
,
гдеx– независимая
переменная,![]() - неизвестные функции, наз-ся нормальной
системой дифф. ур-ий. решением этой
системы назыв. набор изnф-ий
- неизвестные функции, наз-ся нормальной
системой дифф. ур-ий. решением этой
системы назыв. набор изnф-ий![]() ,
при подстановке которых в каждое ур-е
системы получается тождество. Решение
задачи Коши для этой системы: нахождение
решений этой системы, удовл. заданным
начальным условиям
,
при подстановке которых в каждое ур-е
системы получается тождество. Решение
задачи Коши для этой системы: нахождение
решений этой системы, удовл. заданным
начальным условиям![]() .
Каждую нормальную систему можно свести
к дифф. ур-ю с одной неизвестной ф-ей.
Это происходит путем исключения
неизвестных.
.
Каждую нормальную систему можно свести
к дифф. ур-ю с одной неизвестной ф-ей.
Это происходит путем исключения
неизвестных.
24. Определение числового ряда и его сходимость. Необходимое условие сходимости числового ряда
опр.:Бесконечная сумма![]() ,
где
,
где![]() наз-ся
числовым рядом.
наз-ся
числовым рядом.![]() n-ая
частичная сумма
n-ая
частичная сумма![]() получается
последовательность частичных суммSnряда. ЕслиSnсходится, то ряд сходится и его сумма
равна
получается
последовательность частичных суммSnряда. ЕслиSnсходится, то ряд сходится и его сумма
равна![]() .
Если жеSnрасходится, то ряд также расходится.теор.:Если ряд
.
Если жеSnрасходится, то ряд также расходится.теор.:Если ряд![]() сходится,
то
сходится,
то![]() .следствие:Если
.следствие:Если![]() или
не сущ-ет, то
или
не сущ-ет, то![]() расходится.док-во:Пусть
расходится.док-во:Пусть![]() сходится,
тогда
сходится,
тогда![]() .
.![]()
25. Свойства сходящихся числовых рядов
теор.:Пусть ряды![]() и
и![]() сх-ся,
причем
сх-ся,
причем![]() и
и![]() ,
тогда:1)
,
тогда:1)![]()
![]() сх-ся и
сх-ся и![]() ;2)
;2)![]() сх-ся и
сх-ся и![]() ;3)
;3)![]() -n-ый остаток ряда
-n-ый остаток ряда![]() ,
,![]() док-во:1)Рассм.
док-во:1)Рассм.![]() .
.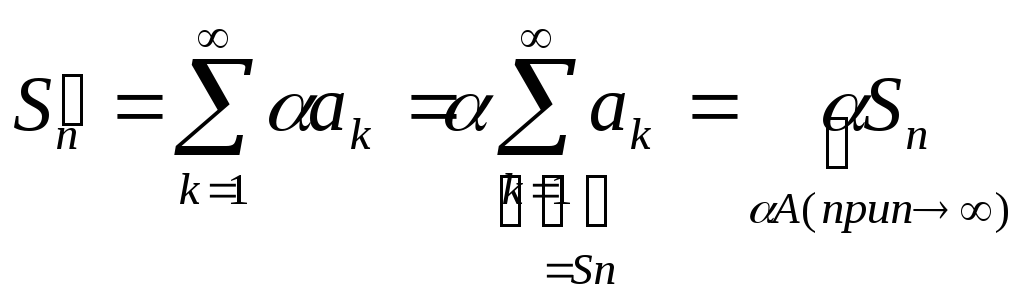
![]() ;2)Рассм.
;2)Рассм.![]() .
.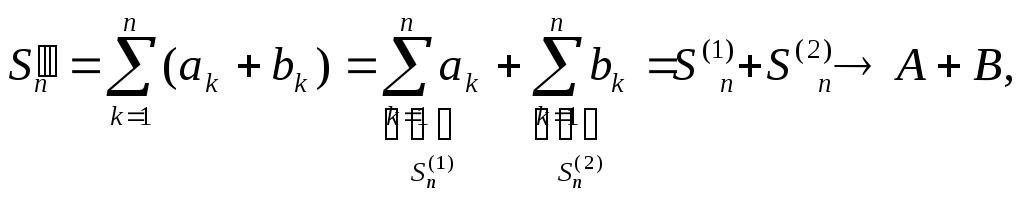
![]() ;3)
;3)![]() .
.
26. Сходимость числовых рядов с неотрицательными членами
![]() ,
где
,
где![]() -
числовой ряд с неотрицат. членами.
-
числовой ряд с неотрицат. членами.![]() посл-ть
частичных сумм
посл-ть
частичных сумм![]() - неубывающая посл-ть, отсюда
- неубывающая посл-ть, отсюда![]() сходится тогда и только тогда, когда
сходится тогда и только тогда, когда![]() ограничена сверху
ограничена сверху![]() вернатеорема:Ряд с неотрицат. членами
сх-ся тогда и только тогда, когда
вернатеорема:Ряд с неотрицат. членами
сх-ся тогда и только тогда, когда![]() ограничена сверху.
ограничена сверху.
27. Признаки сравнения для числовых рядов с неотрицательными членами.
теор.:Пусть![]() и
и![]() -
числовые ряды с неотрицат. членами,
-
числовые ряды с неотрицат. членами,![]() ,
тогда:1)Если
,
тогда:1)Если![]() сх-ся,
тогда
сх-ся,
тогда![]() тоже сходится;2)Если
тоже сходится;2)Если![]() расходится, то
расходится, то![]() тоже расх-ся.следствие:Если
тоже расх-ся.следствие:Если![]() ,
то ряды сх-ся или расх-ся одновременно.док-во:
,
то ряды сх-ся или расх-ся одновременно.док-во:
![]() если
если![]()
![]() ,
,![]() если
если![]() сх-ся,
то
сх-ся,
то![]() ограничена
сверху
ограничена
сверху![]() ограничена
сверху
ограничена
сверху![]() сх-ся.
Если же
сх-ся.
Если же![]() расходится, то
расходится, то![]() неограничена сверху
неограничена сверху![]() неогран. сверху
неогран. сверху![]() расх-ся.
расх-ся.![]() ,
т.е.
,
т.е.![]() для
для![]()
![]()
![]()
![]() ,
т.е.
,
т.е.![]()
![]()
![]()
![]() .
Из теоремы следует, что ряды сходятся
или расходятся одновременно.
.
Из теоремы следует, что ряды сходятся
или расходятся одновременно.
28. Признак Даламбера для числовых рядов с неотрицательными членами
теор.:![]() - числовой ряд с положит. членами и
- числовой ряд с положит. членами и![]() .
Тогда:1)q<1 – ряд
сх-ся;2)q>1 – ряд
сх-ся;3)q=0 – требуется
дополнит. исследование.док-во:1)q<1. Возьмем
.
Тогда:1)q<1 – ряд
сх-ся;2)q>1 – ряд
сх-ся;3)q=0 – требуется
дополнит. исследование.док-во:1)q<1. Возьмем![]() ,
тогда
,
тогда![]() ,
т.е.
,
т.е.![]() и
т.д. Получаем, что
и
т.д. Получаем, что![]()
![]() .
Рассм. ряд
.
Рассм. ряд![]() - сх-ся, отсюда по признаку сравнения
- сх-ся, отсюда по признаку сравнения![]() сх-ся;2)q>1. Возьмем
сх-ся;2)q>1. Возьмем![]() ,
тогда
,
тогда![]() ,
т.е.
,
т.е.![]() и
т.д. Получаем, что
и
т.д. Получаем, что![]()
![]() .
.![]()
![]() расх-ся.3)q=1. Рассм.
ряд
расх-ся.3)q=1. Рассм.
ряд![]() - он сх-ся.
- он сх-ся.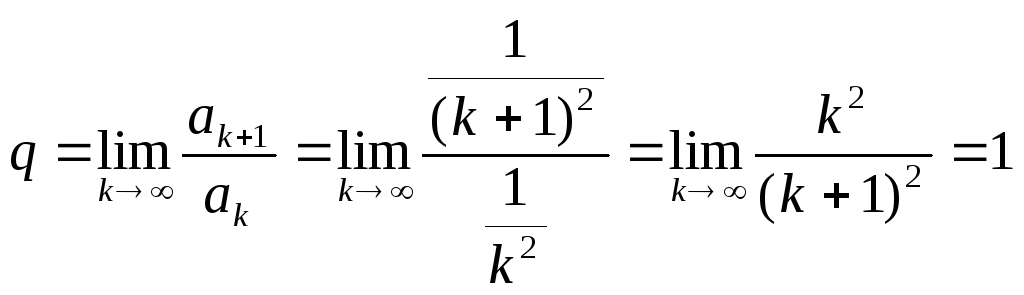 .
Рассм.
.
Рассм.![]() - расходится,
- расходится,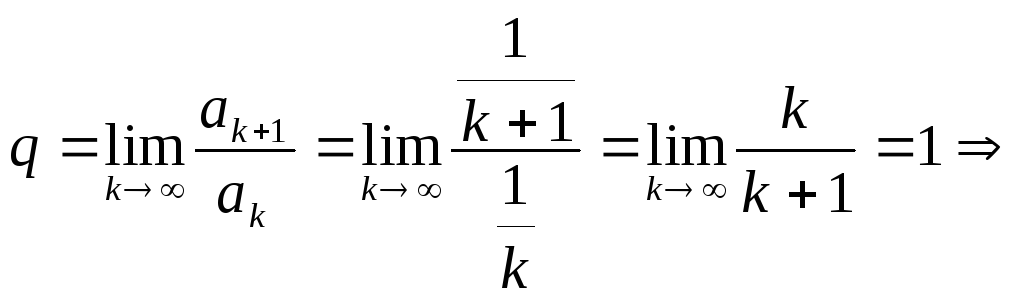 нужно
дополнительное исследование.
нужно
дополнительное исследование.
29. Радикальный признак Коши для числовых рядов с неотрицательными членами
теор.:![]() -
числовой ряд с неотриц. членами и
-
числовой ряд с неотриц. членами и![]() .
Тогда:1)q<1 – ряд
сх-ся;2)q>1 – ряд
сх-ся;3)q=0 – требуется
дополнит. исследование.док-во:1)q<1. Возьмем
.
Тогда:1)q<1 – ряд
сх-ся;2)q>1 – ряд
сх-ся;3)q=0 – требуется
дополнит. исследование.док-во:1)q<1. Возьмем![]() ,
тогда
,
тогда![]() .
Рассм.
.
Рассм.![]() -
сх-ся, т.к.
-
сх-ся, т.к.![]() по
признаку сравнения
по
признаку сравнения![]() сх-ся;2)q<1. Возьмем
сх-ся;2)q<1. Возьмем![]() ,
тогда
,
тогда![]()
![]() расх-ся;3)q=1. Рассм.
ряд
расх-ся;3)q=1. Рассм.
ряд![]() - он сх-ся.
- он сх-ся.![]() .
Рассм.
.
Рассм.![]() - расходится,
- расходится,![]() нужно
дополнительное исследование.
нужно
дополнительное исследование.
30. Интегральный признак Коши для числовых рядов с неотрицательными членам
теор.:![]() -
числовой ряд с неотриц. членами,
-
числовой ряд с неотриц. членами,![]() - невозрастающая ф-я.
- невозрастающая ф-я.![]()
![]() .
Тогда
.
Тогда![]() сх-ся
или расх-ся одновременно с
сх-ся
или расх-ся одновременно с![]() док-во:Возьмем
док-во:Возьмем![]() и
рассмотрим [k,k+1].
и
рассмотрим [k,k+1].![]()
![]() .
Проинтегрируем это неравенство по [k,k+1]:
.
Проинтегрируем это неравенство по [k,k+1]: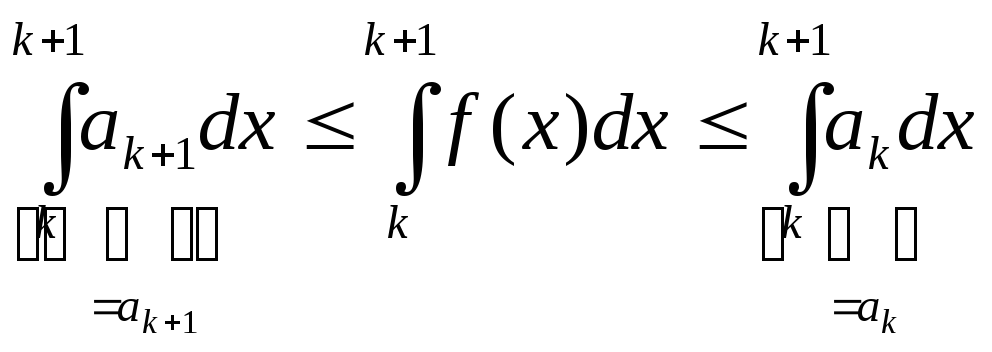 ,
т.е.
,
т.е.![]()
![]()
![]()
![]() ;
;![]()
![]() .
Если
.
Если![]() сх-ся, то
сх-ся, то![]()
![]() .
Рассм.
.
Рассм.![]() .
.![]()
![]()
![]() ,
где
,
где![]() - неубывающая ф-я, огран. сверху числомS
- неубывающая ф-я, огран. сверху числомS![]() - конечный. Пусть
- конечный. Пусть![]() расх-ся, тогда
расх-ся, тогда![]() расх-ся. Пусть
расх-ся. Пусть![]() сх-ся иn=I
сх-ся иn=I![]() и
и![]()
![]() .
.![]() - неубывающая последовательность,
ограниченная сверху
- неубывающая последовательность,
ограниченная сверху![]() - конечный, и, значит, ряд сх-ся.
- конечный, и, значит, ряд сх-ся.
![]()
![]() .
Пусть
.
Пусть![]() расх-ся
расх-ся![]()
![]() ряд
расх-ся.
ряд
расх-ся.
31. Знакочередующиеся числовые ряды. Признак Лейбница
опр.:Ряд вида![]() ,
где
,
где![]()
![]() ,
наз-ся знакочередующимся.
,
наз-ся знакочередующимся.![]() теор.:Пусть
теор.:Пусть![]() - знакочередующийся ряд. Если 1)
- знакочередующийся ряд. Если 1)![]()
![]() ,
2)
,
2)![]() ,
то этот ряд сходится.док-во:
,
то этот ряд сходится.док-во:![]() ;
;![]() ;
;![]()
![]() ,
но
,
но![]() ,
т.е.
,
т.е.![]() - невозрастающая посл-ть.
- невозрастающая посл-ть.![]() ,
т.е.
,
т.е.![]() еще и ограничена снизу. Следовательно
еще и ограничена снизу. Следовательно![]() .
.![]()
![]() ,
т.е.
,
т.е.![]() -
неубывающая посл-ть.
-
неубывающая посл-ть.![]()
![]()
![]() ограничена сверху, следовательно
ограничена сверху, следовательно![]() .
.![]() - перейдем к пределу при
- перейдем к пределу при![]() ,
получим, что
,
получим, что![]()
![]()
![]()
![]()
![]() и
и![]() если
взять
если
взять![]() ,
то
,
то![]()
![]() ,
т.е. ряд сходится.
,
т.е. ряд сходится.
32. Абсолютная и условная сходимость числовых рядов. Признаки Даламбера и Коши для произвольных числовых рядов
опр.:Ряд![]() абсолютно сходится, если сходится ряд
абсолютно сходится, если сходится ряд![]() .опр.:Если ряд
.опр.:Если ряд![]() сх-ся, но не абсолютно, то он сходится
условно.теор.(признак Даламбера для
произв. рядов):
сх-ся, но не абсолютно, то он сходится
условно.теор.(признак Даламбера для
произв. рядов):![]() - произв. числовой ряд. Пусть
- произв. числовой ряд. Пусть![]() ,
тогда если:1)q<1, то
ряд абс. сх-ся,2)q>1,
то ряд абс. расх-ся,3)q=1,
то нужно доп. исслед-е.док-во:1)q<1
,
тогда если:1)q<1, то
ряд абс. сх-ся,2)q>1,
то ряд абс. расх-ся,3)q=1,
то нужно доп. исслед-е.док-во:1)q<1![]() по пр. Даламбера для рядов с неотрицат.
членами
по пр. Даламбера для рядов с неотрицат.
членами![]() сх-ся, следовательно
сх-ся, следовательно![]() абсол. сх-ся;2)q>1.
Рассм.
абсол. сх-ся;2)q>1.
Рассм.![]() расх-ся.теор.(радикальный признак
Коши для рядов с произвольными членами):
расх-ся.теор.(радикальный признак
Коши для рядов с произвольными членами):![]() - ряд с произв. членами. Пусть
- ряд с произв. членами. Пусть![]() ,
тогда если:1)q<1, то
ряд абс. сх-ся,2)q>1,
то ряд абс. расх-ся,3)q=1,
то нужно доп. исслед-е.док-во:1)q<1. по признаку
Коши для рядов с неотрицат. членами
,
тогда если:1)q<1, то
ряд абс. сх-ся,2)q>1,
то ряд абс. расх-ся,3)q=1,
то нужно доп. исслед-е.док-во:1)q<1. по признаку
Коши для рядов с неотрицат. членами![]() сх-ся, следовательно
сх-ся, следовательно![]() абсол. сх-ся;2)q>1.
Рассм.
абсол. сх-ся;2)q>1.
Рассм.![]() расх-ся.теор.:Если ряд абсолютно
сх-ся, то он сходится.
расх-ся.теор.:Если ряд абсолютно
сх-ся, то он сходится.
