
- •1. Двойной интеграл и его приложения
- •2. Сведение двойного интеграла к повторному
- •3. Замена переменных в двойном интеграле. Переход к полярным и обобщенным полярным координатам
- •4. Тройной интеграл и его приложения. Вычисление тройного интеграла
- •5. Замена переменных в тройном интеграле. Переход к цилиндрическим, сферическим и обобщенным сферическим координатам
- •6. Криволинейный интеграл первого рода и его основные свойства. Вычисление криволинейных интегралов первого рода
- •7. Ориентация кривой
- •8. Криволинейный интегралы второго рода, их осн. Свойства. Вычисление криволинейных интегралов второго рода.
- •9. Формула Грина
- •10. Поверхностный интегралы первого рода и их осн. Свойства. Вычисление поверхностных интегралов 1-го рода.
- •11. Дифференциальные уравнения первого порядка. Основные понятия
- •12. Дифференциальное уравнение первого порядка с разделяющимися переменными
- •19. Дифференциальные уравнения высших порядков. Основные понятия
- •20. Дифференциальные уравнения высших порядков, допускающие понижение порядка
- •21. Линейные дифференциальные уравнения высших порядков
- •22. Линейные дифференциальные уравнения высших порядков с постоянными коэффициентами
- •23. Нормальные системы дифференциальных уравнений и их решение методом исключения неизвестных
- •24. Определение числового ряда и его сходимость. Необходимое условие сходимости числового ряда
- •25. Свойства сходящихся числовых рядов
- •26. Сходимость числовых рядов с неотрицательными членами
- •27. Признаки сравнения для числовых рядов с неотрицательными членами.
- •28. Признак Даламбера для числовых рядов с неотрицательными членами
- •33. Функциональный ряд и его сходимость. Признаки Даламбера и Коши для исследования сходимости функциональных рядов
- •34. Признак равномерной сходимости Вейерштрасса
- •35. Степенной ряд. Радиус сходимости и интервал сходимости степенного ряда
- •36. Свойства степенных рядов. Единственность разложения функции в степенной ряд
- •37. Ряд Тейлора. Достаточное условие разложимости функции в ряд Тейлора
- •42. Преобразования Фурье. Интеграл Фурье
9. Формула Грина
т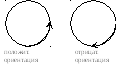 еор.:ПустьL– непрерывно
дифференцируемая замкнутая положительно
ориентированная кривая на плоскости,
функцииP(x,y)
иQ(x,y)
непрерывно дифференцируемы в обл.D,
границей которой явл.L,
тогда
еор.:ПустьL– непрерывно
дифференцируемая замкнутая положительно
ориентированная кривая на плоскости,
функцииP(x,y)
иQ(x,y)
непрерывно дифференцируемы в обл.D,
границей которой явл.L,
тогда![]()
![]()
10. Поверхностный интегралы первого рода и их осн. Свойства. Вычисление поверхностных интегралов 1-го рода.
Пусть
![]() -
поверхность в трехмерном пространстве.
Функция
-
поверхность в трехмерном пространстве.
Функция![]() .
разобьем произвольноSна более мелкие частиS1,S2, …,Sn,
.
разобьем произвольноSна более мелкие частиS1,S2, …,Sn,
![]() ,
причемSiиSj
,
причемSiиSj![]() не имеют общих внутренних точек. В каждойSkвыберем произвольную точку
не имеют общих внутренних точек. В каждойSkвыберем произвольную точку![]() и
составим интегральную сумму
и
составим интегральную сумму![]() .
Пусть
.
Пусть![]() =max
=max![]() .
Если
.
Если![]() и
и![]() существует и зависит от способа деленияSна более мелкие частиS1,S2,
…,Snи выбора точекMkв них, то он называется поверхностным
интегралом 1-го роа от функцииfповерхностиSи обозначается
существует и зависит от способа деленияSна более мелкие частиS1,S2,
…,Snи выбора точекMkв них, то он называется поверхностным
интегралом 1-го роа от функцииfповерхностиSи обозначается![]() теор.:Еслиfнепрерывна наSто
теор.:Еслиfнепрерывна наSто![]() существует.Свойства:1.
существует.Свойства:1.![]() 2.
2.![]() 3.
ЕслиS=S1US2,
гдеS1иS2не имеют общих внутр. точк, то
3.
ЕслиS=S1US2,
гдеS1иS2не имеют общих внутр. точк, то![]() Вычисление:Если пов-тьSзадана уравнением
Вычисление:Если пов-тьSзадана уравнением![]() ,
то
,
то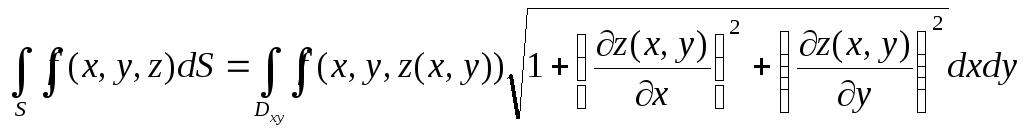 .
Еслиf=1 наS,
то
.
Еслиf=1 наS,
то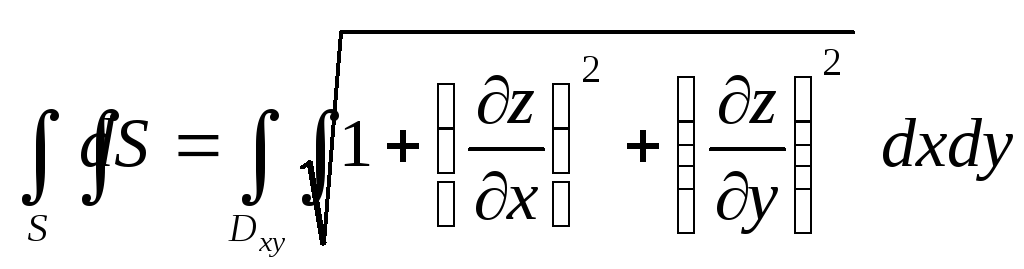 -
площадь поверхностиS
-
площадь поверхностиS
11. Дифференциальные уравнения первого порядка. Основные понятия
опр.:Дифференциальное Ур-е видаy’=f(x,y) илиF(x,y,y’)=0, гдеx– независимая переменная,y=y(x), аy’ – ее производная по переменнойx, называется дифференциальным уравнением первого порядка. опр.: Решением (частным решением) дифф. ур-я первого порядка на (a,b) называется ф-яy=φ(x), при подстановке которой вместе с ее производной в дифф. ур-е, получается тождество, выполняемое на всей (a,b). Ур-е Ф(x,y)=0, неявно задающее это решение, наз-ся интегралом (частным интегралом) дифф. ур-я первого порядка.опр.:Ф-яy= φ(x,C) наз-ся общим решением дифф. ур-я первого порядка, если 1) при каждом допустимом значении параметра С эта ф-я явл. частным решением этого дифф. ур-я; 2) каждое частное решение можно записать в видеy= φ(x,C0) при некотором значении параметра С=С0. Ур-е Ф(x,y,C)=0, неявно задающее общее решение дифф. ур-я первого порядка, наз-ся общим интегралом этого дифф. ур-я.
12. Дифференциальное уравнение первого порядка с разделяющимися переменными
Это ур-е вида y’=f1(x)f2(y).
Разделяем переменные:![]() Интегрируем левую часть равенства поy, правую поxи получаем общий интеграл дифф. ур-я:
Интегрируем левую часть равенства поy, правую поxи получаем общий интеграл дифф. ур-я:![]()
Замечание: если при y=y0f2(y0)=0, тоy=y0 явл. решением данного дифф. ур-я и в процессе решения оно может быть потеряно.
13. Однородные дифференциальные уравнения первого порядка
Это ур-я, кот. можно привести к виду
![]() .
Нужно сделать подстановку
.
Нужно сделать подстановку![]() ,
в рез-те получим ур-е с разделяющимися
переменными.
,
в рез-те получим ур-е с разделяющимися
переменными.
14. Линейные дифференциальные уравнения первого порядка
Это ур-я вида
![]() ,
где
,
где![]() и
и![]() -
ф-ии, зависящие только отx.
Решение линейных ур-ий первого порядка:
1) решаем ур-е
-
ф-ии, зависящие только отx.
Решение линейных ур-ий первого порядка:
1) решаем ур-е![]() - линейное однородное дифф. ур-е первого
порядка, при этом
- линейное однородное дифф. ур-е первого
порядка, при этом![]() .
Разделим переменные:
.
Разделим переменные:![]() -
общее решение 2) Метод вариации постоянной:
считаем, чтоC=C(x)
и находим решение ур-я
-
общее решение 2) Метод вариации постоянной:
считаем, чтоC=C(x)
и находим решение ур-я![]() в
виде
в
виде![]() ,
тогда
,
тогда![]() Подставимyиy’
в ур-е
Подставимyиy’
в ур-е![]() :
: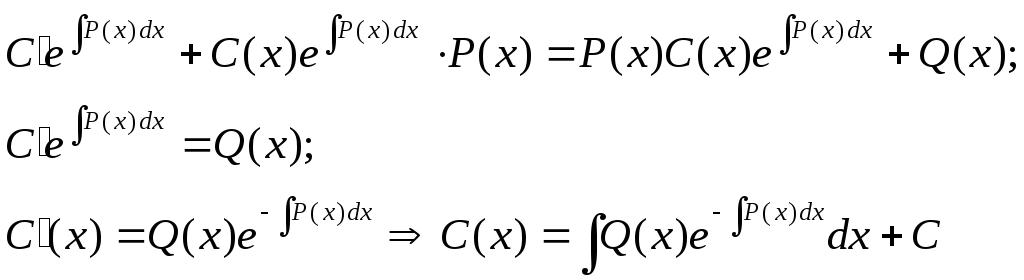
В итоге:
![]() -
общее решение ур-я
-
общее решение ур-я![]()
15. Уравнение Бернулли
Это дифф. ур-е первого порядка вида
![]() ,
где
,
где![]() Подстановка
Подстановка![]() сводит
это ур-е к линейному дифф. ур-ю первого
порядка:
сводит
это ур-е к линейному дифф. ур-ю первого
порядка:![]() Подставим это в исходное ур-е:
Подставим это в исходное ур-е:![]() ;
;![]() - линейное дифф. ур-е первого порядка
- линейное дифф. ур-е первого порядка
16. Дифференциальные уравнения первого порядка в полных дифференциалах
Это ур-я вида
![]() ,
где
,
где![]() ,
,![]() - некоторая ф-я,
- некоторая ф-я,![]() явл. уравнением в полных дифф-лах тогда
и только тогда, когда
явл. уравнением в полных дифф-лах тогда
и только тогда, когда![]() .
В этом случае ф-я
.
В этом случае ф-я![]() сущ-ет и ур-е можно записать так:
сущ-ет и ур-е можно записать так:![]() -
общий интеграл исходного ур-я и нужно
найти эту функцию
-
общий интеграл исходного ур-я и нужно
найти эту функцию![]() :
:![]() ,
где
,
где![]() -
некоторая ф-я, зависящая только отy.
-
некоторая ф-я, зависящая только отy.![]() -
это ур-е для нахождения ф-ии
-
это ур-е для нахождения ф-ии![]()
17. Дифференциальные уравнения первого порядка не разрешенные относительно производной
Пусть дифф. ур-е
![]() можно
записать в виде
можно
записать в виде![]() или
или![]() Введем параметр
Введем параметр![]() .
Тогда решение первого ур-я находится
из системы
.
Тогда решение первого ур-я находится
из системы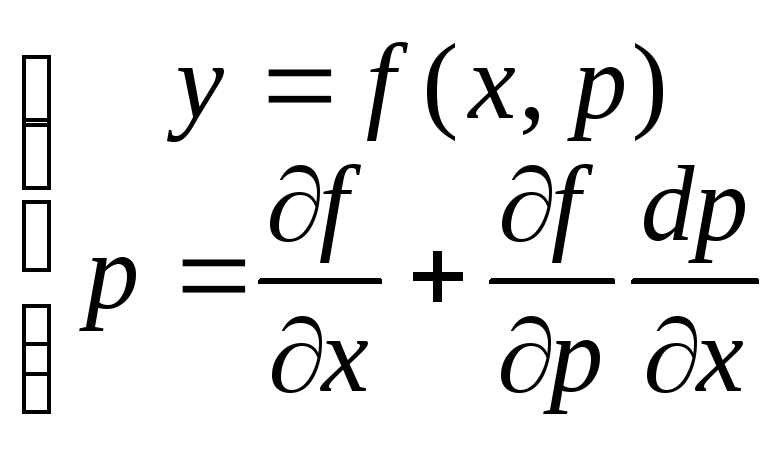 ,
а второго из
,
а второго из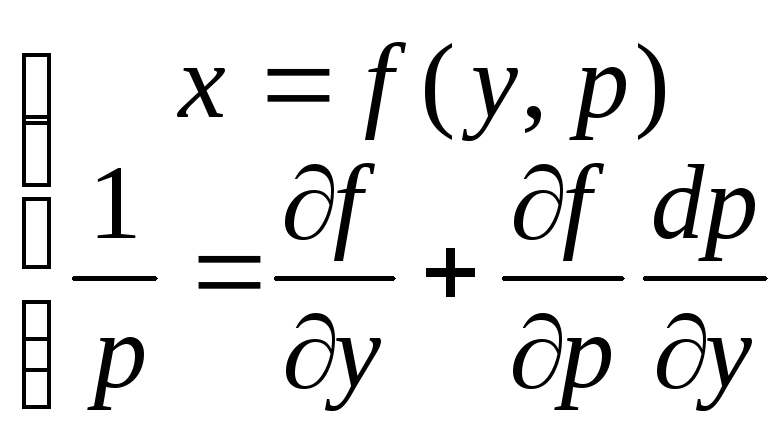 .
В общем случае решение получается
заданным параметрически.
.
В общем случае решение получается
заданным параметрически.
18. Теорема о существовании и единственности решения дифференциального уравнения первого порядка. Особые решения
опр.:Задача Коши для дифф. ур-я![]() -
это задача нахождения частного решения
этого ур-я, удовлетворяющего начальному
условию
-
это задача нахождения частного решения
этого ур-я, удовлетворяющего начальному
условию
![]() теорема о существовании и единственности
задачи Коши:Пусть у дифф. ур-я
теорема о существовании и единственности
задачи Коши:Пусть у дифф. ур-я![]() функция
функция![]() непрерывна в областиDплоскостиxOyи
непрерывна в областиDплоскостиxOyи![]() ограничена вD. Тогда
ограничена вD. Тогда![]()
сущ-ет и единственно на промежутке
![]() частное
решение этого ур-я
частное
решение этого ур-я![]() ,
удовл. начальному условию
,
удовл. начальному условию![]() .замечание:Кривая
.замечание:Кривая![]() ,
на которой ф-я
,
на которой ф-я![]() -
частное решение дифф. ур-я
-
частное решение дифф. ур-я![]() наз-ся
интегральной кривой. След-но в услових
теоремы через
наз-ся
интегральной кривой. След-но в услових
теоремы через![]() точку
точку![]() единственная
интегральная кривая этого ур-я.опр.:Точки областиD, в которых
нарушается единственность решения
задачи Коши, наз-ся особыми точками
дифф. ур-я.опр.:Решение дифф.
ур-я
единственная
интегральная кривая этого ур-я.опр.:Точки областиD, в которых
нарушается единственность решения
задачи Коши, наз-ся особыми точками
дифф. ур-я.опр.:Решение дифф.
ур-я![]() ,
в каждой точке которого нарушается
единственность решения задачи Коши,
наз-ся особым решением этого ур-я. особые
решения не получаются из общего решения
ни при каких значениях параметраC.нахождение особого значения:1) Если
,
в каждой точке которого нарушается
единственность решения задачи Коши,
наз-ся особым решением этого ур-я. особые
решения не получаются из общего решения
ни при каких значениях параметраC.нахождение особого значения:1) Если![]() -
общее решение дифф. ур-я, то особое
решение находится из системы
-
общее решение дифф. ур-я, то особое
решение находится из системы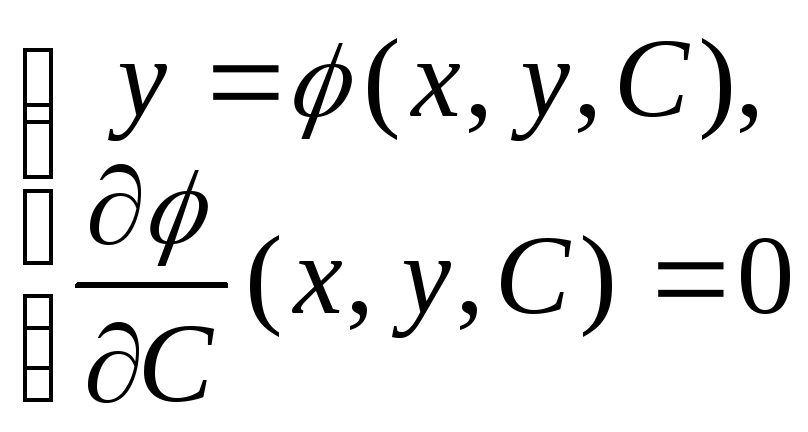 исключением
параметраC(причем надо
проверить, что это решение) 2) Если
Ф(x,C)=0 –
общий интеграл дифф. ур-я, то особое
решение находится из системы
исключением
параметраC(причем надо
проверить, что это решение) 2) Если
Ф(x,C)=0 –
общий интеграл дифф. ур-я, то особое
решение находится из системы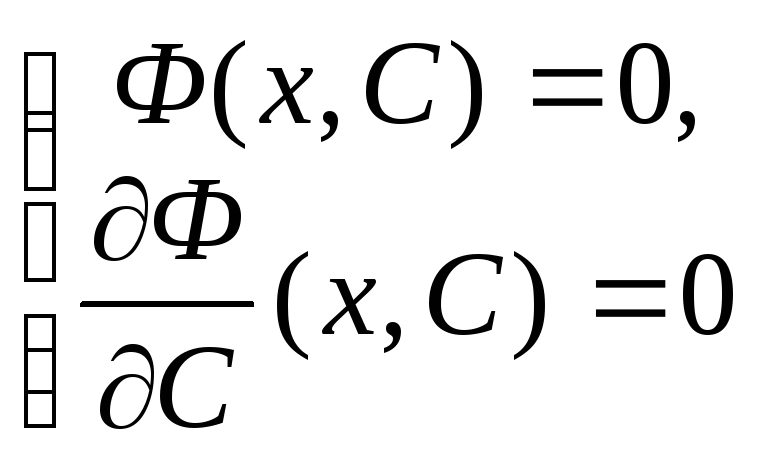 исключением параметраC(причем надо сделать проверку)
исключением параметраC(причем надо сделать проверку)
