1. Функція n змінних: Означення, область визначення, область значень, поверхні рівня. Границя функції в точці. Зв'язок границі функції в точці з повторними границями функції в точці. Зв'язок границі функції в точці з повторними границями функції в точці.

2. Неперервність функції n змінних в точці і замкненій області. Властивості неперервних в замкненій області функцій.

3.Поняття частинних похідних функції n змінних. Теорема про незалежність змішаних похідних від порядку диференціювання.

4.Диференційованість функції n змінних. Теорема про похідну складної функції.

5.Повний диференціал функції n змінних. Теорема про інваріантність форми першого диференціала. Застосування диференціалу до наближених обчислень.

6.Скалярне поле. Похідна за напрямом. Градієнт.

7.Локальні екстремуми функції 2-х змінних. Необхідна і достати а умови існування цих екстремумів (наслідок з формули Тейлора).

 Локальный экстремум функции двух переменныхНеобходимое условие локального экстремума дифференцируемой функции

     Если - точка экстремума функцииf, то

и или

     Достаточные условия локального экстремума дважды дифференцируемой функции

     Обозначим

     Если D > 0, A > 0, то - точка минимума.

     Если D > 0, A < 0, то - точка максимума.

     Если D < 0, экстемума в точке нет.

     Если D = 0, необходимы дополнительные исследования.

8.Локальні екстремуми функції n змінних. Необхідна і достатна умови існування. Критерій Сільвестра знаковизначенності квадратичної форми (без доведення).

Критерій Сільвестра знаковизначеності квадратичної форми.

Для того, щоби квадратична форма A(x,x), що задана у векторному просторі V, була додатно визначеною, необхідно і достатньо, щоб виконувались нерівності:.

Для того, щоби квадратична форма A(x,x), що задана у векторному просторі V, була від’ємно визначеною, необхідно і достатньо, щоб знаки кутових мінорів чергувались, при чому .

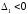9.Умовний екстремум функції n змінних. Дослідження функції на існування умовного екстремуму.

10.Подвійний інтеграл:

Означення, властивості, теорема існування, обчислення, застосування.

Означення

Застосуванння подвійного інтеграла:

Площа плоскої пластинки, маса плоскої пластинки,статистичні моменти пластинки , координати центра мас,моменти інерції пластинки.

Подвійним інтегралом від функції по області D називається межа, до якого прагне n-я інтегральна сума (*) при прагненні до нуля найбільшого діаметра часткових областей

Теорема Існування

Якщо функція неперервна в області D, обмеженої замкнутою лінією, то її n-я інтегральна сума прагне до межі при прагненні до нуля найбільшого діаметра часткових областей. Ця межа, тобто подвійний інтеграл, не залежить від способу розбиття області D на часткові області і від вибору в них точок Pi

11.Заміна змінних у подвійному інтегралі. Подвійний інтеграл в полярній системі координат.

12.Потрійний інтеграл:

Означення, властивості, умови існування, обчислення, застосування.

Застосування потрійного інтеграла: об*єм тіла, маса тіла, статистичні моменти тіла, координати центра мас, момент інерції.

13.Заміна змінної у потрійному інтегралі

14.Криволінійний інтеграл першого роду (по довжині дуги):

Означення, властивості, умови існування, обчислення, застосування.

Застосування криволінійного інтегралу: довжина дуги, маса розподілу вздовж кривої, статистичні моменти кривої, координати центра мас, моменти інерції.

15.Криволінійний інтеграл другого роду (по координатах):

Означення, властивості, умови існування, обчислення, застосування.

Застосування криволінійного інтегралу:робота, циркуляція площа.

16.Зв'язок між криволінійним інтегралом другого роду по замкнутому

контуру і подвійним інтегралом по області, яка обмежена цим контуром

(Формула Гріна).

Формула Грина

Пусть в плоскости Oxy задана область R, ограниченная замкнутой, кусочно-непрерывной и гладкой кривой C. Предположим, что в некоторой области, содержащей R, задана непрерывная векторная функция с непрерывными частными производными первого порядка . Тогда справедливаформула Грина где символ указывает, что кривая (контур)C является замкнутой, и обход при интегрировании вдоль этой кривой производится против часовой стрелки. Если , то формула Грина принимает вид где S − это площадь области R, ограниченной контуром C. Формулу Грина можно записать также в векторной форме. Для этого введем понятия ротора векторного поля. Пусть векторное поле описывается функцией Ротором или вихрем векторного поля называется вектор, обозначаемыйилии равный Формула Грина в векторной форме записывается в виде Заметим, что формула Грина вытекает из "теоремы Стокса" при переходе от трехмерног

17.Теорема про незалежність криволінійного інтеграла від форми шляху

З’ясуємо, за яких умов існує незалежність криволінійного інтеграла від вибору шляху інтегрування.

Визначимо області, з якими будемо мати справу.

Означення. Область називається однозв’язною, якщо для довільного замкненого контурамножина, обмежена, цілком міститься в ( замкнена без точок самоперетину неперервна кусково-гладка крива).

Якщо область однозв’язна, то довільний замкнений контур можна неперервно стягнути в точку, не виходячи з.

На рис. 50 а  показана однозв’язна область, а на рис. 50 б неоднозв’язна. Образно кажучи, однозв’язна областьце область без“дірок”.

 

 

Рис. 50 а                           Рис. 50 б

 

Теорема. Якщо в деякій замкненій однозв’язній області функціїівизначені і неперервні разом зі своїми частинними похіднимиі, то наступні чотири умови еквівалентні:

1) для довільних двох точок іобластікриволінійний інтеграл від заданих функцій не залежить від вибору шляху інтегрування, взятого в цій області;

2) криволінійний інтеграл по довільній замкненій кусково-гладкій кривій у даній області дорівнює нулю;

3) у даній області виконується умова

                                                        (77)

4) існує така функція , визначена в області, для якої виразє повним диференціалом, тобто

                                                  

Доведення. Доведення реалізуємо за схемою: .

Доведемо, що . Нехай в області, обмеженій замкненим контуром, виконуються умови теореми і умова 1). Нехайі  дві довільні криві, які належать області , сполучають точки і (рис. 51) і утворюють у сумі замкнену криву.

 

 

Рис. 51

 

Згідно з умовою

                                      

або

                                 

Оскільки , то

                                                   (78)

тобто умова 2) виконується.

Доведемо, що . Застосуємо теорему Гріна до лівої частини рівності (78). Маємо

                                  

Цей інтеграл дорівнює нулю тільки за умови

                                                     

звідки одержуємо (77), тобто умова 3) виконується.

Доведемо, що . Для заданих у теоремі функційізнайдемо функціюяка задовольняє рівностіі умову 3), тобтоТоді

                                            

Оскільки , то і, а це відповідає теоремі про рівність мішаних похідних для неперервно диференційовної в областіфункції. Оскільки, то

                                                   ,

тобто умова 4) виконується.

Доведемо, що . Якщо, аі  початкова і кінцева точки довільної кривої ( ), то

                            

18.Повний диференціал. Поповнення функції по її повному диференціалу