
- •Федеральное агентство по образованию РФ
- •АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
- •ТЕОРЕТИЧЕСКИЕ ОСНОВЫ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ НА ПЛОСКОСТИ
- •1.ПРОСТЕЙШИЕ ЗАДАЧИ НА ПЛОСКОСТИ
- •1.1. Расстояние между двумя точками
- •1.2. Деление отрезка в данном отношении
- •1.3. Площадь треугольника
- •2. ПРЯМАЯ ЛИНИЯ НА ПЛОСКОСТИ
- •2.1. Общее уравнение прямой
- •2.2. Каноническое уравнение прямой
- •2.3. Уравнение прямой, проходящей через две точки
- •2.5. Уравнение прямой в отрезках
- •2.6. Нормальное уравнение прямой
- •2.7. Расстояние от точки до прямой
- •2.8. Координаты точки пересечения двух прямых
- •2.9. Угол между двумя прямыми
- •2.11. Уравнение пучка прямых
- •3. КРИВЫЕ ВТОРОГО ПОРЯДКА
- •3.1. Эллипс
- •3.2. Окружность
- •3.3. Гипербола
- •3.4. Парабола
- •4. ПРЕОБРАЗОВАНИЯ КООРДИНАТ
- •4.1. Параллельный перенос
- •4.2. Поворот координатных осей
- •4.3. Изменение начала координат и поворот осей
- •5. ЛИНИИ В ПОЛЯРНОЙ СИСТЕМЕ КООРДИНАТ
- •5.1. Полярные координаты на плоскости
- •5.2. Связь полярных координат с декартовыми
- •5.3.1. Кривые второго порядка
- •5.3.2. Спирали
- •5.3.3. Розы
- •6. ПАРАМЕТРИЧЕСКОЕ ЗАДАНИЕ ЛИНИЙ
- •6.1. Окружность
- •6.2. Циклоида
- •6.3. Астроида
- •7. КРИВЫЕ ТРЕТЬЕГО ПОРЯДКА
- •7.1. Полукубическая парабола
- •7.2. Локон Аньези
- •7.3. Декартов лист
- •8. КРИВЫЕ ЧЕТВЕРТОГО ПОРЯДКА
- •8.1. Улитка Паскаля
- •8.2. Кардиоида
- •8.3. Лемниската Бернулли
- •Парабола
- •РЕШЕНИЕ ЗАДАЧ ПО АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ НА ПЛОСКОСТИ
- •ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
- •Вариант 1
- •ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
- •1. Поверхности
- •1.1. Линейчатые поверхности
- •1.2. Поверхности вращения
- •1.3. Поверхности второго порядка
- •2.1. Эллипсоид
- •2.2. Гиперболоиды
- •2.2.1. Однополостный гиперболоид
- •2.2.2. Двуполостный гиперболоид
- •2.3. Параболоиды
- •2.3.1. Эллиптический параболоид
- •2.4. Конус
- •2.5. Цилиндры
- •2.5.1. Эллиптический цилиндр
- •2.5.2. Гиперболический цилиндр
- •2.5.3. Параболический цилиндр
- •РЕШЕНИЕ ТИПИЧНЫХ ЗАДАЧ
- •ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
- •БИБЛИОГРАФИЧЕСКИЙ СПИСОК
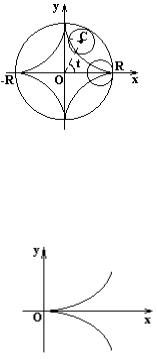
Пусть ox - прямая, по которой катится круг радиусом а. Тогда МС=СК=а, где К - точка касания.
За параметр t примем угол поворота МС относительно СК: t = MCK - угол качения (в радианах). Так как качение окружности происходит без скольжения,
то ОК= MK =at. Из рисунка видно, что
x = OP = OK − PK = OK − MQ = at − asin t = a(t −sin t), y = PM = KC −QC = a − acost = a(1−cost).
Таким образом, параметрические уравнения циклоиды
x = a(t −sin t), |
где − ∞ <t < ∞. |
y = a(1−cost), |
При 0 ≤t < 2π получаем первую арку циклоиды. Укажем, что длина дуги ОА1О1=8а, а площадь одной арки S=3 πa2.
6.3. Астроида
Астроидой называется кривая, которую описывает точка окружности радиуса R/4, когда окружность катится без скольжения внутри окружности радиуса R.
Параметрические уравнения астроиды
x = Rcos3 t,
y = Rsin3 t,
где 0 ≤t < 2π.
В декартовых координатах уравнение астроиды
x2/3+y2/3=R2/3.
Длина астроиды L=6R, а площадь, ограниченная астроидой S=3πR2/8.
7. КРИВЫЕ ТРЕТЬЕГО ПОРЯДКА
7.1. Полукубическая парабола
Уравнение полукубической параболы в декартовых координатах
a2 x3 − y2 = 0, a > 0.
Параметрические уравнения полукубической параболы:
x = t 2 |
, |
где − ∞ <t < ∞. |
|
|
|
y = at3 |
, |
|
24
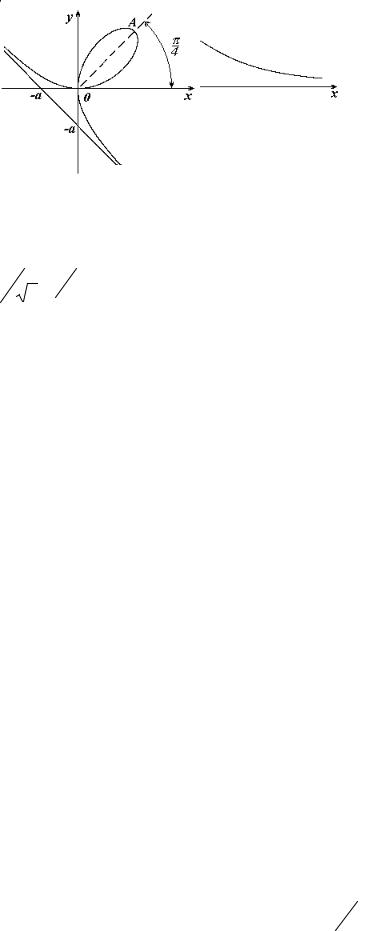
7.2. Локон Аньези
Уравнение локона Аньези в декартовых координатах:
|
|
|
x2 y = a2 (a − y) . |
||
Уравнение локона Аньези в полярных координатах: |
|||||
|
|
|
ρsin ϕ= |
a3 |
|
|
|
|
|
. |
|
|
|
|
a2 +ρ2 cosϕ |
||
Локон |
Аньези имеет асимптоту y = 0 при x → ±∞. Точки перегиба |
||||
(± a |
,3a |
4 |
) . |
|
|
3 |
|
|
|
|
|
Площадь между локоном Аньези и асимптотой S= πa2.
|
|
|
|
|
|
7.3. Декартов лист |
|
||||||||
|
|
Уравнения декартова листа в декартовых координатах |
|
||||||||||||
|
|
|
|
x3 + y3 = 3axy, |
a>0; |
|
|||||||||
в полярных координатах ρ = 3 a( |
|
sin 2ϕ |
|
) . |
|
|
|||||||||
sin3 ϕ+ cos3 ϕ |
|
||||||||||||||
|
|
2 |
|
|
|
|
|
||||||||
Параметрические уравнения декартова листа |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
3at |
|
|
|
|
|
|
|
|
|
|
|
|
x |
= |
|
|
|
, - ∞ < t < -1, |
|
|||||
|
|
1+t |
3 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3at 2 |
|
|
|
|
|
|||
|
|
|
|
y = |
|
|
, -1 < t < ∞. |
|
|||||||
|
|
1+t |
3 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
Декартов лист имеет асимптоту x+y+a=0 или ρ = |
. Точка |
||||||||||||
|
|
sinϕ + cosϕ |
|||||||||||||
A( |
3a |
, |
3a |
) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Площадь петли декартова листа S = 3a |
2 |
2 |
. |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
25
