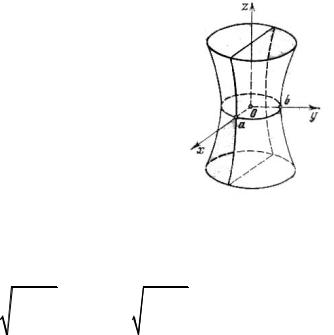
2.2.Гиперболоиды
2.2.1.Однополостный гиперболоид
Однополостным гиперболоидом называется по-
верхность второго порядка с каноническим уравнением
|
|
|
|
|
|
|
x2 |
|
+ |
y2 |
− |
z2 |
=1. |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
a2 |
b2 |
c2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
Линия |
пересечения |
|
гиперболоида |
и плоскости |
|
|
|
|
|||||||||||||||||||
z = 0 задается системой уравнений |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
y |
2 |
|
|
z |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
x |
|
+ |
|
− |
|
|
=1, |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
b2 |
c2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
a2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
= 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
определяющей эллипс с полуосями а и b. |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
В сечении плоскостью z = h имеем эллипс |
|
|
|
|
|
|
|
|||||||||||||||||||||
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
x |
|
+ |
y |
=1, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h2 |
|
|
|
|
h2 |
|
|
|
|
2 |
2 |
с полуосями a = a |
1+ |
и b =b |
1+ |
. |
|
|
|||||||||||||||||||||
a |
|
|
b |
c2 |
c2 |
|
|
|||||||||||||||||||||||
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
||||||
z = h, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
z |
2 |
|
|
|
|
|
Сечение поверхности S плоскостью |
x = 0 : |
|
y |
|
− |
|
=1, |
||||||||||||||||||||
|
|
|
|
|
c2 |
|||||||||||||||||||||||||
|
|
|
b2 |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 0 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|||
является гиперболой с действительной осью Oy и мнимой осью Oz . Сечение S плоскостью y = 0 - гипербола с действительной осью Ox и мнимой осью Oz .
При a = b получается однополостный гиперболоид вращения.
Покажем, что однополостный гиперболоид также является линейчатой
поверхностью, для чего перепишем уравнение в виде |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
x2 |
z2 |
|
|
|
|
|
y2 |
|
x |
|
|
|
|
z x |
|
|
z |
|
y |
|
|
|
y |
||||||||||||||||||||||||
|
|
|
− |
|
|
=1− |
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
+ |
|
|
|
|
|
= |
1− |
|
1+ |
|
|
. |
||||||||||||||
|
a |
2 |
c |
2 |
b |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
b |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
c a |
|
|
c |
|
b |
|
|
|
|
|||||||||||||||||||||
Рассмотрим две системы линейных уравнений: |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
x |
|
|
z |
|
|
|
|
|
|
y |
|
|
x |
|
z |
|
|
|
|
y |
|
|
|||||||||||||||||||||
|
|
|
|
v |
|
|
|
+ |
|
|
|
|
= u 1 |
+ |
|
|
|
|
|
, |
v |
|
|
|
|
|
+ |
|
|
|
= u 1 |
− |
|
|
|
, |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|||||||||||||||||||||||||||||||||
|
|
|
|
a |
|
|
c |
|
|
|
|
|
b |
|
a |
|
c |
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
x |
|
|
|
z |
|
|
|
|
|
y |
|
|
x |
|
z |
|
|
|
|
y |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
u |
|
− |
|
|
|
|
= v 1 |
− |
|
|
|
|
|
, |
|
u |
|
|
− |
|
|
|
= v 1 |
+ |
|
|
|
, |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
a c |
|
|
|
|
|
b |
|
|
a c |
|
|
|
|
b |
|
|
||||||||||||||||||||||||||||
где u и v |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
- |
параметры, |
не равные нулю. |
Каждая из этих систем определяет |
|||||||||||||||||||||||||||||||||||||||||||||
прямую (линию пересечения двух плоскостей). Если перемножить уравнения каждой системы, получится уравнение однополостного гиперболоида, откуда следует, что каждая из этих прямых целиком лежит на однополостном гиперболоиде. Таким образом, через каждую точку однополостного гиперболоида проходят две прямые, называемые прямолинейными образующими однополостного гиперболоида, он имеет два семейства прямолинейных
69