
- •Федеральное агентство по образованию РФ
- •АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
- •ТЕОРЕТИЧЕСКИЕ ОСНОВЫ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ НА ПЛОСКОСТИ
- •1.ПРОСТЕЙШИЕ ЗАДАЧИ НА ПЛОСКОСТИ
- •1.1. Расстояние между двумя точками
- •1.2. Деление отрезка в данном отношении
- •1.3. Площадь треугольника
- •2. ПРЯМАЯ ЛИНИЯ НА ПЛОСКОСТИ
- •2.1. Общее уравнение прямой
- •2.2. Каноническое уравнение прямой
- •2.3. Уравнение прямой, проходящей через две точки
- •2.5. Уравнение прямой в отрезках
- •2.6. Нормальное уравнение прямой
- •2.7. Расстояние от точки до прямой
- •2.8. Координаты точки пересечения двух прямых
- •2.9. Угол между двумя прямыми
- •2.11. Уравнение пучка прямых
- •3. КРИВЫЕ ВТОРОГО ПОРЯДКА
- •3.1. Эллипс
- •3.2. Окружность
- •3.3. Гипербола
- •3.4. Парабола
- •4. ПРЕОБРАЗОВАНИЯ КООРДИНАТ
- •4.1. Параллельный перенос
- •4.2. Поворот координатных осей
- •4.3. Изменение начала координат и поворот осей
- •5. ЛИНИИ В ПОЛЯРНОЙ СИСТЕМЕ КООРДИНАТ
- •5.1. Полярные координаты на плоскости
- •5.2. Связь полярных координат с декартовыми
- •5.3.1. Кривые второго порядка
- •5.3.2. Спирали
- •5.3.3. Розы
- •6. ПАРАМЕТРИЧЕСКОЕ ЗАДАНИЕ ЛИНИЙ
- •6.1. Окружность
- •6.2. Циклоида
- •6.3. Астроида
- •7. КРИВЫЕ ТРЕТЬЕГО ПОРЯДКА
- •7.1. Полукубическая парабола
- •7.2. Локон Аньези
- •7.3. Декартов лист
- •8. КРИВЫЕ ЧЕТВЕРТОГО ПОРЯДКА
- •8.1. Улитка Паскаля
- •8.2. Кардиоида
- •8.3. Лемниската Бернулли
- •Парабола
- •РЕШЕНИЕ ЗАДАЧ ПО АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ НА ПЛОСКОСТИ
- •ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
- •Вариант 1
- •ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
- •1. Поверхности
- •1.1. Линейчатые поверхности
- •1.2. Поверхности вращения
- •1.3. Поверхности второго порядка
- •2.1. Эллипсоид
- •2.2. Гиперболоиды
- •2.2.1. Однополостный гиперболоид
- •2.2.2. Двуполостный гиперболоид
- •2.3. Параболоиды
- •2.3.1. Эллиптический параболоид
- •2.4. Конус
- •2.5. Цилиндры
- •2.5.1. Эллиптический цилиндр
- •2.5.2. Гиперболический цилиндр
- •2.5.3. Параболический цилиндр
- •РЕШЕНИЕ ТИПИЧНЫХ ЗАДАЧ
- •ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
- •БИБЛИОГРАФИЧЕСКИЙ СПИСОК

РЕШЕНИЕ ЗАДАЧ ПО АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ НА ПЛОСКОСТИ
Задача 1. Определить элементы треугольника, если заданы уравнения трех его сторон:
АС: х – 2у + 5 = 0, АВ: х + 2у – 3 = 0,
ВС: 2х + у – 15 = 0.
Решение
1. Вершины треугольника
Координаты вершин треугольника находятся как точки пересечения соответствующих сторон. Так, например, координаты точки А являются решением системы уравнений
x − 2y +5 = 0,
x + 2y −3 = 0.
Нетрудно показать, что А (-1, 2). Аналогично находим В (9, -3) и С (5, 5).
2. Уравнения высот
Высотой треугольника называется отрезок перпендикуляра, опущенного из вершины треугольника на противоположную сторону.
Так, например, hc = CC1 AB. Уравнение высоты СС1 ищем как уравнение
прямой у |
= |
k1x + b, если известен угловой коэффициент прямой АВ: |
|||||
y = − |
1 x + |
3 |
, |
равный k2 |
= − |
1 |
. Из условия перпендикулярности прямых k1 k2 |
|
2 |
2 |
|
|
|
2 |
|
= -1 → k1 = 2. Поскольку высота СС1 проходит через точку (5, 5), уравнение hc имеет вид у – 5 = 2 (х – 5) или у = 2х – 5.
Анализ уравнений сторон АС: y = 12 x + 52 и ВС: у = -2х + 5 убеждает нас в том, что АС ВС, и треугольник является прямоугольным. Таким образом, hA: y = 12 x + 52 ; hB: у = -2х + 15.
3. Уравнения медиан
Медианой называется отрезок прямой, соединяющей вершину треугольника с серединой противолежащей ей стороны.
Координаты середин сторон находятся по формулам деления отрезка в данном отношении (см. п.1.2): С2 (4, -1/2), В2 (2, 7/2), А2 (7, 1).
Уравнение медианы mC = CC2 получается как уравнение прямой, проходящей через точки С и С2 (см. п.2.3):
y −5 |
= |
x |
−5 |
или mC: 11х – 2у – 45 = 0. |
−1 2 −5 |
|
−5 |
||
4 |
|
|||
34

Аналогично mВ: -13х – 14у + 75 = 0, mА: -x – 8y + 15 = 0.
4. Длины сторон
По формуле расстояния между двумя точками (см. п.I.I):
AB = c = 102 +52 = 5 5, BC = a = 4 5, AC = b = 3 5.
5. Уравнения биссектрис
Биссектрисой треугольника называется лежащий в треугольнике отрезок прямой, которая делит его внутренний угол пополам.
Укажем два способа нахождения уравнения биссектрисы треугольника.
а). Биссектриса делит противолежащую сторону в отношении, пропорциональном прилежащим сторонам.
Если С3 – точка пересечения биссектрисы lC = CC3 со стороной АС, то
АС3 = АС = b = 3 . С3 В СВ a 4
Координаты точки С3 находим по формулам деления отрезка в данном отношении λ = 3/4 (см. п.1.2): С3 (23/7, -1/7).
Уравнение биссектрисы lC = CC3 получается как уравнение прямой, проходящей через точки С3 и С (5, 5) (см. п.2.3):
y −5 |
|
= |
x −5 |
|
или 3х – у – 10 = 0. |
|
−1 7 − |
5 |
23 7 − |
5 |
|||
|
|
б). Уравнение биссектрисы lC = CC3 может быть найдено из условия того, что точки биссектрисы CC3 равноудалены от сторон АС и СВ.
Вычислим отклонения точки (х, у), лежащей на биссектрисе, от сторон АС
и СВ (см. п.2.7): |
|
|
|
|
||
δАС = |
x −2y +5 |
, |
δСB = |
2x + y −15 |
; |
|
− 5 |
5 |
|||||
|
|
|
|
|||
δАС и δСВ отрицательны, так как начало координат и точки биссектрисы треугольника лежат по одну сторону от сторон АС и СВ. Учитывая, что d = |δ|, уравнение биссектрисы получим из равенства δ = −δ , δ < 0 ,-δАС = -δСВ,
которое принимает вид: |
x − 2y +5 |
= − |
2x + y −15 |
или lC: 3х – у – 10 = 0. |
|
5 |
5 |
||||
|
|
|
Для вычисления биссектрисы угла А lА применим второй способ.
Отклонение δАС = − x − 2y +5
 5
5
биссектриса lА лежат по одну сторону от стороны АС.
Отклонение δAB = x + 2y −3
 5
5
биссектриса lА лежат по разные стороны от стороны АВ. Для биссектрисы lА справедливо -δАС = δАВ,
35
то есть |
x − 2y +5 |
= x + 2y −3 |
или х – 2у + 5 = х + 2у –3. |
|
5 |
||||
|
5 |
|
||
Следовательно, 4у = 8. Таким образом, lА: у = 2. |
||||
Уравнение lВ: х+у – 6 = 0 может быть найдено одним из двух способов.
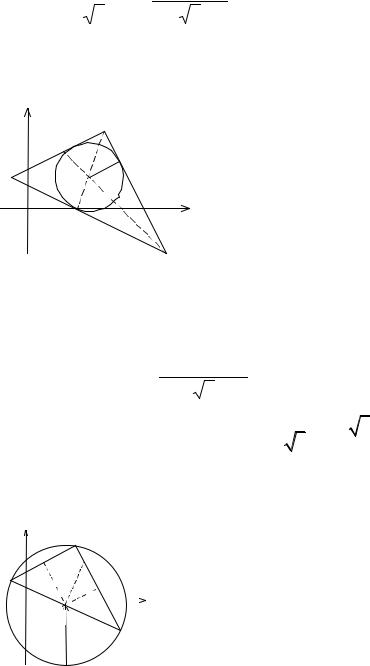
6. Центр и радиус вписанной окружности |
|
|||||||
|
у |
Биссектрисы треугольника пересекаются в |
||||||
|
|
|
|
|
С |
одной точке, являющейся центром вписанной |
||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
окружности. |
|
|
|
|
|
|
|
r |
|
|
|
А |
|
|
|
|
|
|
Система уравнений, составленная из уравнений |
|
|
|
01 |
|
|
х |
|||
|
|
|
|
|
||||
|
0 |
|
|
|
биссектрис: |
|
||
|
|
|
|
|
3х− у−10 |
= 0, |
||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
у = 2, |
|
имеет решение х = 4, у = 2.
Следовательно, центр вписанной окружности находится в точке О1 (4, 2). Радиус вписанной окружности найдем как расстояние от точки О1 до
стороны АС: δ |
АС |
|
= − x0 −2y0 |
+5 , где х = 4, у = 2. |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
5 |
|
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Таким образом, |
r = dAC = |
|
δAC |
|
|
= |
|
− 4 − 4 +5 |
|
|
= |
5. |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
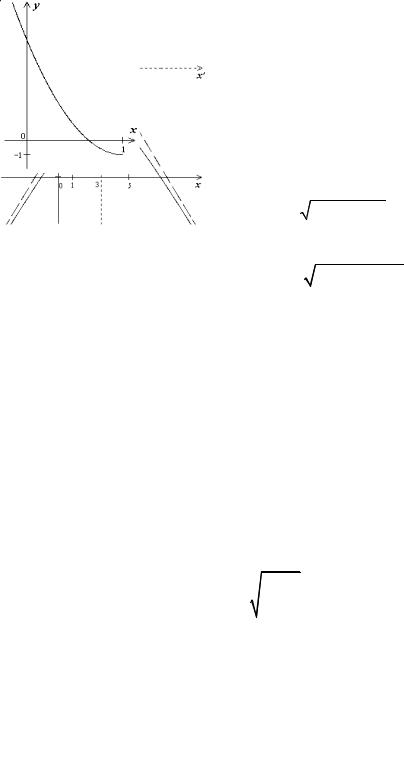
7. Центр и радиус описанной окружности |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
Центр описанной |
окружности |
находится |
в |
точке |
пересечения |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
перпендикуляров, |
восстановленных |
|
к |
сторонам |
|||||||||||||||||
|
у |
|
С |
|
|
|
|
треугольника в их серединах. |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
BB2 |
|
|
|
|
Координаты |
середин |
сторон |
|
АС |
и |
АВ |
|
найдены |
|||||||||||||||
|
А |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х в п.3). |
С2 (4, -1/2), В2 (2, 7/2). |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
A2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
Уравнения линий серединных перпендикуляров hC |
|
и hB |
|||||||||||||||||||
|
O0 |
O2 |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
R |
|
|
B |
|
находим аналогично вычислениям в п.2. |
|
|
|
2 |
2 |
|||||||||||||||||
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
Угловые |
коэффициенты |
hC |
2 |
и hB |
равны |
|
2 |
и -2 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
соответственно, и эти прямые проходят через точки С2 и В2, их уравнения имеют вид:
|
h |
|
: y + |
1 |
|
= 2(x −4) |
или 4x −2y −17 = 0, |
|
|
|
|
|
|||||
|
C2 |
2 |
|
|
||||
|
|
|
|
|
||||
|
h |
|
: y − |
7 |
|
= −2(x −4) |
или 4x + 2y −15 = 0. |
|
|
|
|
||||||
|
B |
2 |
|
|
|
|||
|
|
2 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
Система уравнений, составленная из уравнений серединных |
||||||||
перпендикуляров: |
|
|
|
|
|
|
|
|
4x − 2 y −17 = 0, |
, имеет решение х = 4, у = -1/2. |
|||||||
|
|
0 |
||||||
4x + 2 y −15 |
= |
|
|
|
|
|
|
|
36

Следовательно, центр описанной окружности находится в точке О2 (4, -1/2). Нетрудно заметить, что центр описанной окружности совпал с серединой
стороны АВ: R = 12 AB = 5 25 .
8. Центр тяжести треугольника Центр тяжести треугольника находится в точке пересечения медиан.
Из п.3 имеем систему уравнений для определения координат центра
11x − 2y − 45 = 0,
тяжести
−13x −14y + 75 = 0.
Система имеет решение х = 4,33, у = 1,3. Следовательно, центр тяжести
треугольника находится в точке О3 (4,33; 1,3). |
|
|
|
|
|
|
|
|
|
||||||||
|
Укажем, что медианы треугольника делятся точкой пересечения в |
||||||||||||||||
отношении 2 : 1, считая от вершины. |
|
|
|
|
|
|
|
|
|
|
|||||||
|
Таким образом, координаты центра тяжести могут быть найдены как |
||||||||||||||||
координаты точки О3, делящей медиану в отношении λ = |
СО3 |
= |
2 |
. |
|||||||||||||
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
С С |
2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
||
|
Если воспользоваться формулами деления отрезка в данном отношении |
||||||||||||||||
(см. п.1.2), то координаты точки: |
|
|
|
|
|
|
|
|
|
|
|
||||||
x |
= |
xC + 2xC |
2 |
= |
5 + 2 4 |
= 4,33; |
y = |
yC + 2yC |
2 |
= |
5 + 2 (−1 2) |
=1,33. |
|||||
|
|
|
|
|
|
|
|
|
|||||||||
O |
|
3 |
|
|
3 |
|
O |
3 |
|
|
3 |
|
|
|
|
|
|
3 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
9. |
Внутренние углы треугольника |
|
|
|
|
|
|
|
|
|
|
|
|||||
Внутренние углы треугольника могут быть найдены через угловые коэффициенты прилежащих сторон. Например, внутренний угол при
вершине А треугольника tgA = |
|
|
kAC − kAB |
= |
|
1 2 −(−1 2) |
= 4 . |
1 |
+ kAC kAB |
|
|||||
|
|
1+1 2 (−1 2) 3 |
|||||
Следовательно, А = arctg(4/3). 10. Площадь треугольника
По формуле площади треугольника (см. п.1.3) имеем
S∆ = |
1 |
|
−1 |
2 |
1 |
|
|
|
1 |
|
|
||
|
|
|
|
|
|||||||||
|
9 −3 |
1 |
|
= |
60 = 30 (кв. ед.). |
||||||||
|
|
||||||||||||
2 |
|
5 |
|
5 |
1 |
|
|
2 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||
Площадь треугольника может быть вычислена по формуле |
|||||||||||||
S∆ = p r, |
где p – полупериметр треугольника; |
||||||||||||
|
|
|
|
r – радиус вписанной окружности. |
|||||||||
Поскольку p = |
3 |
5 +5 |
|
|
5 + 4 5 |
= 6 5, a r = 5, то S∆ =30 (кв. ед.). |
|||||||
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
5 |
|
|
|
||||
Задача 2. Найти точки пересечения следующих линий: |
|||||||||||||
2.1. (x – 1)2 + (y – 3)2 = 4 |
и (x – 3)2 + (y – 5)2 = 4; |
||||||||||||
37

2.2. (x – 5)2 + y2 = 1 |
|
и x + y = 0. |
||||||||||||
Решение |
|
|
|
|
|
|
|
|
|
|
|
|
||
1. x2 |
+ y2 |
− 2x − 6y + 6 = 0, |
вычитая из первого уравнения второе, |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x2 |
+ y2 |
−6x −10y |
|
+30 = 0, |
|
|||||||||
|
|
|
|
|
|
2 |
+ y |
2 |
− 2x − 6y + 6 = 0, |
|||||
получим систему x |
|
|
||||||||||||
|
|
|
y = −x + 6, |
|
||||||||||
решая которую, получаем две точки пересечения (1, 5) и (3, 3). |
||||||||||||||
2.2. Линии |
(x – 5)2 |
|
+ y2 |
= 1 и x + y = 0 не пересекаются, так как система |
||||||||||
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
уравнений (х−5) |
+ |
у |
=1, не имеет действительных решений. |
|||||||||||
|
|
|||||||||||||
|
|
|
х+ у = 0 |
|
|
|
|
|
|
|||||
Задача 3. Найти проекцию точки Р (4, 9) на прямую, проходящую через точки
А (3, 1) и В (5, 2).
Решение
Искомую точку найдем, решая совместно уравнение прямой АВ с уравнением перпендикуляра, проведенного к этой прямой из точки Р.
АВ: |
|
х−3 |
= |
у −1 |
→ у = |
1 |
х− |
1 |
. |
|
|
|
|
||||
|
|
1 |
|
2 |
2 |
|
|
|
|
||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||
Уравнение |
|
|
перпендикуляра |
|
из |
точки Р на прямую АВ |
ищем в виде |
||||||||||
у – 9 = k(x – 4); из условия перпендикулярности k |
1 |
= −1 |
→ k |
= −2. |
|||||||||||||
|
1 |
|
1 |
|
|
|
|
|
|
|
|
2 |
|
|
|
||
x − |
, |
|
|
x = 7, |
|
|
|
|
|
|
|
|
|||||
y = |
2 |
2 |
→ |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
y = 3. |
|
|
|
|
|
|
|
|
y = −2x +17, |
|
|
|
|
|
|
|
|
|
|
|
||||||
Задача 4. Постройте прямую 3х – 5у + 15 = 0.
Решение
|
у |
|
3 |
|
х |
-5 |
0 |
Уравнение прямой в отрезках имеет вид: −x5 + 3y =1,
прямая отсекает на осях отрезки (-5) и 3.
Задача 5. Даны две прямые 2х + 3у – 5 = 0, 7х +15у +1 = 0, пересекающиеся в точке М. Составить уравнение прямой, которая проходит через точку М и перпендикулярна к прямой 12х – 5у – 1 = 0.
Решение
Прямые пересекаются, так как угловые коэффициенты 2/7 ≠ 3/15. Составим уравнение пучка прямых с центром в точке М (см. п.2.11):
2х + 3у – 5 + λ (7х + 15у +1) = 0.
38

Чтобы выделить в этом пучке искомую прямую, найдем ее из условия перпендикулярности к прямой 12х – 5у – 1, для которой k1 = 12/5.
Из уравнения пучка прямых |
(2 + 7λ) х + (3 + 15λ) у + (-5 + λ) = 0 получаем |
|||||||||
k = − |
2 + 7λ |
= − |
1 |
, значит, − |
2 + 7λ |
= − |
|
5 |
, откуда λ = -1 и уравнение искомой |
|
3 +15λ |
k |
3 +15λ |
12 |
|||||||
|
|
|
|
|
||||||
|
|
|
1 |
|
|
|
|
|
|
|
прямой:
5х + 12у + 6 = 0.
Задача 6. Написать уравнение прямой L, проходящей через точку М (2, 1) под углом 45° к прямой L1: 2х + 3у +4 = 0.
Решение
Угол между прямыми найдем из выражения для тангенса угла α между
ними (см. п.2.9): |
|
|
||||
tgα = |
|
|
k + 2 3 |
|
=1, где k – угловой коэффициент искомой прямой. |
|
1 |
−(2 3) k |
|||||
|
|
|
||||
Из этого уравнения k1 = 1/5, k2 = -5.
Используя координаты точки М, запишем уравнения искомых прямых:
|
1 |
3 |
|
|
|
x −5y +3 = 0, |
L : y = |
5 x + |
5 |
, |
или |
|
|
|
|
|
|
|
|
5x + y −11 = 0. |
y = −5x +11 |
|
|
||||
Задача |
7. |
Составить |
L1: х + 2у – 1 = 0 и L2: х + |
||
1 |
y |
|
|
|
|
L |
|
|
L |
|
x |
2 |
0 |
|
L |
|
|
|
|
M(x,y) |
Решение |
|
|
уравнение прямой L, параллельной прямым 2у +2 = 0 и проходящей посередине между ними.
1 способ. Уравнение прямой L будем искать в виде А(х – х0) + В(у + у0) = 0. В
качестве нормального вектора |
n ={A, B} можно выбрать нормальный вектор |
|
прямых |
L1 и L2, равный |
{1, 2}. Найдем какую-нибудь точку |
М0 (х0, у0) |
L. Точка М0 будет делить пополам отрезок, соединяющий две |
|
любые точки, лежащие на L1 и L2. Например, М1 (1, 0) L1 и М2 (-2, 0) L2, тогда точка М0 имеет координаты (-1/2, 0), и уравнение прямой L принимает
вид: х + 2у + 1/2 = 0.
2 способ. Произвольная точка М (х, у) L, если (см. п.2.6)
| δ (М, L1) | = | δ (М, L2) |.
Для снятия модуля определим знаки отклонений точки М (х, у) от прямых L1 и L2. Для этого нужно выяснить взаимное расположение начала координат, точки М (х, у) и прямых L1 и L2.
39

Приведем уравнения прямых к нормальному виду:
L1 |
|
1 |
|
x + |
2 |
|
y − |
1 |
|
|
n1 |
|
1 |
|
|
|
|
2 |
|
|
|||||
: |
|
|
|
|
|
|
|
|
|
= 0, |
= |
|
|
|
, |
|
|
, |
|||||||
5 |
|
5 |
5 |
|
|
5 |
|
|
5 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
L2 |
: − |
1 |
|
x − |
2 |
|
y − |
1 |
|
= 0, |
n2 |
|
−1 |
, |
−2 |
|
, |
||||||||
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
||||||||||
5 |
5 |
|
5 |
5 |
|
5 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
где n1 и n2 - единичные векторы нормалей к прямым L1 и L2, проведенным из
начала координат.
Видим, что n1 и n2 противоположны по направлению, значит, начало координат
лежит в полосе между прямыми L1 и L2. Отсюда заключаем, что точка М и начало координат лежат по одну сторону как от прямой L1, так и от прямой L2, значит, отклонения точки М от прямых L1 и L2 имеют один и тот же знак
|
x + 2y −1 |
|
−x − 2y − 2 |
|
следует |
|||
(отрицательный), тогда из |
|
= |
|
|||||
5 |
|
5 |
||||||
|
|
|
|
|
|
|||
х + 2у – 1 = -х – 2у – 2 и |
х + 2у + 1/2 = 0. |
|
|
|||||
Задача 8. Составить уравнение эллипса, фокусы которого лежат на оси абсцисс, симметрично относительно начала координат, зная, что малая ось равна 10, а эксцентриситет равен 12/13.
Решение |
|
|
|
|
|
b = 5, е = 12/13. Поскольку е = с/а и а2 = b2 + c2, то |
||||||||||
|
|
Из условия имеем |
||||||||||||||
|
2 |
|
2 |
2 |
2 |
|
|
2 |
|
b2 |
|
|
|
|
|
|
a |
|
= b |
|
+ е a |
|
или |
a |
|
= |
|
. Подставляя числовые значения, получим |
|||||
|
|
|
|
1−e2 |
||||||||||||
|
|
а2 = 169. |
|
|
|
|
|
|
|
х2 |
|
у2 |
|
|||
|
|
Следовательно, уравнение эллипса имеет вид: |
|
+ |
=1. |
|||||||||||
|
|
169 |
25 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Задача 9. Составить уравнение эллипса, фокусы которого лежат на оси абсцисс, симметрично относительно начала координат, зная, что его большая ось равна 10, а расстояние между фокусами равно 8.
Решение
Из условия имеем а = 5, с = 4. Вычислим малую полуось b = a2 −c2 = 25 −16 = 3.
Следовательно, уравнение эллипса имеет вид: х2 + у2 =1. 25 9
Задача 10. Фокусы гиперболы совпадают с фокусами эллипса
Составить уравнение гиперболы, если ее эксцентриситет равен 2.
Решение
Из уравнения эллипса находим: aэл.2 = 25, bэл.2 = 9.
сэл.2 = aэл.2 - bэл.2 = 16, сэл. = 4. По условию сгип. = сэл. = с и егип. = с/агип. = 2.
x2 + y2 =1. 25 9
40
Таким образом, агип. = с/2 = 2 и bгип.2 = с2 – агип.2 = 16 |
– 4 = 12. |
||||
Уравнение искомой гиперболы имеет вид: |
x2 |
− |
y2 |
=1. |
|
4 |
12 |
|
|||
|
|
|
|
||
Задача 11. Составить уравнение параболы, если известны ее фокус F(-7, 0) и уравнение директрисы x – 7 = 0.
Решение
Из уравнения директрисы имеем x = -p/2 = 7 или p = -14.
Таким образом, уравнение искомой параболы y2 = -28x.
Задача 12. Установить, какие линии определяются следующими уравнениями. Сделать чертежи.
1. y = 7 − |
3 |
|
x2 −6x +13, y < 7, x R. |
|
|
|
|
|
|
||||
2 |
|
|
|
|
|
|
Решение |
|
|
|
|
||
y −7 = − 3 |
x2 −6x +13. |
Возводим |
обе |
части |
||
2 |
|
|
|
|
||
уравнения в квадрат: |
|
|
|
|||
|
|
|
(y −7)2 = 94 (x2 −6x +13) |
или |
|
|
|
|
|
4 (y −7)2 =(x2 −6x +13). |
|
||
|
|
|
9 |
|
|
|
Выделяем в правой части полный квадрат: |
|
|||||
4 (y −7)2 = (x −3)2 + 4 или |
(x −3)2 − ( y −7)2 |
= −1. |
||||
9 |
|
|
|
4 |
9 |
|
Это – сопряженная гипербола. О′(3, 7), полуоси а = 2, b = 3.
Заданное же уравнение определяет ветвь гиперболы, расположенную под прямой y – 7 = 0, т.к. y < 7.
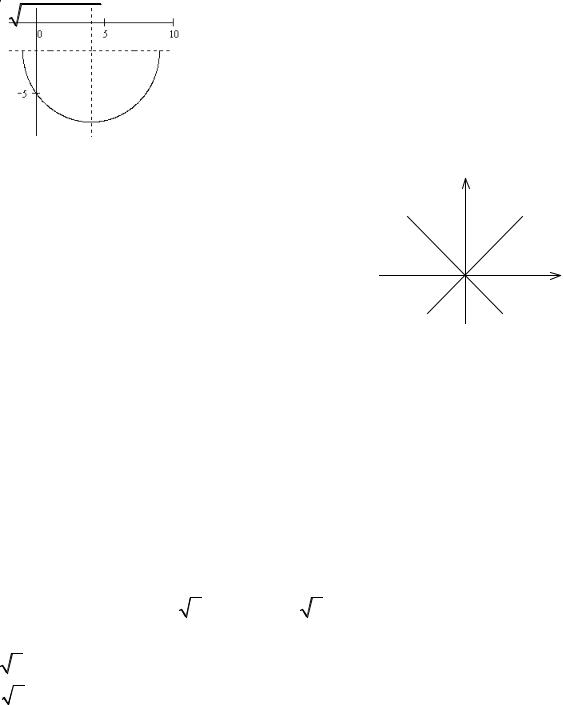
2. |
x =1− |
1 |
y +1 |
. |
|
2 |
2 |
||||
|
|
|
Решение
Область допустимых значений (х, у) определяется
условиями |
|
|
|
|||
y +1 |
≥ 0, |
|
y ≥ −1, |
|||
|
|
|
|
→ |
||
|
2 |
|
||||
|
|
|
|
|||
|
− x |
≥ 0, |
|
x ≤1. |
||
1 |
|
|
||||
(y + 1)/2 = 4 (1 – x)2 → y + 1 = 8 (1 – x)2.
Искомая кривая – часть параболы с вершиной в точке (1, -1).
41
3. y = −2 − 9 − x2 +8x.
Решение
Искомая кривая – часть окружности:
(y + 2)2 + (x – 4)2 = 52, y ≤ -2, x [-1, 9].
4. y2 – x2 = 0. |
|
|
y |
|
Решение |
|
|
||
(y – x) (y + x) = 0 |
y=-x |
y=x |
||
|
||||
|
|
|
– две пересекающиеся прямые.
x
0
Задача 13. Какую линию определяет уравнение x2 + y2 = x?
Решение
Запишем уравнение в виде x2 – x + y2 = 0.
Выделим полный квадрат из слагаемых, содержащих х: x2 – x = (x – 1/2)2 – 1/4.
|
1 |
2 |
2 |
= |
1 |
|
Уравнение принимает вид x − |
2 |
|
+ y |
|
4 |
|
|
|
|
|
|
||
и определяет окружность с центром в точке (1/2, 0) и радиусом 1/2.
Задача 14. Преобразовать уравнение x2 – y2 = a2 поворотом осей на 45° против часовой стрелки.
Решение
Так как α = -45°, то cosα = 2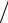 2, sin α = − 2
2, sin α = − 2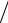 2.
2.
Отсюда преобразование поворота принимает вид (см. п.4.2):
x = 2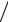 2 (x′+ y′),
2 (x′+ y′),
y = 2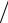 2 (y′− x′).
2 (y′− x′).
Подстановка в исходное уравнение дает х′у′= а2/2.
Проиллюстрируем приведение общих уравнений прямых второго порядка к каноническому виду на нескольких примерах, иллюстрирующих разные схемы преобразований.
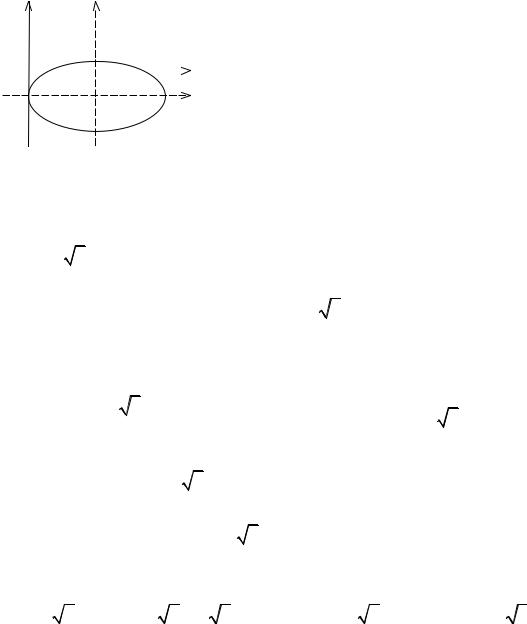
Задача 15. Привести уравнение 5x2 + 9y2 – 30x + 18y + 9 = 0 к каноническому виду и построить кривую.
Решение
Сгруппируем члены этого уравнения, содержащие одноименные
координаты:
(5x2 – 30x) + (9y2 + 18y) +9 = 0, или 5(x2 – 6x) + 9(y2 + 2y) +9 = 0.
42
|
|
y |
|
|
|
|
|
y′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дополняем члены в скобках до полных квадратов: |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
5(x2 – 6x + 9 – 9) + 9(y2 + 2y + 1 – 1) +9 = 0, или |
|||||||||||||||||||||||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5(x – 3)2 + 9(y + 1)2 = 45. |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
01 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Обозначаем x′= x – 3, y′= y + 1, |
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x0 = 3, y0 = -1, то есть точка О1(3, -1) – центр |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
кривой. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Уравнение в новой системе координат принимает |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′2 |
|
|
|
y |
′2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
′2 |
|
+9y |
′2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
= |
45 → |
|
|
9 |
|
+ |
|
|
5 =1 |
|
|
и |
определяет |
|
|
эллипс |
|
с |
|
полуосями |
||||||||||||||||||||||||||||||||||||||
5x |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
а = 3, b = 5,который в исходной системе координат имеет центр в точке |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
О1(3, -1). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Задача 16. Определить вид кривой |
5 x2 |
+ |
|
3 |
|
xy |
+ |
7 y2 |
= 2. |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
Решение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
Определим угол поворота осей по формуле (7) п.4.4: |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
A = |
5 |
,C |
|
7 |
, B = |
|
3 |
|
, A ≠ C иϕ= |
1 |
arctg |
|
2B |
1 |
arctg (− |
|
3)= − |
π |
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
= |
|
|
|
|
|
|
|
|
|
= |
|
|
6 . |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
4 |
4 |
|
4 |
|
2 |
A −C |
2 |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
Подвергнем уравнение кривой преобразованию: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
′ |
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
′ |
|
|
3 |
|
|
+ y |
′ |
1 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
x = x cosϕ− y |
|
sin ϕ= x |
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′1 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
′ |
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
+ y |
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
y = x sin ϕ+ y |
|
cosϕ= −x |
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
и получим уравнение эллипса |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
5 |
′ |
|
3 |
|
+ y |
′1 |
2 |
|
|
3 |
|
|
|
′ |
3 |
|
+ y |
′ |
1 |
|
|
1 |
′ |
|
3 |
′ |
|
|
7 |
|
|
1 |
′ |
|
|
3 |
′ |
2 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
+ |
|
|
− |
|
|
|
|
= 2 . |
||||||||||||||||||||||||
|
|
|
4 |
x |
2 |
|
|
|
2 |
2 |
|
|
x |
|
|
2 |
|
|
|
2 |
2 |
x + |
2 |
|
y |
4 |
2 |
x + |
2 |
y |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
x′2 + 2y′2 = 2.
Задача 17. Установить, какую линию определяет уравнение x2 + y2 + xy – 2x + 3y = 0.
Решение
Перенесем начало координат в такую точку О1(х0, у0), чтобы уравнение не содержало х′ и у′ в первой степени.
Это соответствует преобразованию координат вида (см. п.4.1):
x = x′+ x0 ,y = y′+ y0.
Подстановка в исходное уравнение дает
(x′+ x0)2 + (x′+ x0)(y′+ y0) + (y′+ y0)2 – 2(x′+ x0) + 3(y′+ y0) = 0 или
x′2 + x′y′+ y′2 + (2x0 + y0 - 2)x′+ (x0 + 2y0 + 3)y′+ x02 + x0y0 + y02 - 2x0 + 3y0 =0.
Положим 2x0 + y0 – 2 = 0, x0 + 2y0 + 3 = 0.
43
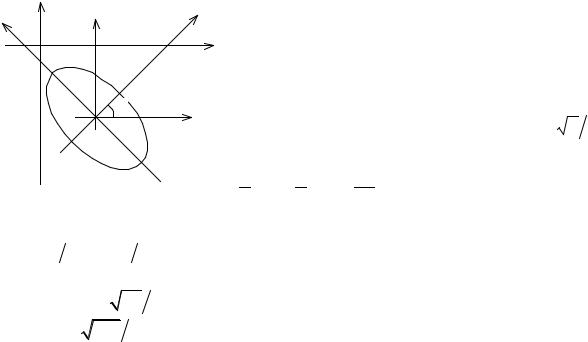
Решение полученной системы уравнений: x0 = 7/3 и y0 = -8/3. |
|
|
|
|
|||||||||||
|
Таким образом, координаты нового начала координат O1(7/3, -8/3), а |
||||||||||||||
уравнение принимает вид x′2 + x′y′+ y′2 = 93/25. |
|
|
|
|
|||||||||||
|
Повернем оси координат на такой угол α, чтобы исчез член х′у′. |
|
|
|
|||||||||||
|
Подвергнем последнее уравнение преобразованию (см. п.4.2): |
|
|
|
|
||||||||||
|
x′ = x′′cosα − y′′sin α, |
|
|
|
|
|
|
|
|
|
|||||
|
|
′ |
′′ |
|
′′ |
cosα |
|
|
|
|
|
|
|
|
|
|
y |
|
= x sin α+ y |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
и получим (cos2α + sinα cosα + sin2α) x′′2 |
+ |
||||||||
y′′ |
y |
′ |
|
x′′ |
(cos2α - sin2α) x′′y′′+ |
|
|
|
|
||||||
|
y |
|
|
|
x |
|
|
|
|
2 |
2 |
|
2 |
|
|
|
0 |
|
|
|
|
|
|
+ |
|
(sin α - sinα cosα + |
cos α) y′′ |
|
= |
||
|
|
|
|
|
93/25. |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
Полагая cos2α - sin2α = 0, имеем tg2α = |
1. |
||||||||
|
|
|
α |
x′ |
|
Следовательно, α1,2 = ±45°. |
|
|
|
|
|||||
|
|
|
01 |
|
|
|
Возьмем α = 45°, cos45° = sin45° = |
2 2. |
|
||||||
|
|
|
|
|
После соответствующих вычислений получаем |
||||||||||
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
3 |
2 |
|
1 |
2 |
93 |
|
|
|
|
|
|
|
|
|
|
2 x′′ |
|
+ |
2 y′′ |
|
= 25. |
|
|
|
|
|
′′2 |
|
|
|
y |
′′2 |
|
|
Итак, |
x |
+ |
|
|
|
=1 |
||
62 25 |
186 25 |
|||||||
|
|
|
||||||
– уравнение эллипса |
|
|||||||
с полуосями a = |
62 5 ≈1,5; |
|||||||
|
b = |
186 5 ≈ 2,7 |
||||||
в дважды штрихованной системе координат, получаемой из исходной параллельным переносом осей координат в точку О1(7/3, -8/3) и последующим поворотом на угол 45° против часовой стрелки.
Уравнение x2 + y2 + xy – 2x + 3y = 0 приведено к каноническому виду |
|||||
|
′′2 |
|
y |
′′2 |
|
|
x |
+ |
|
=1. |
|
|
a2 |
b2 |
|||
|
|
|
|||
Задача 18. Привести к каноническому виду уравнение
4x2 – 4xy + y2 – 2x – 14y + 7 = 0.
Решение
Система уравнений для нахождения центра кривой (формула (6) п.4.4)
|
4x |
− 2y |
|
−1 = 0, |
несовместна, |
|
0 |
|
0 |
|
|
|
−2x0 + y0 −7 = 0 |
|
|||
значит, данная кривая центра не имеет. Не меняя начала координат, повернем оси на некоторый угол α, соответствующие преобразования координат имеют
x = x′cosα − y′sin α,
вид:
y = x′sin α+ y′cosα.
44
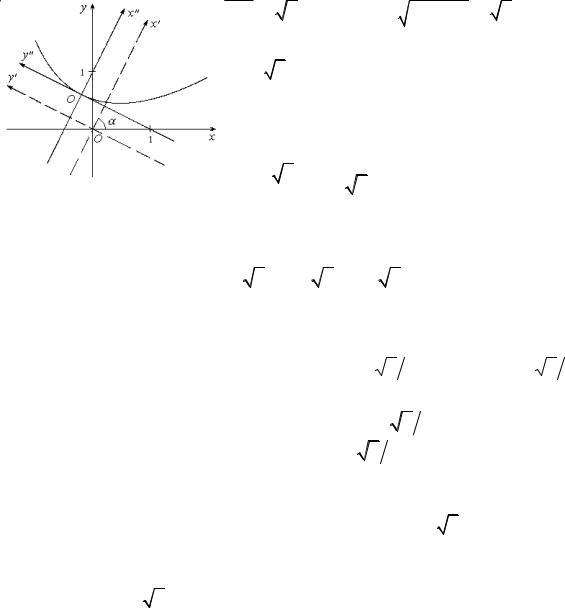
Перейдем в левой части уравнения к новым координатам: 4x2 – 4xy + y2 – 2x – 14y + 7 = (4cos2α - 4cosα sinα + sin2α) x′2 +
+2 (-4sinα cosα - 2cos2α + 2sin2α + sinα cosα) x′y′+
+(4sin2α + 4sinα cosα + cos2α) y′2 +
+2 (-cosα - 7sinα) x′+ 2 (sinα - 7cosα) y′+ 7. (*)
Постараемся теперь подобрать угол α так, чтобы коэффициент при х′у′ обратился в нуль. Для этого нам придется решить тригонометрическое уравнение -4sinα cosα - 2cos2α + 2sin2α + sinα cosα = 0.
Имеем 2sin2α - 3sinα cosα - 2cos2α = 0, или 2tg2α - 3tgα - 2 = 0.
Отсюда tgα = 2, или tgα = -1/2. Возьмем первое решение, что соответствует повороту осей на острый угол. Зная tgα, вычислим cosα и sinα:
cosα = |
|
1 |
= |
1 |
, |
sin α = |
|
tgα |
= |
2 |
. |
|
+tg2α |
5 |
|
+tg2α |
5 |
||||||
1 |
|
|
1 |
|
|
||||||
Отсюда, и учитывая (*), находим уравнение данной кривой в системе х′,у′:
5y |
′2 |
′ |
− 2 |
5y |
′ |
+ 7 |
= 0. |
(**) |
|
−6 5x |
|
Дальнейшее упрощение уравнения (**) производится при помощи параллельного перенесения осей Ох′, Оу′.
Перепишем уравнение (**) следующим образом:
5( y |
′2 |
− 2 |
5 |
′ |
′ |
+ 7 = 0. |
|
5 |
|||||||
|
y ) −6 5x |
||||||
Дополнив выражение в первой скобке до полного квадрата разности и компенсируя это дополнение надлежащим слагаемым, получим:
|
′ |
|
5 |
2 |
6 5 |
|
′ |
|
5 |
|
|
|
y |
− |
|
|
− |
|
|
− |
|
|
= 0. |
||
|
5 |
5 |
x |
5 |
||||||||
|
|
|
|
|
|
|
|
|
|
|||
Введем теперь еще новые координаты х′′,у′′, полагая |
|
|
|
||||||
|
|
x′= x′′+ 5 5, |
|
y′= y′′+ 5 5, |
|||||
|
|
что соответствует |
параллельному перемещению |
||||||
|
|
осей на величину |
|
5 5 в направлении оси Ох′ и |
|||||
|
|
на величину 5 5 |
|
|
в |
направлении оси Оу′. В |
|||
|
|
координатах х′′у′′ уравнение данной линии |
|||||||
|
|
принимает вид |
|
|
|
|
|
|
|
|
|
y |
′′ |
= |
6 5 |
′′2 |
. |
||
|
|
5 |
|||||||
|
|
|
x |
||||||
|
|
Это есть каноническое уравнение параболы с |
|||||||
параметром p = |
3 5 |
и с вершиной в начале координат системы х′′у′′. Парабола |
|||||||
5 |
|||||||||
|
|
|
|
|
|
|
|
||
расположена симметрично относительно оси х′′ и бесконечно простирается в
45
положительном направлении этой оси. Координаты вершины в системе х′у′
|
5 |
|
5 |
|
|
|
1 |
|
3 |
|
|
|
|
; |
|
|
а в системе ху |
− |
|
; |
|
. |
|
5 |
5 |
5 |
5 |
||||||||
|
|
|
|
|
|
|
Задача 19. Какую линию определяет уравнение 4x2 - 4xy + y2 + 4x - 2y - 3 =0?
Решение
Система для нахождения центра кривой в данном случае имеет вид:
|
|
|
|
4x − 2y |
+ 2 = 0, |
y |
|
2x-y+3=0 |
|
0 |
0 |
|
|||||
|
|
2x-y+1=0 |
|
−2x0 + y0 −1 = 0. |
|
|
|
|
|
|
|
|
|
2x-y-1=0 |
Эта система равносильна одному уравнению 2х0 – у0 |
||
|
|
+ 1 = 0, следовательно, линия имеет бесконечно |
|||
|
|
|
|||
|
|
|
много центров, составляющих прямую 2х – у + 1= 0. |
||
|
|
x |
Заметим, что левая часть данного уравнения |
||
|
|
|
разлагается на множители первой степени: |
||
|
0 |
|
|||
|
|
|
4х2 – 4ху + у2 + 4х –2у –3 = |
||
|
|
|
= (2х – у +3)(2х – у – 1). |
||
|
|
|
|||
Значит, рассматриваемая линия есть пара параллельных прямых: 2ху – у +3 = 0 и 2х – у – 1 = 0.
Задача 20 |
|
|
|
|
|
1. Уравнение 5х2 + 6ху + 5у2 – 4х + 4у + 12 = 0 |
′2 |
|
y |
′2 |
|
|
|
|
|||
приводится к каноническому виду х′2 + 4у′2 + 4 = 0, или |
x |
+ |
|
= −1. |
|
4 |
|
|
|||
|
1 |
|
|||
Это уравнение похоже на каноническое уравнение эллипса. Однако оно не определяет на плоскости никакого действительного образа, так как для любых действительных чисел х′,у′ левая часть его не отрицательна, а cправа стоит –1. Такое уравнение и аналогичные ему называются уравнениями мнимого эллипса.
2. Уравнение 5х2 + 6ху + 5у2 – 4х + 4у + 4 = 0 |
′2 |
|
y |
′2 |
|
|
|
|
|||
приводится к каноническому виду х′2 + 4у′2 = 0, или |
x |
+ |
|
= 0. |
|
4 |
|
|
|||
|
1 |
|
|||
Уравнение также похоже на каноническое уравнение эллипса, но определяет не эллипс, а единственную точку: х′ = 0, у′ = 0. Такое уравнение и аналогичные ему называются уравнениями вырожденного эллипса.
Задача 21. Составить уравнение параболы, если ее фокус находится в точке F(2, -1) и уравнение директрисы D: x – y – 1 = 0.
Решение
Пусть в некоторой системе координат х′О1у′ парабола имеет канонический вид у′2 = 2рх′. Если прямая у = х – 1 является ее директрисой, то оси системы координат х′О1у′ параллельны директрисе.
46

Координаты вершины параболы, совпадающей с новым началом координат О1, найдем как середину отрезка нормали к директрисе D, проходящей через фокус.
Итак, ось О1х′описывается уравнением
у = -х + b, -1 = -2 + b. Откуда b = 1 и О1х′: у = -х + 1.
Координаты точки K пересечения директрисы и оси О1х′ находим из условия:
y = |
x −1 |
, |
→ xК =1, yK = 0. |
|
|
||
y = −x +1 |
|
||
Координаты |
нового начала координат О1(х0, у0): |
|
||||
x =1+ 2 |
= 3 |
; y = −1+ 0 |
= −1 . Оси новой системы |
координат повернуты |
||
0 |
2 |
2 |
0 |
2 |
2 |
|
|
|
2. |
||||
относительно старой на угол (-45°). Найдем р = KF = |
||||||
Итак, уравнение параболы в старой системе координат получим, если
подвергнем уравнение параболы y′2 = 2 |
|
x′ преобразованию (см. формулу (5) |
|||||||||||||||||||
2 |
|||||||||||||||||||||
п.4.3): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
3 |
|
|
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|||
x′ = |
x − |
2 |
cos(−45°) + y + |
2 |
sin(−45°), |
|
|
x′ |
= |
|
(x − y − 2), |
||||||||||
|
|
2 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
→ |
|
|
|
|
||||||
|
|
|
|
|
3 |
|
|
|
|
1 |
|
|
|
|
|
|
2 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
y′ = − x − |
|
sin(−45°) + y + |
|
|
cos(−45°) |
y′ |
= |
|
(x + y −1), |
||||||||||||
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
y |
′2 |
|
|
|
′ |
|
1 |
(x + y |
−1) |
2 |
= 2 2 |
2 |
(x − y − 2), |
|
|
|
|
|
|||
|
|
|
2 |
|
2 |
|
|
|
|
|
|||||||||||
|
= 2 2 x |
|
|
|
|
|
|
||||||||||||||
откуда искомое уравнение параболы имеет вид: х2 + 2ху + у2 – 6х + 2у + 9 = 0. Задача 22. Написать уравнение гиперболы, если известны ее эксцентриситет
е = 5, фокус F(2, -3) и уравнение директрисы |
y′ |
|
y |
|
|||
|
|
|
|
|
|
|
|
3х – у + 3 = 0. |
|
|
|
|
|
D1 |
|
|
|
|
|
|
|
|
|
Решение |
|
|
|
|
|
3 B |
|
Уравнение директрисы D1: у = 3х + 3 позволяет |
|
|
|
||||
|
|
|
|
||||
заключить, что новая ось координат Ох′ имеет |
|
|
|
|
|||
вид y = (-1/3)x + b, проходит через точку F(2, - |
-7 |
-1 |
α |
x |
|||
1 |
+b, |
откуда b = -7/3 и Ох′ |
O1 |
A |
0 |
|
|
|
|
|
|||||
3), значит, −3 = −3 2 |
|
|
K |
|
|||
|
|
|
|
|
|
|
|
|
|
1 x − |
7 . |
a / |
5 |
-7/3 |
x′ |
задается уравнением |
y = − |
|
|
F |
|||
|
|
3 |
3 |
|
|
|
|
Пусть начало новой системы координат находится в точке О1(х0, у0). Найдем координаты точки К как координаты точки пересечения директрисы D1 и
47
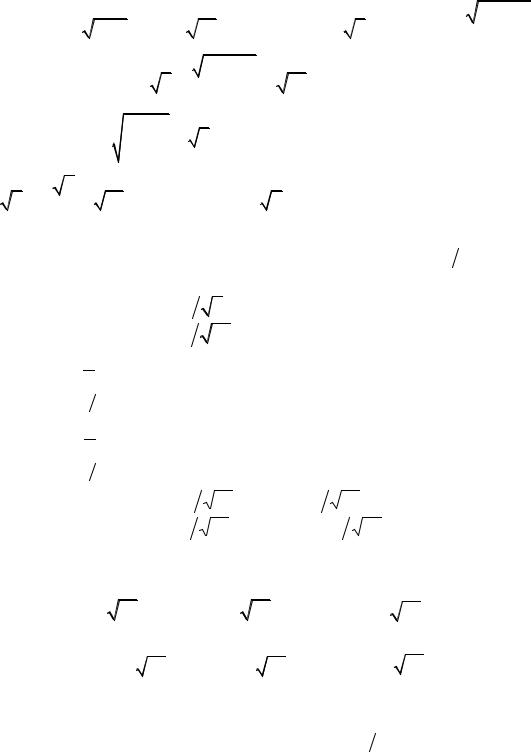
3x − y +3 = 0, |
→ xK |
= − |
8 |
, yK |
= − |
9 . |
||
оси Ох′′ из системы |
3y + x + 7 |
= 0 |
||||||
|
|
|
5 |
|
|
5 |
||
|
|
|
Геометрические свойства |
|
|
гиперболы, |
которая |
в |
новых |
|
осях |
координат |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Ох′у′имеет вид |
|
|
|
x |
′2 |
|
|
|
y |
′2 |
=1, |
позволяют найти КF как расстояние от фокуса |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
− |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
a2 |
|
|
b2 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
F(2, -3) до директрисы D1: 3х – у + 3 = 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
KF = |
|
3 (2) −(−3) +3 |
|
= |
12 |
|
, |
|
|
|
|
|
|
|
O K |
= a = |
|
a |
, |
|
O F |
= c = |
a2 +b2 , |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
9 +1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
e |
|
|
5 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
O K =O F |
− KF |
|
a |
|
= a2 +b2 − |
12 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
так |
как |
|
e = |
1+ |
|
b2 |
= |
|
|
5, |
|
|
|
b |
2 |
= 4a |
2 |
. Значение |
а |
|
находим |
|
из |
уравнения |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
a2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
a |
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
= a |
5 − |
|
|
|
|
|
|
и получаем a = |
|
|
. При этом b2 = 18. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
5 |
|
|
|
10 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′2 |
|
y |
′2 |
|
|
|
|
Уравнение гиперболы в новых координатах имеет вид |
x |
− |
|
|
=1. |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
9 2 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
18 |
|
|
|
|
|||||
Координаты нового центра найдем, зная что точка К делит отрезок О1F в |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
отношении λ = |
O1K |
= |
|
|
a |
|
5 |
|
= |
1 |
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
10 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
KF |
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
x0 |
+ |
1 |
xF |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
xK |
= |
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x0 = − |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
1 |
+ |
1 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
y0 + |
yF |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y0 = − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
yK |
= |
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
1 |
+1 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
Из ∆ АВО: sinα = 1 |
10 , |
|
|
cosα = 3 |
10 . Так как поворот совершается на |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
угол (-α): sin(-α) = −1 |
|
10 , cos(-α) = 3 |
10 , |
|
то формулы преобразований |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
координат (см. (5) в п.4.3) принимают вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
5 3 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
(3x − y + 6), |
|
|
|||||||||||||||||||||||||||||||
x′ = x |
+ |
2 |
|
|
|
|
|
|
|
|
+ |
y |
+ |
|
2 |
|
− |
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
x′ |
= |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
→ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
3 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x +3y + 7) |
|
|
||||||||||||||||||||||||||||||||||||||
y′ |
= − |
x + |
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
+ |
|
y |
+ |
2 |
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
y′ = |
10 |
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
(3x − y + 6)2 |
|
1 |
(x +3y + 7)2 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
10 |
|||||||||||||||||||
и уравнение гиперболы принимает вид |
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
=1, |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
9 2 |
|
|
|
|
|
|
|
18 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
4(3х – у +6)2 – (х + 3у + 7)2 = 180 |
или 7х2 – у2 – 6ху – 18у + 26х + 17 = 0. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
48
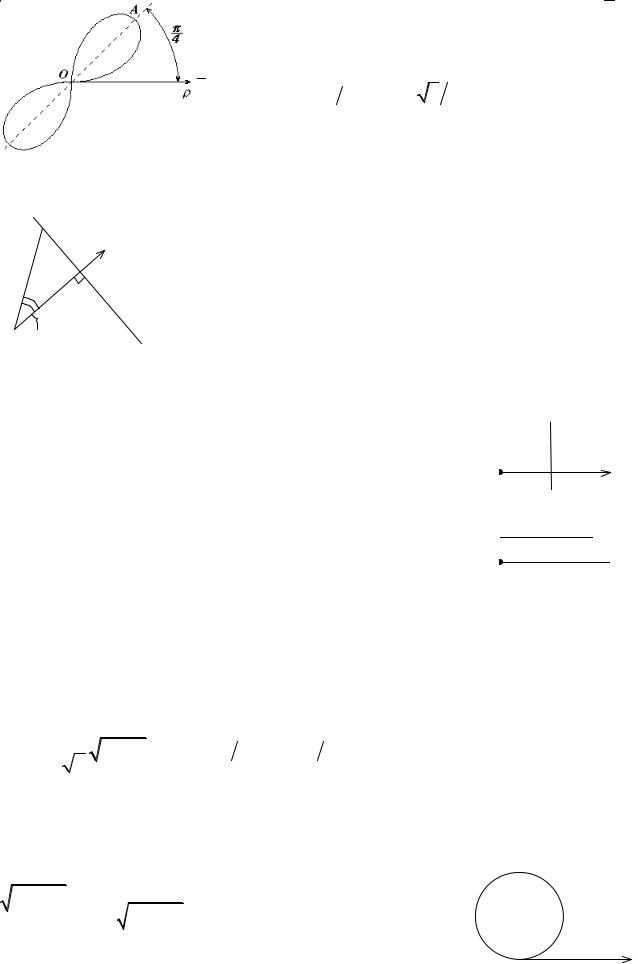
Задача 23. Найти полярный угол отрезка, направленного из точки (5, 
 3 ) в
3 ) в
точку (6, 2
 3 ).
3 ).
Решение
ρ= (6 −5)2 + (2 3 − 3)2 = 2, |
cosϕ =1 2, sin ϕ = 3 2 ϕ= 60°. |
(см. п.5.2).
Задача 24. Составить уравнение прямой в полярных координатах, считая известными расстояние р от полюса до прямой и угол α от полярной оси до луча, направленного из полюса перпендикулярно к прямой.
M (ρ, ϕ)
L
βP
Решение
Известны ОР = р, РОА = α, произвольная точка М прямой L имеет координаты (ρ, ϕ).
Точка М лежит на прямой L в том и только в том случае,
αкогда проекция точки М на луч ОР совпадает с точкой Р,
|
|
|
т.е. когда р = ρ cosβ, где РОМ = β. Угол ϕ = α + β и |
O |
A |
||
|
|
|
уравнение прямой L принимает вид ρ cos(ϕ - α) = p. |
Задача 25. Найти полярные уравнения указанных кривых: 1). x = a, a > 0
Решение
ρ cosϕ = a → ρ = a/cosϕ.
|
a |
0 |
ρ |
2). y = b, b > 0
Решение
ρ sinϕ = b |
→ ρ = b/sinϕ. |
|
0 |
||||||
3). (х2 + у2)2 = а2ху |
|
|
|||||||
Решение: xy ≥ 0, |
|
|
|||||||
ρ4 = a2ρ2 cosϕsin ϕ→ ρ2 = a2 |
sin 2ϕ, |
sin 2ϕ≥ 0. |
|||||||
|
|
|
|
|
|
2 |
|
|
|
Уравнение кривой в полярных координатах имеет |
|||||||||
вид ρ = |
|
|
a |
|
|
|
sin 2ϕ, ϕ [0, π 2] [π, 3π 2] и задает |
||
|
|
|
|||||||
|
|
||||||||
|
|
|
|
|
|
||||
2 |
|
|
|
|
|||||
двухлепестковую розу:
Задача 26. Построить заданные в полярной системе координат линии: 1). ρ = 2a sinϕ, a > 0.
Решение |
y |
|
|
|
|
|
|
|
|
|
|
|
|||
x2 + y2 = 2a |
|
, |
|
|
|
|
|
x2 |
+ y2 |
|
|
|
|
||
|
|
|
|
|
a |
||
x2 + y2 – 2ay = 0, |
|
0 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
b
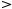 ρ
ρ
ρ
49
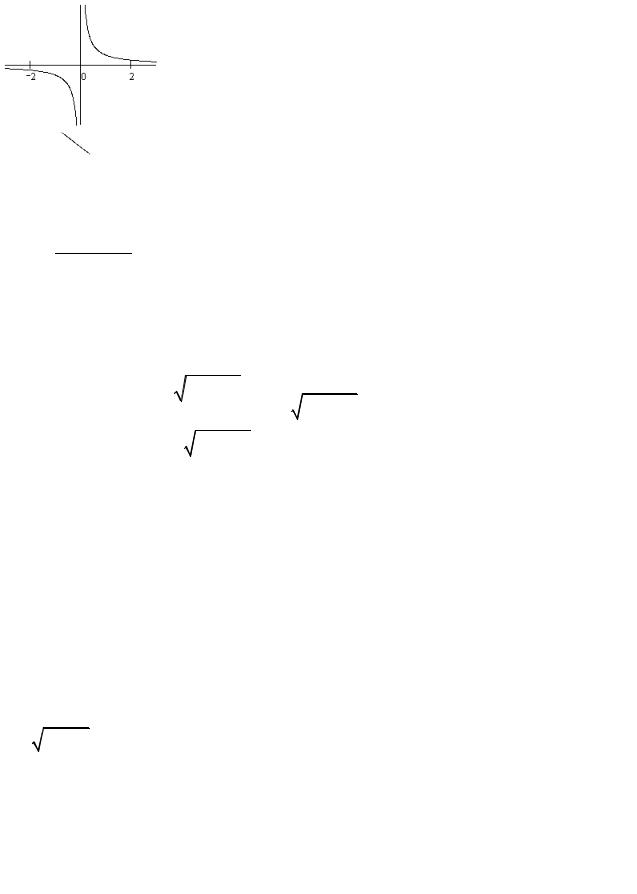
x2 + (y – a)2 = a2. 2). ρ = 2 + cosϕ.
Решение
Линия получается, если каждый радиус-вектор окружности
ρ = cosϕ увеличить на два. Найдем координаты контрольных точек:
ϕ= 0, ρ = 3;
ϕ= π/2, ρ = 2;
ϕ= π, ρ = 1.
3). ρ = 9
4 −5cosϕ
Решение
4 – 5 cosϕ > 0, cosϕ < 4/5, ϕ (arccos(4/5), 2π – arccos(4/5)).
При этом ρ (4 - 5 cosϕ) = 9. Переходя к декартовым координатам, получаем
x |
2 |
+ y |
2 |
|
|
|
|
x |
|
|
|
|
|
4 |
−5 |
|
|
|
|
|
= 9, |
||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
x |
2 |
+ y |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||
4 x2 + y2 = 5x +9, 16(x2 + y2 )= (5x +9)2 ,
16x2 + 16y2 = 25x2 + 90x + 81, 9x2 + 90x – 16y2 +81 = 0,
|
2 |
2 |
|
(x +5)2 |
|
y |
2 |
|
|
9(x + 5) |
|
– 16y = 144 |
→ |
|
2 |
− |
|
|
=1 |
|
4 |
3 |
2 |
||||||
|
|
|
|
|
|
|
|
||
гиперболы при указанных ϕ.
Кривую можно было построить по точкам, например, при ϕ = π 4). ρ2 sin2ϕ = а2.
–правая ветвь
ρ= 9/10.
Решение
sin 2ϕ≥ 0, ϕ [0, π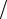 2] [π, 3π
2] [π, 3π 2].
2].
ρ = |
|
a |
|
. |
|
|
|
|
|||
sin 2ϕ |
|||||
|
|
||||
Перейдем к декартовым координатам, учтем, что
sin 2ϕ = 2cos ϕ sin ϕ |
ρ2 |
= |
2xy |
, |
|
ρ2 |
x2 + y2 |
||||
|
|
|
тогда кривая принимает вид гиперболы: y = a2 2 . x
2 . x
Задача 27. Какие линии задаются следующими параметрическими уравнениями:
50

|
|
x = 3cost, |
t [0, 2π]. |
||||||
1). |
|
|
|
|
|
||||
|
|
y = 2sin t, |
|
||||||
Решение |
|
|
|||||||
|
x2 |
y2 |
|
|
|
||||
|
|
+ |
|
|
=1 - эллипс. |
||||
2 |
2 |
2 |
|||||||
3 |
|
|
|
|
|
|
|||
|
|
|
|
|
2 |
|
|
||
2). x = t |
− 2t |
+1, t R. |
|||||||
|
|||||||||
|
|
y = t −1, |
|
||||||
Решение
у2 = x – парабола.
x = −1 + 2 cost, |
t [0, 2π]. |
|
3). |
y = 3 + 2sin t, |
|
|
|
|
Решение
(x + 1)2 + (y – 3)2 = 4 –окружность;
x = 2t −1, |
|
t R. |
|
4). |
− 4t2 |
, |
|
y =1 |
|
||
Решение
y = -x2 – 2x, y – 1 = -(x + 1)2 – парабола с вершиной в точке (-1, 1).
|
3 |
|
|
|
Задача 28. Выведите уравнение астроиды x = acos |
t, |
t [0, 2π], |
||
|
||||
y = asin3 t, |
|
|||
в полярной системе координат.
Решение
x2 + y2 = a2(sin6t + cos6t) = a2(sin2t + cos2t) (sin4t + cos4t – sin2t cos2t) =
=a2(sin4t + cos4t + 2sin2t cos2t – 3sin2t cos2t) = a2((sin2t + cos2t)2 – 3sin2t cos2t) =
=a2(1 – 3sin2t cos2t) = a2(1 – (3/4) sin22t).
51
