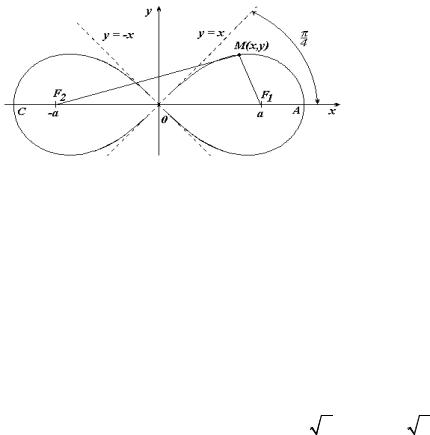
8.3. Лемниската Бернулли
Лемниската Бернулли - линия, представляющая геометрическое место точек, расстояние которых от двух данных точек (фокусов) есть постоянная величина, равная квадрату половины межфокусного расстояния.
Уравнение лемнискаты Бернулли в декартовых координатах
(x2 + y2 )2 −2a2 (x2 − y2 ) = 0 ,
в полярных координатах
ρ2 = 2a2 cos2ϕ, a > 0.
Укажем, что точка М лежит на кривой, если выполнено условие
|
|
|
|
|
|
F F |
|
|
2 |
|
|
|
|
||||||||
|
F1M |
|
F2M |
= |
|
|
1 2 |
|
|
. |
|
|
|
||||||||
|
|
2 |
|
|
||||||
|
|
|
|
|
|
|
|
|||
Вершины кривой находятся в точках A(a |
|
2,0); C(−a 2,0). |
||||||||
Площадь каждой петли S=a2.
27
ФОРМУЛЫ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ НА ПЛОСКОСТИ
d = (x − x )2 |
+ ( y |
2 |
− y )2 |
|||
|
|
2 |
1 |
|
1 |
|
x |
= x1 + λ x2 |
, |
|
|
||
|
|
1+ λ |
|
|
|
|
|
|
y1 + λ y2 |
|
|
|
|
|
|
, |
|
|
||
y |
= |
1 |
+ λ |
|
|
|
|
|
|
|
|
||
λ ≠ −1 |
|
|
|
|
||
-расстояние между точками A(x1,y1) и B(x2,y2);
-координаты точки С(x,y), которая делит отрезок, соединяющий точки A(x1,y1) и
B(x2,y2), в отношении λ = CBAC ;
x = x1 +2 x2 ; y = y1 +2 y2
|
x1 |
|
y1 |
1 |
|
|
|
|
|
|
|
|||
|
x2 |
|
y2 |
1 |
= 0 |
|
|
|
|
|||||
|
x3 |
|
y3 |
1 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
x1 |
|
y1 |
|
1 |
|
|
|
||
S = |
|
x |
|
y |
|
|
1 |
= |
|
|
||||
|
|
|
2 |
|
2 |
|
|
2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
x |
|
y |
|
|
|
|
||
|
|
|
|
|
|
3 |
|
|
3 |
|
|
|
|
|
= |
1 |
|
x2 − x1 |
|
y2 − y1 |
|
|
|||||||
|
|
|
||||||||||||
2 |
|
x |
− x |
|
y |
− y |
|
|
||||||
|
|
|
|
|
|
|||||||||
|
|
|
|
3 |
|
1 |
|
|
3 |
1 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ax+By+C=0
A(x-x0)+B(y-y0)=0
x −l x0 = y −my0
x = x0 +lt,y = y0 + mt, t ( −∞,∞)
-координаты середины отрезка АВ;
-условие принадлежности трёх точек (x1,y1), (x2,y2), (x3,y3) одной прямой;
-модуль этих выражений даёт площадь треугольника с вершинами (x1,y1), (x2,y2),
(x3,y3).
Прямая на плоскости
-общее уравнение прямой;
-уравнение прямой, проходящей через точку
(x0,y0) перпендикулярно нормальному вектору
{A,B};
-каноническое уравнение прямой,
проходящей через точку (x0,y0) параллельно вектору {l,m};
-параметрические уравнения прямой, проходящей через точку (x0,y0) параллельно
вектору {l,m};
28
|
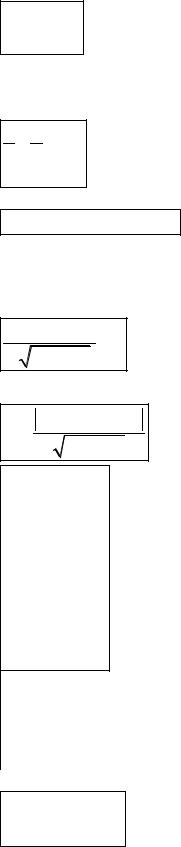
y − y1 |
= |
x − x1 |
|
|||
|
y |
2 |
− y |
|
x |
− x |
|
|
|
1 |
|
2 |
1 |
|
|
y = kx +b, k = tgα
ax + by =1, a ≠ 0, b ≠ 0
xcosα + y sinα − p = 0
Ax + By +C = 0
± A2 + B2
d = Ax0 + By0 +C |
A2 + B2 |
|
|
|
|
|
|
B1 |
C1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
B2 |
C2 |
|
|
|
|
|
|
|
|
x |
|
= |
|
|
|
|
|
|
|
|
, |
||||
|
|
|
|||||||||||||
|
|
|
|
A1 |
B1 |
|
|
|
|
|
|
||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
A2 |
B2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
C1 |
A1 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
C2 |
A2 |
|
|
|
|
||||
y |
|
= |
|
|
|
|
|
|
|||||||
|
|
|
|
||||||||||||
0 |
|
|
|
A1 |
B1 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
A2 |
B2 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
b |
−b |
|
|
x0 |
= |
2 |
1 |
, |
|
||
k1 |
|
|
|||||
|
|
|
− k2 |
|
|||
|
|
|
|
b2 k1 −b1k2 |
|
||
y |
|
= |
|
||||
|
|
|
|||||
|
0 |
|
|
|
k1 − k2 |
|
|
|
|
|
|
|
|
||
A1 B2 − A2 B1 = 0, k1 = k2
-уравнение прямой, проходящей через две заданные точки (x1,y1) и (x2,y2);
-уравнение прямой с угловым
|
π |
π |
|
- |
||
коэффициентом k, где α 0, |
2 |
|
|
2 |
,π |
|
|
|
|
|
|
||
угол наклона прямой к оси ox;
-уравнение прямой в отрезках, где (а,0) и (0,b) - координаты точек пересечения прямой с осями ox и oy;
-нормальное уравнение прямой, где р - расстояние от начала координат до прямой,
α-угол между осью ox и перпендикуляром к прямой, проходящей через начало координат;
-нормальный вид общего уравнения прямой; знак нормирующего множителя противоположен знаку С;
-расстояние от точки (x0,y0) до прямой
Ax+By+C=0;
-координаты точек пересечения двух прямых
A1x+B1y+C1=0 и A2x+B2y+C2=0;
-координаты точек пересечения прямых y=k1x+b1 и y=k2x+b2;
-условия параллельности прямых, заданных
в общем виде A1x+B1y+C1=0, A2x+B2y+C2=0
и в виде y=k1x+b1, y=k2x+b2 ;
29
A1 A2 |
+ B1 B2 |
= 0, |
|
- условие перпендикулярности прямых, |
||||
k1k2 = −1 |
|
|
|
|
заданных в общем виде |
|||
|
|
|
|
A1x+B1y+C1=0, A2x+B2y+C2=0 |
||||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
и в виде y=k1x+b1, y=k2x+b2 ; |
|
|
|
|
|
|
- угол α между двумя прямыми, заданными в |
|||
tgα = |
|
A1 B2 |
− A2 B1 |
, |
||||
|
|
|
|
общем виде |
A1x+B1y+C1=0, |
|||
|
A1 A2 |
+ B1 B2 |
||||||
|
|
k1 − k2 |
|
|
|
A2x+B2y+C2=0 |
|
|
|
|
|
|
|
|
|||
tgα = |
|
|
, |
|
и в виде y=k1x+b1, y=k2x+b2 ; |
|||
|
1+ k1k2 |
|
|
|||||
|
|
|
|
|
|
|
||
k1k2 ≠ −1, |
|
|
|
|
|
|
||
α = π |
|
, если k1k2 = −1. |
|
|
||||
2 |
|
|
|
|
|
|
|
|
30
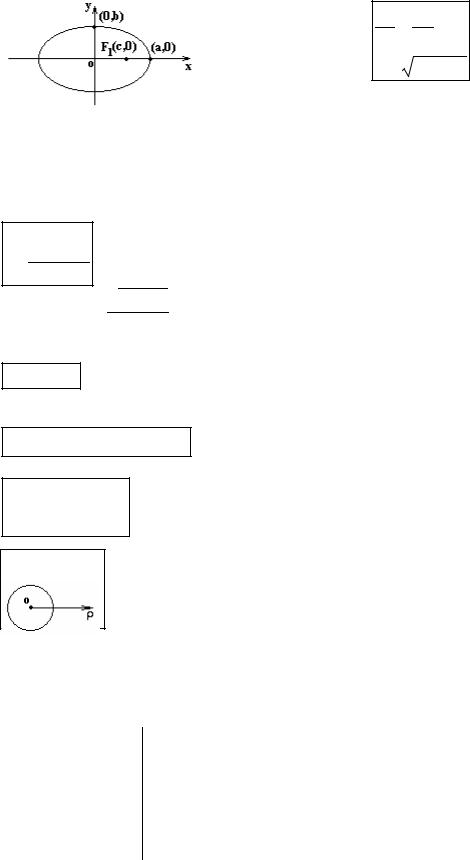
Кривые второго порядка Эллипс
x2 |
+ y2 |
=1, |
- |
a2 |
b2 |
|
|
c = |
a2 |
−b2 |
|
- каноническое уравнение эллипса, если координатные оси совпадают с осями эллипса;
x = a cost, |
- параметрические уравнения эллипса, где t-параметр, t [0,2π) ; |
|
|
y = bsin t |
|
(t - угол, образованный подвижным радиусом с положительным направлением оси ox);
b2
ρ = a - уравнение эллипса в полярных координатах, связанных с
1−ecosϕ
фокусом, e = 
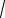a2 −b2 - эксцентриситет эллипса. a
x2 + y2 =R2
(x − x0 )2 + ( y − y0 )2 = R2
x = x0 + R cost,
y = y0 + Rsin t
ρ = R
Окружность
-уравнение окружности радиуса R с центром в начале координат;
-с центром в точке (x0,y0);
-параметрические уравнения окружности с радиусом R и центром в точке (x0,y0);
-уравнение окружности в полярных координатах;
|
ρ2 −2ρρ0 cos(ϕ−ϕ0 |
) +ρ02 = R2 |
- |
уравнение окружности с центром в точке |
|
|
|
|
|
(α 0,ϕ0); |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
31