
Решения по физике вариант 0
.docx304. Два положительных точечных заряда q и 4q закреплены на расстояния 60 см друг от друга. Определить, в какой точке на прямой, проходящей через заряды, следует поместить третий заряд так, чтобы он находился в равновесии. Указать, какой знак должен иметь этот заряд для того, чтобы равновесие было устойчивым, если перемещения заряда возможны только вдоль прямой, проходящей через закрепленные заряды.
Дано:

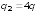
 см
см
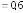 м
м
Найти:
 .
.
Решение.
Положение помещаемого заряда
 будем отмечать расстоянием
будем отмечать расстоянием
 от первого заряда
от первого заряда
 .
Тогда расстояние от
.
Тогда расстояние от
 до
до
 будет
будет
 .
По условию векторная сумма сил, действующих
на заряд
.
По условию векторная сумма сил, действующих
на заряд
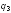 ,
должна равняться нулю. На него будут
действовать две силы
,
должна равняться нулю. На него будут
действовать две силы
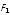 и
и
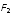 электростатического взаимодействия
со стороны двух остальных. Так как заряды
находятся на одной линии, то для взаимной
компенсации эти силы должны быть
направлены в противоположные стороны.
электростатического взаимодействия
со стороны двух остальных. Так как заряды
находятся на одной линии, то для взаимной
компенсации эти силы должны быть
направлены в противоположные стороны.
Рассмотрим
равновесие заряда
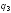 .
На него со стороны двух положительных
зарядов
.
На него со стороны двух положительных
зарядов
 и
и
 будут действовать силы по закону Кулона:
будут действовать силы по закону Кулона:
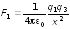 ,
,
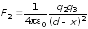 ,
,
где
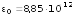 Ф/м — электрическая постоянная. Тогда
по условию равновесия
Ф/м — электрическая постоянная. Тогда
по условию равновесия
 ,
,
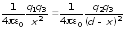 ,
,
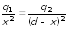 ,
,
или, с учетом значений для зарядов,
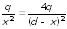 или
или
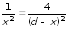 .
.
Отсюда
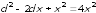 ,
,
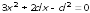 .
.
Решим
полученное квадратное уравнение
относительно
 :
:
 ,
,
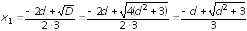 ,
,
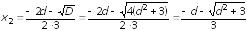 .
.
Второе
решение дает отрицательное значение
для
 ,
поэтому его отбрасываем, т.к. в этом
случае заряд
,
поэтому его отбрасываем, т.к. в этом
случае заряд
 будет находиться левее заряда
будет находиться левее заряда
 .
При этом, хотя силы
.
При этом, хотя силы
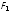 и
и
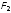 и будут равны, но направлены в одну
сторону и не скомпенсируют друг друга.
Таким образом,
и будут равны, но направлены в одну
сторону и не скомпенсируют друг друга.
Таким образом,
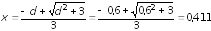 м.
м.
Для
того, чтобы заряд
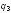 был в устойчивом равновесии, необходимо,
чтобы он был положительным. Только в
этом случае при его сдвиге в любую
сторону появляется сила, стремящаяся
вернуть его на прежнее место. Например,
если сдвинуть
был в устойчивом равновесии, необходимо,
чтобы он был положительным. Только в
этом случае при его сдвиге в любую
сторону появляется сила, стремящаяся
вернуть его на прежнее место. Например,
если сдвинуть
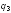 влево, то, как видно из закона Кулона,
сила
влево, то, как видно из закона Кулона,
сила
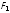 увеличится, а сила
увеличится, а сила
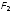 — уменьшится. И наоборот, если сдвинуть
— уменьшится. И наоборот, если сдвинуть
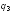 вправо, то сила
вправо, то сила
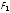 уменьшится, а сила
уменьшится, а сила
 — увеличится. Если бы заряд
— увеличится. Если бы заряд
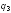 был отрицательным, то направления сил
был отрицательным, то направления сил
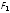 и
и
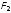 были бы противоположными показанным
на рисунке. В этом случае сдвиг заряда
были бы противоположными показанным
на рисунке. В этом случае сдвиг заряда
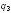 привел бы к еще большему увеличению
результирующей силы, стремящейся
сдвинуть заряд в сторону.
привел бы к еще большему увеличению
результирующей силы, стремящейся
сдвинуть заряд в сторону.
Ответ:
 м; заряд должен быть положительным.
м; заряд должен быть положительным.
312. На тонком кольце равномерно
распределен заряд с линейной плотностью
заряда
 = 20 нКл/см. Радиус кольца r
= 5 см.
На перпендикуляре к плоскости кольца,
восстановленном из его середины,
находится точечный заряд q
= 40 нКл. Определить силу, действующую на
точечный заряд со стороны заряженного
кольца, если он удален от центра кольца
на: 1) а1
= 10 см; 2) а2
= 2 м.
= 20 нКл/см. Радиус кольца r
= 5 см.
На перпендикуляре к плоскости кольца,
восстановленном из его середины,
находится точечный заряд q
= 40 нКл. Определить силу, действующую на
точечный заряд со стороны заряженного
кольца, если он удален от центра кольца
на: 1) а1
= 10 см; 2) а2
= 2 м.
Дано:
 нКл/см
нКл/см
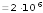 Кл/м
Кл/м
 см
см
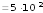 м
м
 нКл
нКл
 Кл
Кл
 см
см
 м
м
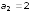 м
м
Найти:
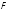 .
.
Решение.
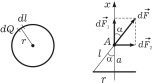
Разобьем
кольцо на бесконечно малые элементы
длины
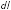 ,
каждый из которых несет бесконечно
малый заряд
,
каждый из которых несет бесконечно
малый заряд
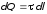 .
.
Этот
заряд действует на заряд
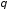 в точке на оси кольца на расстоянии
в точке на оси кольца на расстоянии
 от центра с силой, согласно закону Кулона
равной
от центра с силой, согласно закону Кулона
равной
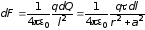 ,
,
где
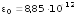 Ф/м — электрическая постоянная.
Результирующая сила со стороны всех
бесконечно малых зарядов равна векторной
сумме сил
Ф/м — электрическая постоянная.
Результирующая сила со стороны всех
бесконечно малых зарядов равна векторной
сумме сил
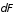 ,
создаваемых каждым из зарядов
,
создаваемых каждым из зарядов
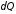 .
Суммирование бесконечно малых есть
интегрирование, поэтому
.
Суммирование бесконечно малых есть
интегрирование, поэтому
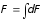 .
.
Из
рисунка видно, что вектор
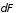 можно разложить на две взаимно
перпендикулярные составляющие
можно разложить на две взаимно
перпендикулярные составляющие
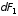 и
и
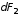 .
Составляющие
.
Составляющие
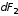 от двух попарно противоположных зарядов
от двух попарно противоположных зарядов
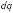 направлены противоположно, поэтому при
интегрировании дадут нуль. Составляющие
направлены противоположно, поэтому при
интегрировании дадут нуль. Составляющие
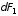 от всех зарядов
от всех зарядов
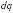 направлены в одну сторону. Тогда мы
можем заменить векторное суммирование
алгебраическим:
направлены в одну сторону. Тогда мы
можем заменить векторное суммирование
алгебраическим:
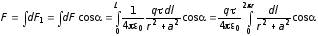 ,
,
где
интегрирование ведется по всей длине
кольца
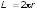 .
Из рисунка видно, что
.
Из рисунка видно, что
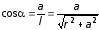 .
.
Тогда
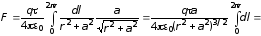
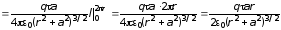 .
.
Подставляя
числовые данные, получим значения силы
для двух заданных расстояний
 :
:
1)
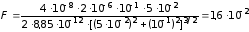 Н;
Н;
2)
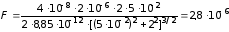 Н.
Н.
Ответ:
1)
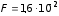 Н; 2)
Н; 2)
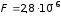 Н.
Н.
317. Параллельно бесконечной плоскости,
заряженной с поверхностной плотностью
заряда σ = 10–6
Кл/м2, расположена
бесконечно длинная прямая нить, заряженная
с линейной плотностью
 = 10–8 Кл/м. Определить
силу, действующую со стороны плоскости
на единицу длины нити.
= 10–8 Кл/м. Определить
силу, действующую со стороны плоскости
на единицу длины нити.
Дано:
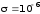 Кл/м2
Кл/м2
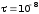 Кл/м
Кл/м
Найти:
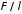 .
.
Решение.
Бесконечная плоскость, заряженная с
поверхностной плотностью
 ,
создает около себя однородное электрическое
поле с напряженностью
,
создает около себя однородное электрическое
поле с напряженностью
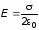 ,
,
где
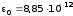 Ф/м — электрическая постоянная. В этом
поле находится распределенный по прямой
бесконечной нити заряд, соответственно,
на этот заряд со стороны электрического
поля действует сила.
Ф/м — электрическая постоянная. В этом
поле находится распределенный по прямой
бесконечной нити заряд, соответственно,
на этот заряд со стороны электрического
поля действует сила.
Разобьем
нить на бесконечно малые участки длины
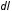 ,
заряд каждого из которых равен
,
заряд каждого из которых равен
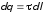 .
.
Бесконечно малая сила, действующая на этот заряд со стороны электрического поля, равна
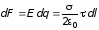 .
.
Направление
этой силы для каждого участка
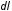 одинаково, поэтому результирующая сила,
действующая на участок нити длиной
одинаково, поэтому результирующая сила,
действующая на участок нити длиной
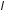 ,
равна алгебраической сумме бесконечно
малых сил:
,
равна алгебраической сумме бесконечно
малых сил:
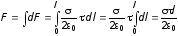 .
.
Тогда сила, приходящаяся на единицу длины нити, равна
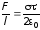 .
.
Вычисление:
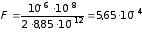 Н.
Н.
Ответ:
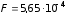 Н.
Н.
320. Электрическое поле образовано
бесконечно длинной нитью, заряженной
с линейной плотностью
 = 10–10 Кл/м.
Определить разность потенциалов U
двух точек поля, отстоящих от нити на
расстоянии r1
= 5 см и r2 = 10 см.
= 10–10 Кл/м.
Определить разность потенциалов U
двух точек поля, отстоящих от нити на
расстоянии r1
= 5 см и r2 = 10 см.
Дано:
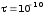 Кл/м
Кл/м
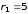 см
см
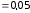 м
м
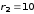 см
см
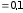 м
м
Найти:
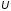 .
.
Решение.
Для решения задачи воспользуемся связью
между напряженностью
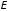 и потенциалом
и потенциалом
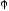 электрического поля:
электрического поля:
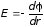 ,
,
откуда разность потенциалов
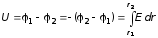 .
.
Напряженность,
создаваемая нитью на расстоянии
 ,
равна
,
равна
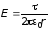 ,
,
где
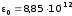 Ф/м — электрическая постоянная. Тогда
Ф/м — электрическая постоянная. Тогда
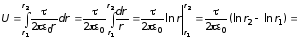
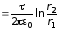 .
.
Вычисление:
 В.
В.
Ответ:
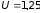 В.
В.
332. Пространство между пластинами плоского конденсатора заполнено двумя слоями диэлектриков: слоем стекла толщиной d1 =1 см и слоем парафина толщиной d2 = 2 см. Разность потенциалов между обкладками U = 3000 В. Определить напряженность поля и падение потенциала в каждом из слоев.
Дано:
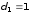 см
см
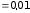 м
м
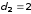 см
см
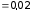 м
м
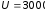 В
В
Найти:
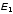 ,
,
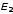 ,
,
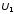 ,
,
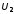 .
.
Решение. Разности потенциалов на слоях и напряженности электрического поля внутри слоев связаны соотношениями
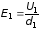 ,
,
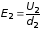 ,
,
где
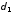 ,
,
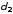 — толщины слоев. С другой стороны, если
бы не было диэлектриков, поле внутри
конденсатора имело бы значение
— толщины слоев. С другой стороны, если
бы не было диэлектриков, поле внутри
конденсатора имело бы значение
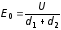 .
.
Но
это поле в диэлектриках ослабляется в
 раз, где
раз, где
 — диэлектрическая проницаемость
диэлектрика:
— диэлектрическая проницаемость
диэлектрика:
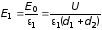 ,
,
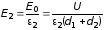 .
.
Для
стекла
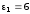 ,
для парафина
,
для парафина
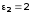 .
Тогда
.
Тогда
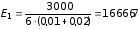 В/м;
В/м;
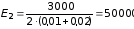 В/м.
В/м.
Падения потенциалов пропорциональны толщинам слоев:
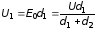 ,
,
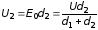 .
.
Вычисление:
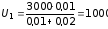 В,
В,
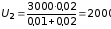 В.
В.
Ответ:
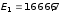 В/м;
В/м;
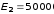 В/м;
В/м;
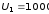 В;
В;
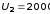 В.
В.
330. Электрон с энергией Т = 100 эВ (в бесконечности) движется вдоль силовой линии по направлению к поверхности металлической заряженной сферы радиусом R = 5 см. Определить минимальное расстояние, на которое приблизится электрон к поверхности сферы, если ее заряд q = –10–9 Кл.
Дано:
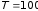 эВ
эВ
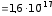 Дж
Дж
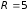 см
см
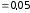 м
м
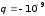 Кл
Кл
Найти:
 .
.
Решение.
Электрон — отрицательно заряженная
частица. По условию сфера тоже заряжена
отрицательно. Поэтому между сферой и
электроном будет наблюдаться отталкивание.
При приближении электрона к сфере его
кинетическая энергия будет уменьшаться.
На наименьшем расстоянии
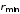 от центра сферы электрон останавливается
и его кинетическая энергия полностью
переходит в потенциальную энергию
взаимодействия со сферой:
от центра сферы электрон останавливается
и его кинетическая энергия полностью
переходит в потенциальную энергию
взаимодействия со сферой:
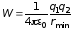 ,
,
где
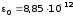 Ф/м — электрическая постоянная;
Ф/м — электрическая постоянная;
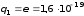 Кл — заряд (по модулю) электрона;
Кл — заряд (по модулю) электрона;
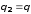 — заряд (по модулю) сферы.
— заряд (по модулю) сферы.
По закону сохранения и превращения энергии имеем
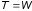 или
или
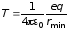 ,
,
откуда
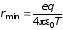 .
.
Тогда расстояние от электрона до поверхности сферы в этот момент равен
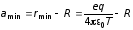 ,
,
где
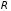 — радиус сферы.
— радиус сферы.
Вычисление:
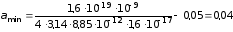 м.
м.
Ответ:
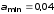 м.
м.
347. Ток в проводнике равномерно увеличивается от нуля до некоторого максимального значения в течение t =10 с. За это время в проводнике выделилась теплота Q = 103 Дж. Определить скорость нарастания тока в проводнике, если сопротивление его r = 3 Ом.
Дано:
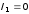
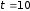 с
с
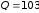 Дж
Дж
 Ом
Ом
Найти:
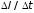 .
.
Решение.
Количество теплоты
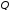 ,
выделяющейся в проводнике за время
,
выделяющейся в проводнике за время
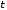 ,
вычисляется по закону Джоуля–Ленца
,
вычисляется по закону Джоуля–Ленца
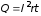 ,
,
где
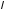 — сила тока через проводник;
— сила тока через проводник;
 — его сопротивление. Так как сила тока
возрастает, то необходимо рассматривать
бесконечно малый промежуток времени
— его сопротивление. Так как сила тока
возрастает, то необходимо рассматривать
бесконечно малый промежуток времени
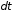 ,
в течение которого выделяется бесконечном
малое количество теплоты, при этом за
этот промежуток времени ток считаем
постоянным:
,
в течение которого выделяется бесконечном
малое количество теплоты, при этом за
этот промежуток времени ток считаем
постоянным:
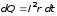 .
.
Общее количество теплоты находится суммированием, т.е. интегрированием бесконечно малых:
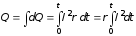 .
.
Зависимость
силы тока
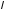 от времени
от времени
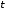 при ее равномерном (линейном) возрастании
во времени можно представить в виде
при ее равномерном (линейном) возрастании
во времени можно представить в виде
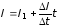 ,
,
где
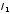 — начальный ток (при
— начальный ток (при
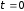 );
);
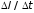 — искомая скорость возрастания силы
тока. По условию
— искомая скорость возрастания силы
тока. По условию
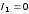 ,
тогда
,
тогда
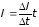
и
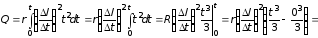
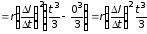 .
.
Таким образом,
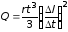 ,
,
откуда
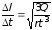 .
.
Вычисление:
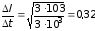 А/с.
А/с.
Ответ:
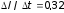 А/с.
А/с.
335. Плоский конденсатор с площадью
пластин S = 300 см2
каждая заряжен до разности потенциалов
U = 1000 В. Расстояние
между пластинами d = 4 см.
Диэлектрик — стекло. Определить энергию
W поля конденсатора
и плотность
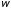 энергии поля.
энергии поля.
Дано:
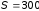 см2
см2
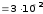 м2
м2
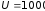 В
В
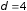 см
см
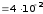 м
м
Найти:
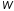 ,
,
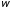 .
.
Решение. Энергия конденсатора равна
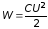 ,
,
где
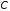 — емкость конденсатора;
— емкость конденсатора;
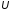 — разность потенциалов между его
пластинами. Емкость плоского конденсатора
равна
— разность потенциалов между его
пластинами. Емкость плоского конденсатора
равна
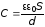 ,
,
где
 — диэлектрическая проницаемость среды,
заполняющей пространство между пластинами
конденсатора;
— диэлектрическая проницаемость среды,
заполняющей пространство между пластинами
конденсатора;
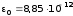 Ф/м — электрическая постоянная;
Ф/м — электрическая постоянная;
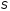 — площадь пластин;
— площадь пластин;
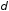 — расстояние между пластинами.
Диэлектрической средой между пластинами
по условию является стекло. Из справочника
узнаем, что
— расстояние между пластинами.
Диэлектрической средой между пластинами
по условию является стекло. Из справочника
узнаем, что
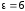 .
Получаем
.
Получаем
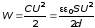 .
.
Вычисление:
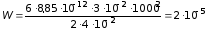 Дж.
Дж.
Плотность энергии по определению равна
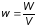 ,
,
где
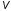 — в данном случае объем конденсатора,
равный
— в данном случае объем конденсатора,
равный
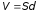 .
Тогда
.
Тогда
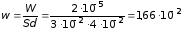 Дж/м3.
Дж/м3.
Ответ:
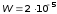 Дж;
Дж;
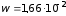 Дж/м3.
Дж/м3.
Задача 10. Кольцо радиусом R
= 10 см находится в однородном магнитном
поле индукцией В =
0,318 Тл. Плоскость кольца составляет угол
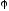 = 30° с линиями индукции. Вычислить
магнитный поток, пронизывающий кольцо.
= 30° с линиями индукции. Вычислить
магнитный поток, пронизывающий кольцо.
Дано:
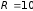 см
см
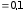 м
м
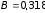 Тл
Тл
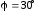
Найти:
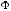 .
.
Решение.

По определению, магнитный поток равен
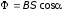 ,
,
где
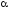 — угол между направлением линий
магнитного поля и нормалью к контуру.
Из рисунка видно, что
— угол между направлением линий
магнитного поля и нормалью к контуру.
Из рисунка видно, что
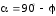 ,
поэтому
,
поэтому
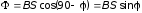 .
.
Площадь кольца равна
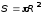 .
.
Тогда
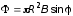 .
.
Подставляя числовые данные, получим
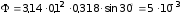 Вб.
Вб.
Ответ:
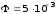 Вб.
Вб.
