
k_r_№1
.pdf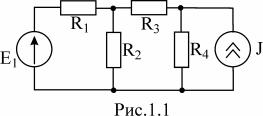
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ №1
Для успешного выполнения и защиты контрольной работы №1 студенту
необходимо изучить и научиться практически применять следующие методы расчета цепей постоянного тока:
1.Метод уравнений Кирхгофа.
2.Метод контурных токов.
3.Метод узловых напряжений.
4.Метод наложения.
5.Метод преобразования (упрощения).
6.Метод эквивалентного генератора напряжения (тока).
7.Топологические методы.
Необходимо научиться определять напряжения на элементах схемы, мощность, отдаваемую или потребляемую источниками энергии, составлять баланс
мощностей и изображать потенциальную диаграмму для замкнутого контура схемы.
1 Определение токов электрической схемы методом уравнений Кирхгофа
Этот метод основан на применении первого и второго законов Кирхгофа, не требует никаких преобразований схемы и пригоден для расчета любой цепи. Количество уравнений, составленных по этому методу, равно количеству неизвестных токов. Положительные направления токов задаются произвольно. Количество уравнений, составленных по первому закону Кирхгофа для цепи, имеющей q - узлов, равно q −1. Недостающее число уравнений составляется
по второму закону Кирхгофа. При выборе контуров по второму закону Кирхгофа нужно придерживаться правила, что каждый из контуров должен отличаться от других хотя бы одной новой ветвью. Такие контуры называются независимыми.
Ветви с источниками тока учитываются только при составлении уравнений по первому закону Кирхгофа и не должны быть включены в выбранные независимые контуры.
ПРИМЕР 1. Определить токи во всех ветвях схемы, если
R1 = R2 = R3 = R4 =10 Ом,
E1 =10 В, J = 2А.
РЕШЕНИЕ. В схеме необходимо задать направление четырех неизвестных токов: (рис.1.2). Схема содержит 3 узла, поэтому по первому закону составим два уравнения (для 2 и 3 узлов).
ìI1 - I2 - I3 = 0 íîI3 - I4 = -J
PDF created with pdfFactory Pro trial version www.pdffactory.com
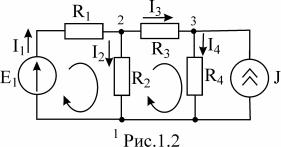
Два недостающих уравнения составим по второму закону Кирхгофа, для чего выберем два контура (см. рис.1.2).
ìI1R1 + I2R 2 = E1
íî- I2R 2 + I3R3 + I4R4 = 0
Подставив численные значения, получим систему из четырех уравнений:
ìI1 - I2 - I3 = 0 ïïI3 - I4 = -2
íï10I1 + 10I2 =10
ïî-10I2 + 10I3 +10I4 = 0
В результате решения системы уравнений получим токи: I1 = 0,2 A; I2 = 0,8 A; I3 = −0,6A; I4 =1,4 A.
Для проверки правильности решения задачи составим баланс мощностей:
PИ = РП ,
где PИ - мощность, отдаваемая источниками;
РП - мощность, потребляемая элементами схемы.
E1I1 + JU31 = I12R1 + I22R2 + I32R3 + I24R4
где U31 - напряжение между узлами 3-1 .
U31 = I4R4 .
Тогда 10 × 0,2 + 21,4 ×10 = 0,04 ×10 + 0,64 ×10 + 0,36 ×10 +10 ×19,6
30 = 0,4 + 6,4 + 3,6+19,6
30 = 30.
2 Метод контурных токов
Метод контурных токов основан на использовании только второго закона Кирхгофа, что позволило уменьшить число уравнений. Достигается это
разделением схемы на независимые контуры и введением для каждого контура своего тока - контурного, являющегося определяемой величиной. Количество уравнений соответствует количеству уравнений, составляемых по второму закону Кирхгофа, и может быть определено из уравнения
K = NB − NY +1− NT ,
где NB - число ветвей;
NY - число узлов;
NT - число ветвей с источником тока.
Контуры, для которых составляются уравнения, не должны содержать ветви с источником тока, но учет падения напряжения от источников тока обязателен. Для этого рекомендуется обозначать контуры, которые содержат источник тока, но только один. В этом случае контурный ток известен и равен по величине
PDF created with pdfFactory Pro trial version www.pdffactory.com
источнику тока. Источник тока не может быть включен в несколько контуров.
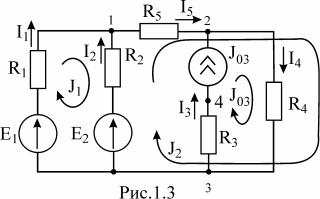
ПРИМЕР 2. Определить токи во всех ветвях схемы (рис.1.3), если
R1 = R2 = R3 = R4 = R5 =10 Ом ,
E1 =10 B, E2 = 50 B, J03 =1A.
РЕШЕНИЕ. Определим количество уравнений по формуле
K = NB − NY +1 − NT = 5 − 3 +1 −1 = 2
Обозначим контурные токи J1,J2 , а также известный контурный ток J03 . Уравнения для определения неизвестных контурных токов J1 иJ2 :
ìJ1(R1 + R2 ) - J2R 2 = E1 - E2
íî- J1R 2 + J2 (R 2 + R5 + R4 ) + J03R4 = E2
Подставим численные значения:
ì 20J1 -10J2 = -40 íî-10J1 + 30J2 = 40,
Откуда J1 = −1,6A ,
J2 = 0,8A .
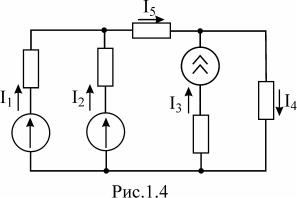
Обозначим токи в ветвях схемы (рис.1.4). Определим токи в ветвях, исходя из известных контурных токов:
I1 = J1 = −1,6 A,
I2 = J2 − J1 = 2,4 A, I3 = J2 = 0,8 A,
I4 = J2 − J03 =1,8 A,
I5 = J2 = 0,8 A.
PDF created with pdfFactory Pro trial version www.pdffactory.com
Контурный ток берётся со знаком плюс, если направление контурного тока и тока в ветви совпадают, и со знаком минус, если токи направлены в разные стороны.
Для проверки правильности решения составим баланс мощностей:
E1I1 + E2I2 + J03U24 = I12R1 + I22R2 + I32R3 + I24R4 + I52R5 ,
U24 = I4R4 + J03R3 = 28 B,
-10 ×1,6 + 50 × 2,4 + 28 ×1 = 25,6 + 57,6 + 6,4 +10 + 32,4, 132 =132.
3 Метод узловых напряжений
Метод основан на использовании первого закона Кирхгофа. Количество уравнений, составляемых по этому методу, определяется из выражения
K = NY −1− NH
где NY - число узлов;
N H - число источников напряжения, включенных между узлами без
сопротивлений.
При составлении уравнений в качестве базисного узла (узел, потенциал, которого принимается равным нулю) целесообразно выбрать тот узел, в котором сходится наибольшее число ветвей. Если в схеме имеется ветвь с источником напряжения без сопротивления, то в качестве базисного выбирают один из тех узлов, к которому присоединена эта ветвь. Если схема содержит две и более подобных ветвей (причем эти ветви не имеют общих узлов), то такую схему необходимо преобразовать.
В результате решения системы узловых уравнений определяются напряжения между узлами схемы. Токи в ветвях находятся с помощью закона Ома. ПРИМЕР 3: а) Определить токи в ветвях схемы (рис.1.5), если
R1 = R2 = R3 = R4 = R5 = R7 =10 Ом;
E1 = 50 B; E3 = 20 B; E7 = E6 = 30 B; J02 = 2 A.
PDF created with pdfFactory Pro trial version www.pdffactory.com

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б) |
|
Построить |
потенциальную |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
диаграмму для |
|
внешнего контура |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
схемы. |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
РЕШЕНИЕ: Определим количество |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
уравнений, необходимых для |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
решения. Для этого обозначим узлы |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
схемы и воспользуемся формулой |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
K = NY −1− NH = 4 −1−1 = 2 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Базисным узлом выберем узел 3, |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
тогда напряжение |
|
|
|
|||||||||
U13 = E6 = 30 B , а уравнения будут иметь вид |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
ì |
æ |
|
1 |
|
|
|
1 |
|
|
|
ö |
|
|
|
|
1 |
|
|
|
|
1 |
|
|
E1 |
|
|
E7 |
|
E3 |
|
||||||
ïU43 |
ç |
|
|
+ |
+ |
|
|
1 ÷ |
- U23 |
|
|
- U13 |
|
= |
|
- |
- |
+ J02 |
||||||||||||||||||
ç |
|
|
|
|
R3 |
|
|
|
÷ |
R7 |
|
R1 |
|
|
R7 |
R3 |
||||||||||||||||||||
ï |
è R1 |
|
|
|
|
R7 ø |
|
|
|
|
|
|
|
R1 |
|
|
||||||||||||||||||||
í |
|
|
1 |
|
|
|
|
æ |
1 |
|
|
|
1 |
|
|
1 |
ö |
|
|
|
|
1 |
|
E7 |
|
|
|
|
|
|||||||
ï |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
ç |
|
|
|
|
|
÷ |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
ï- U |
43 |
|
|
|
|
+ U23ç |
|
|
|
+ |
|
+ |
|
|
|
|
÷ |
- U13 |
|
|
|
= |
|
|
|
- J02 |
|
|
||||||||
|
R7 |
|
|
|
R5 |
|
|
|
|
|
R4 |
R7 |
|
|
|
|||||||||||||||||||||
î |
|
|
|
|
|
|
è R4 |
|
|
|
|
R7 ø |
|
|
|
|
|
|
|
|
|
|||||||||||||||
Подставив численные значения, получим систему 2 линейных уравнений:
ì 0,3U43 - 0,1U23 = 5 íî- 0,1U43 + 0,3U23 = 4
В результате решения определяем узловые напряжения : U43 = 23,75 B;
U23 = 21,75 B; U13 = 30 B.
Вычисляем напряжения между остальными узлами как разность узловых напряжений:
U12 = U13 − U23 = 30 − 21,25 = 8,75 B,
U14 = U13 − U43 = 30 − 23,75 = 6,25 B, U24 = U23 − U43 = 21,25 − 23,75 = −2,5 B.
На основании второго закона Кирхгофа и закона Ома составим уравнения для определения токов в ветвях схемы (рис.1.6)
U14 = I1R1 − E1
отсюда
I1 = (U14 + E1)/R1 = 5,625A, I4 = −U12/R4 = −0,875A, U24 = E7 − I7R7 ,
I7 = (E7 − U24 )/R7 = 3,25A,
PDF created with pdfFactory Pro trial version www.pdffactory.com
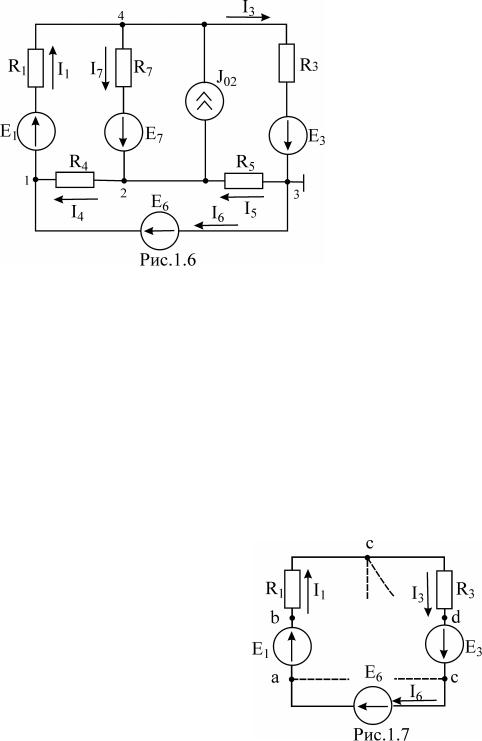
I5 = U23/R5 = 2,125A,
U43 = I3R3 - E3 ,
I3 = (U43 + E3 )/R3 = 4,375A.
На основании первого закона Кирхгофа для узла 1:
I6 = I1 − I4 = 6,5 A.
Правильность решения проверим, составив баланс мощностей :
E1I1 + E7I7 + J02 (-U24 ) + E6I6 + E3I3 = I12R1 + I72R7 + I24R 4 + I52R5 + I32R3 ,
50 × 5,625 + 30 × 3,25 + 2 × 2,5 + 30 × 6,5 + 20 × 4,375 = 5,6252 ×10 + 3,252 ×10 + 0,8752 ×10 + 2,1252 ×10 + 4,3752 ×10, 666,25 = 666,25.
Для построения потенциальной диаграммы необходимо знать напряжение на всех элементах контура, а также сопротивления всех элементов контура. На рис.1.7 показан контур, для которого необходимо построить потенциальную диаграмму.
Базисную точку выберем произвольно, например е. Построение будем производить, обходя контур по часовой стрелке.
Определим потенциалы точек:
ϕa = ϕc + E6 = 30 B, jb = ja + E1 = 80 B,
jc = jb - I1R1 = 80 - 5,625×10 = 23,75B, jd = jc - I3R3 = 23,75 - 4,375×10 = -20 B,
ϕe = ϕd + E3 = −20 + 20 = 0 .
PDF created with pdfFactory Pro trial version www.pdffactory.com
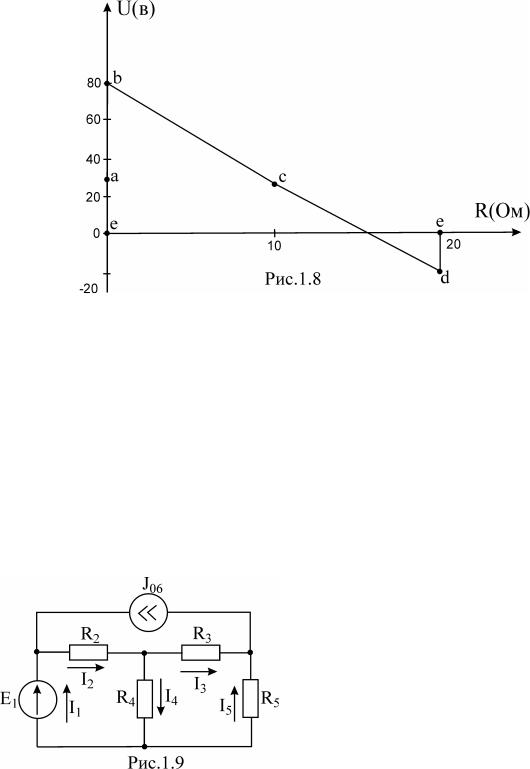
По оси абсцисс будем откладывать значения сопротивлений элементов, а по оси ординат - значения потенциалов точек. Базисную точку помещаем в начало координат (рис.1.8).
4 Метод наложения
Метод основан на том, что в любой линейной электрической цепи токи могут быть получены как алгебраическая сумма токов, вызываемых действием каждого источника энергии в отдельности. Эти токи называются частичными токами.
При определении частичных слагающих токов необходимо учитывать внутреннее сопротивление тех источников энергии, которые принимаются отсутствующими при вычислении слагающих токов. Если в цепи заданы идеальные источники энергии, то при определении токов, вызываемых каким- либо одним источником, все остальные источники напряжения закорачиваются,
а ветви, в которых находятся источники тока - разрываются.
ПРИМЕР 4. Определить токи во всех ветвях схемы (рис.1.9), если
R2 = R3 = R4 = R5 = 10 Ом;
E1 = 10 B; J06 = 1A.
РЕШЕНИЕ 1. Определим частичные слагающие токи, вызываемые источником напряжения E1. Разорвем ветвь с
источником тока. Токи в цепи (рис.1.10) определим методом преобразований. Вычислим сопротивление, эквивалентное сопротивлениям R3; R4 ; R5 :
R354 |
= |
(R3 + R5 ) × R 4 |
= 6,667 Ом |
|
|||
|
|
R3 + R5 + R4 |
|
PDF created with pdfFactory Pro trial version www.pdffactory.com
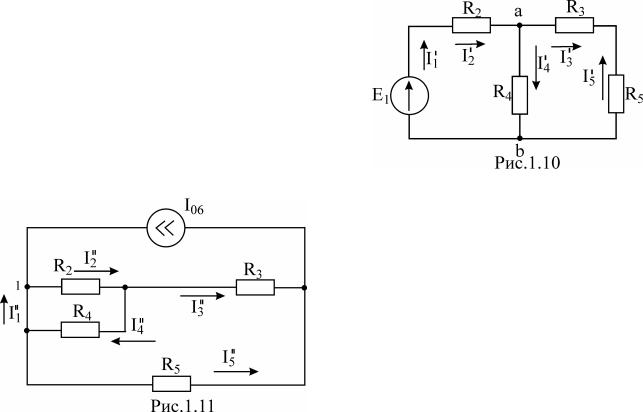
тогда
I1' = I'2 = E1/(R 2 + R354 ) =10/(10 + 6,667) = 0,6 A.
Определим напряжениеU'ab
U'ab = I1' R354 = 4 B, тогда
I'4 = U'ab /R 4 = 0,4 A,
I3' = -I5' = Uab /(R3 + R5 ) = 0,2 A.
2. Определим частичные слагающие токи, вызываемые источником тока J06 . Закоротим
ветвь, где находится E1 (это равносильно
равенству нулю внутреннего сопротивления данного источника) (рис.1.11).
Сопротивления включены параллельно, заменим их
сопротивлением
R 24 = R 2R 4/(R 2 + R 4 ) = 5 Ом .
Определим токи I3'' и I5'' по правилу
плеч:
\
I3'' = J06 × R5/(R 24 + R3 + R5 ) = 0,4 A,
I5'' = J06 × (R 24 + R3 )/(R 24 + R3 + R5 ) = = 0,6 A.
Аналогично определим токи I'2' и I'4' :
I'2' = I3'' × R4/(R4 + R2 ) = 0,2 A, I'4' = -I3'' × R2/(R4 + R2 ) = -0,2 A.
Для узла 1 составим первое уравнение Кирхгофа и определим ток I1''
I1'' = I'2' - J06 = -0,8 A,
3. Найдем искомые токи в ветвях схемы (см.рис.1.9) как алгебраическую сумму
частичных слагающих токов
I1 = I1' + I1'' = -0,2 A,
I2 = I'2 + I'2' = 0,8 A,
I3 = I3' + I3'' = 0,6 A,
I4 = I'4 + I'4' = 0,2 A,
I5 = I5' + I5'' = 0,4 A.
PDF created with pdfFactory Pro trial version www.pdffactory.com
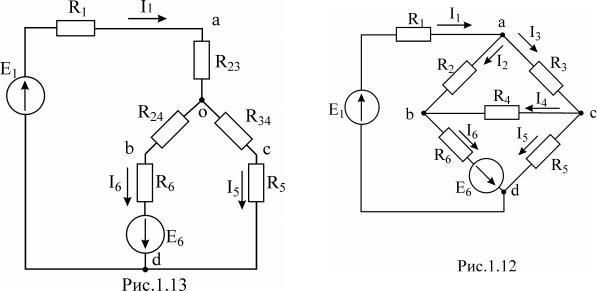
Правильность решения проверим, составив баланс мощностей:
E1I1 + J06 (I2R 2 + I3R3 ) = I22R 2 + I32R3 + I24R 4 + I52R5
где I2R 2 + I3R3 - напряжение на зажимах источника тока J06 .
- 0,2 ×10 +1(0,8 ×10 + 0,6 ×10) = 0,82 ×10 + 0,62 ×10 + 0,2 ×10 + 0,42 ×10
PИСТ = PНАГР
В данном случае источник тока J06 отдает энергию в схему (его мощность больше нуля).
PT = J06 (I2R2 + I3R3 ) =14 Вт .
а источник напряжения E1 потребляет энергию (его мощность отрицательна)
PH = E1J1 = −2 Вт .
5 Метод преобразования
Суть метода заключается в преобразовании электрической схемы различными методами с целью уменьшения числа ветвей и узлов, а значит, и количество уравнений, определяющих электрическое состояние схемы.
Во всех случаях преобразования заданных электрических схем эквивалентными схемами другого вида необходимо выполнять условия неизменности токов и напряжений в тех частях схемы, которые не затронуты преобразованием.
ПРИМЕР 5. Определить токи в ветвях схемы (рис.1.12), если
E1 = E6 = 40 B;
R1 = R6 = R5 =10 Ом;
R2 = R3 = R4 = 30 Ом.
PDF created with pdfFactory Pro trial version www.pdffactory.com
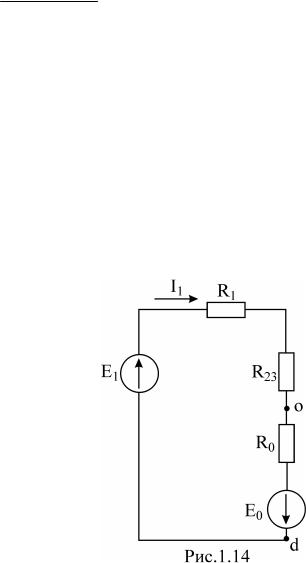
РЕШЕНИЕ. Преобразуем треугольник R2 ,R3 ,R 4 в звезду, на основании
следующих формул (рис.1.13):
R 23 |
= |
|
R 2R3 |
|
R 2 |
+ R3 + R 4 |
|||
|
|
|||
R34 |
= |
|
R3R 4 |
|
R 2 |
+ R3 + R 4 |
|||
|
|
|||
R 24 |
= |
|
R 2R 4 |
|
R 2 |
+ R3 + R 4 |
|||
|
|
= |
30 × 30 |
|
=10 Ом, |
30 + 30 + |
30 |
=10 Ом,
=10 Ом.
Обозначим последовательно включенные сопротивления
R246 = R6 + R 24 = 20 Ом
и сопротивления R345 = R5 + R34 , объединим две ветви (od и oc ), включенные
параллельно, в одну. Общее сопротивление:
|
R0 = |
|
R 246R345 |
|
=10 Ом. |
|
||||||||
|
|
R 246 + R345 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
||||||
Общий источник напряжения: |
|
|
|
|
||||||||||
|
E0 = |
|
|
1/R 246 |
× E6 |
|
= 20 B. |
|||||||
|
1/R 246 + |
|
|
|
|
|
||||||||
|
|
|
1/R 345 |
|
||||||||||
Преобразованная схема показана на рис.1.14: |
||||||||||||||
I1 = |
|
E1 + E0 |
|
= |
|
|
40 + 20 |
|
= 2 A. |
|||||
R1 |
+ R 23 + R0 |
10 |
+ 10 + 10 |
|
||||||||||
|
|
|
|
|||||||||||
Определим напряжение Uod : |
|
|
|
|
|
|||||||||
|
|
|
|
|
Uod = I1R0 - E0 = 2 ×10 - 20 = 0 B. |
|||||||||
Напряжение Ude |
|
на схеме (рис.1.13) позволяет определить ток I5 = 0 A и ток |
||||||||||||
I6 : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I6 (R24 + R6 ) − E6 = Ude = 0,
I6 = E6/(R 26 + R6 ) = 40/(10 +10) = 2 A.
На этой же схеме определим напряжения Uac , Uab иUcb :
Uac = I1R 23 + I5R34 = 2 ×10 - 0 = 20 B,
Uab = I1R 23 + I6R 24 = 2 ×10 + 2 ×10 = 40 B, Ucb = I6R 24 - I5R34 = 20 B.
PDF created with pdfFactory Pro trial version www.pdffactory.com
