
тэц
.pdf
|
|
|
|
|
|
|
|
Zг |
|
|
|
|
|
I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Uг |
|
|
|
Eг |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Zг |
|
|
U0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
U |
|
|
2 |
|
|
|
|
U 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
S m = |
U |
0 I = I |
|
|
Z |
г |
= |
|
|
|
|
г |
|
Z |
г = |
|
|
г |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2Z г |
|
|
|
|
4Z г |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Рабочая мера передачи определяется в виде: G |
p |
= |
1 |
ln |
|
U 0 I |
= |
|
1 |
ln |
S m |
= A + jB . |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
U |
2 I 2 |
2 |
|
|
|
S 2 |
|
|
p |
p |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U г2 Z н |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
Ap |
= |
1 |
ln |
|
S m |
|
|
= |
1 |
ln |
|
|
|
|
= ln |
|
|
U |
г |
|
|
+ |
|
1 |
ln |
|
Z н |
|
|
– |
рабочее ослабление (Нп). |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
4U22 Z г |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
2 |
|
S 2 |
|
|
|
|
|
2 |
|
|
|
|
|
2U 2 |
|
|
|
2 |
|
|
Z г |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
U |
|
|
|
|
|
|
|
|
|
Z н |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
A = 20 lg |
|
|
|
г |
|
|
|
+10 lg |
|
|
|
– |
рабочее ослабление (дБ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
p |
|
|
|
|
|
|
|
2 |
U |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z г |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
Теоретически рабочее ослабление вычисляют по формуле: Ap |
= Ac + DA1 + DA2 + DA3 , где Ac |
– |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
характеристическое ослабление ЧП; DA1 , DA2 |
– |
дополнительные ослабления, связанные из-за |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
несогласованности на входе и выходе ЧП: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z c1 + Z г |
|
|
|
|
|
Z c2 + Z н |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
DA = 20 lg |
|
|
, DA = 20 lg |
|
|
. |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
2 |
|
Z c1 Z г |
|
|
|
2 |
|
|
|
|
|
2 |
|
Z c2 Z н |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
DA3 – дополнительное ослабление |
за |
счёт |
многократного |
отражения |
энергии от входных |
и |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
выходных зажимов ЧП: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z c1 - Z г |
|
Z c2 - Z н |
e−2Γс |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
DA = 20 lg |
1- |
× |
. |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Z c1 |
+ Z г Z c2 + Z н |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
При полном согласовании: Ap = Ac . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
Рабочее ослабление является вещественной частью рабочей меры передачи: |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Gр = Ap + jBp , где Bp |
– рабочая фаза. |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Рабочая передаточная функция определяется в виде: T p = 2 |
U 2 |
|
|
Z г |
. |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
U г |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z н |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Т.к. A = ln |
|
U |
г |
|
|
+ |
1 |
ln |
Z н |
|
|
, то легко установить следующую связь: A = ln |
|
1 |
. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
p |
|
|
|
2U 2 |
2 |
|
|
|
|
Z г |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
T p |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вывод: к рабочим параметрам ЧП относят:
1.Входное сопротивление Z вх ;
2.Рабочее ослабление Ap ;
3.Рабочая мера передачи Гр ;
4.Рабочая фаза Вр ;
5.Рабочая передаточная функция T p ;
Характеристические параметры Г – образного четырёхполюсника.
|
Z1 |
T - вход |
Z2 П - вход |
Характеристические сопротивления:

Z c1 = 
 Z1X Z1K , Z c2 =
Z1X Z1K , Z c2 = 
 Z 2X Z 2K .
Z 2X Z 2K .
Z 1X = Z 1 + Z 2 , Z1K = Z1 .
Z 2X |
= Z 2 , Z 2K = |
Z1 Z 2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
Z1 + Z 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Отсюда получаем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z1 Z 2 |
|
|
|
|
|
|
Z1 Z 2 |
|
|
||||||||||||||||||
|
|
|
Z c1 = Z1 (Z1 + Z |
2 ) = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
Z1 Z |
2 1+ |
|
= Z T |
, Z c2 |
= |
|
|
Z 2 |
= |
|
|
|
|
= Z П . |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z 2 |
|
|
|
|
Z1 + Z 2 |
|
|
|
|
1+ |
Z1 |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z 2 |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Определим характеристическую меру передачи через A – |
параметры: |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
chGc = |
|
|
|
|
|
|
|
|
|
= |
|
|
, где |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
A11 A22 , shГc |
A12 A21 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
A11 |
= 1+ |
Z1 |
, A12 = Z1 , A21 = |
1 |
, A22 = 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
Z 2 |
|
Z 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
После подстановки получаем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
= 1+ |
|
×1 = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
chГc |
|
Z1 |
1+ |
Z1 |
|
, shГc |
= Z1 |
1 |
|
= |
|
Z1 |
. |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Z 2 |
|
|
|
|
|
Z 2 |
|
|
|
|
|
|
|
Z 2 |
|
Z 2 |
|
|
|
|
|
|
|||||||||||
Выучить формулы для Г-образного ЧП:
|
|
|
|
Z1 |
|
|
|
|
|
|
|
|
|
Z1 |
|
|
|
Z1 |
|
|
|
Z T = |
|
+ |
|
Z П = |
Z1 Z 2 |
|
= 1+ |
|
, shГc = |
|
|
||||||||||
Z1 Z |
2 1 |
|
, |
, chГc |
|
. |
|||||||||||||||
|
|
||||||||||||||||||||
|
|
|
|
||||||||||||||||||
|
|
|
|
Z 2 |
|
|
1+ |
Z1 |
|
|
|
|
Z 2 |
|
|
|
Z 2 |
||||
|
|
|
|
|
Z 2 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Характеристические параметры Т – образного четырёхполюсника. Т-образный ЧП может быть составлен следующим образом:
|
|
Z1 |
|
|
|
|
|
|
Z1 |
|
|
|
|
Z1 |
|
Z1 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ZТ |
|
|
|
|
|
|
|
|
|
|
ZТ |
|
Z ’ |
|
Z |
2 |
|
|
Z ’ |
|||
|
|
Z2 |
|
|
|
|
Z2 |
|
|
|
Т |
|
|
|
|
Т |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||
Поскольку Г-образные ЧП соединены согласованно и регулярно, то характеристические параметры Т-образного ЧП определяются как:
|
¢ |
|
|
|
|
|
|
|
Z1 |
|
′ |
|
|
|
|
|
Z |
T = Z Т |
= Z1 Z |
2 1 |
+ |
|
|
, G с = 2Gс . |
|
||||||
|
Z 2 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
|
¢ |
|
|
|
|
2 |
|
|
shГc = |
|
Z1 |
|
|
|
|
|
Z |
1 |
||
Поскольку chГ c = ch2Gс |
= 1+ 2sh |
|
Gс |
, а |
|
|
|
, то |
chГ c = 1 |
+ 2 |
|
|
|||
|
|
Z 2 |
|
Z 2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Выучить формулы для Т-образного ЧП:
|
|
|
|
|
|
|
|
|
|
|
¢ |
|
|
|
|
|
|
|
Z1 |
¢ |
|
|
Z |
1 |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
Z |
|
Т = |
Z1 Z 2 1+ |
|
|
|
, chГ c = 1 |
+ 2 |
|
|
|
. |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
Z 2 |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z 2 |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¢ |
|
|
|
|
|
|
|
|
|
|
|
|
|
Z1 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Поскольку ЧП симметричный, то ch |
Г c = |
|
A11 A22 |
= A11 = 1+ |
2 |
|
|
|
. |
|
|
|
|
|
||||||||||||||||||||||||||
|
Z 2 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Характеристические параметры П – |
образного четырёхполюсника. |
||||||||||||||||||||||||||||||||||||||
П-образный ЧП может быть составлен следующим образом: |
|
|
|
2Z1 |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
Z1 |
|
|
|
|
|
|
|
|
Z1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ZП |
|
Z2 |
|
ZТ |
|
|
|
|
|
ZТ |
Z2 |
|
|
|
ZП |
|
Z2 |
|
|
|
|
|
Z2 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

Аналогично, как и для Т-образного ЧП можно показать, что характеристические параметры определяются в виде:
′ |
|
Z |
1 Z |
2 |
|
′ |
|
Z1 |
|
|
Z П = Z П |
= |
|
|
|
|
|
, chГ c =1 |
+ 2 |
|
. (Формулы выучить!) |
1+ |
Z |
1 |
Z 2 |
|||||||
|
|
Z 2 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||
Четырёхполюсники Г, Т и П-образного типов образуют класс лестничных схем
Z1 |
|
Z1 |
|
Z1 |
2Z1 |
|||||||||
|
|
|
|
|
|
Z2 |
|
|
|
|
|
|
|
|
|
|
Z2 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
Z2 |
|
|
Z2 |
|||||
|
|
|
|
2 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Последние 3 схемы находят широкое применение в электрических фильтрах.
Лекция 9
|
|
|
|
|
|
|
|
|
|
Аналоговые частотно-избирательные фильтры. Определение и классификация |
|||||||||||||||||||||||||||||||||||||
|
|
|
Электрический |
фильтр – |
|
|
четырёхполюсник, пропускающий без заметного ослабления |
||||||||||||||||||||||||||||||||||||||||
колебания определённых частот и подавляющий колебания других частот. |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
Классификация фильтров. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
1. |
|
|
|
|
|
По расположению полосы пропускания (ПП) и полосы задерживания (ПЗ). |
|||||||||||||||||||||||||||||||||||||||||
A, дБ |
|
|
|
|
|
|
|
|
|
|
ФНЧ − фильтр нижних частот |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
Amin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ПЗ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
fс |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
ПП |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f1=0 |
|
|
|
f2 |
|
|
|
f3 |
|
|
f4→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
Ω1=0 Ω2 |
|
Ω3 |
|
|
Ω4 |
→∞ |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
f1 |
– нижняя граничная частота ПП [Гц]; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
f2 |
– |
верхняя граничная частота ПП [Гц]; |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
f3 |
– |
нижняя граничная частота ПЗ [Гц]; |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
f4 |
– |
верхняя граничная частота П3 [Гц]; |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
Ω1 |
– |
нормированная нижняя граничная частота ПП; |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
Ω2 |
|
– |
|
нормированная верхняя граничная частота ПП; |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
Ω3 |
– |
нормированная нижняя граничная частота ПЗ; |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
Ω4 |
|
– |
|
нормированная верхняя граничная частота ПЗ; |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
fс |
|
– |
|
частота среза [Гц] (Ослабление равно 3 дБ) |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
Amin |
– |
минимальное допустимое ослабление в ПЗ; |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
A – |
|
максимальное допустимое ослабление в ПП; |
|
|
< f < f3 , или Ω2 < Ω < Ω3 . Нормирование у |
||||||||||||||||||||||||||||||||||||||||||
Переходной областью называют диапазон частот: |
f2 |
||||||||||||||||||||||||||||||||||||||||||||||
ФНЧ по частоте проводят относительно верхней граничной частоты ПП f2 . |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ω = |
f1 |
= 0 , Ω |
2 |
= |
f2 |
=1 , Ω |
3 |
= |
f3 |
, Ω |
4 |
= |
f4 |
= ∞. |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
f2 |
|
|
|
f2 |
|
|
f2 |
|
f2 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
При расчёте фильтров по рабочим параметрам никаких требований к переходной области не предъявляются.
Существуют также: ФВЧ – фильтр верхних частот, ПФ – полосовой фильтр, ЗФ – заграждающий фильтр, ГФ – гребенчатые фильтры (многополосные):
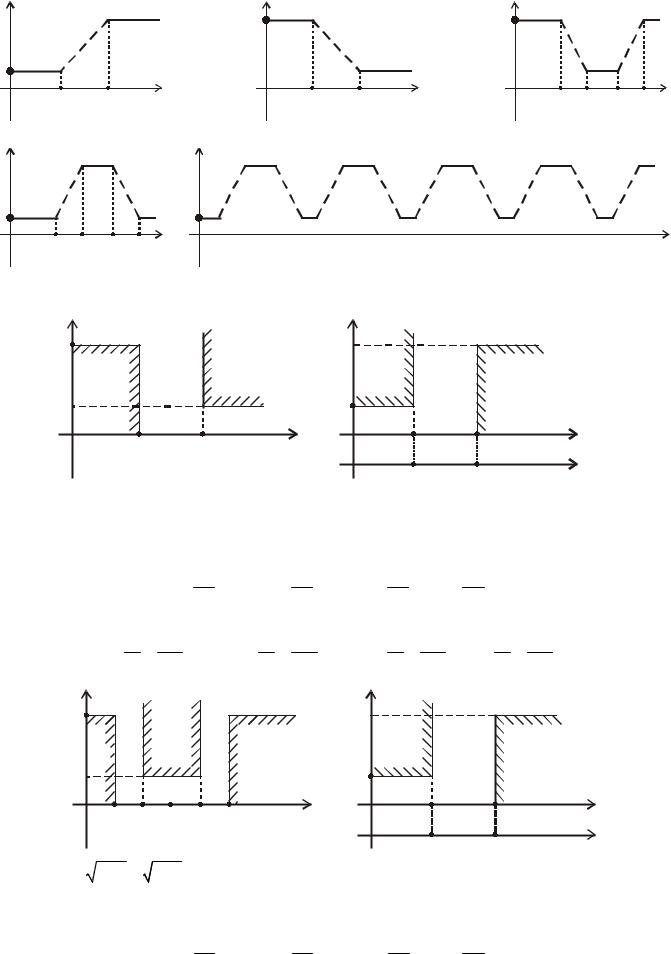
A |
|
|
|
|
|
|
|
A |
|
|
|
|
A |
|
|
|
|
|
|
f |
2 |
f |
3 |
|
f |
|
f |
3 |
f |
2 |
f |
|
f’ |
f’ |
f’’ |
f’’ |
f |
|
|
|
|
|
|
|
|
|
|
3 |
2 |
2 |
3 |
|
||||
A |
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
f’ |
f’ |
|
f’’ |
f’’ |
f |
0 |
f1 |
|
|
2f1 |
3f1 |
|
4f1 |
|
|
f |
|
|
2 |
3 |
|
3 |
2 |
|
|
|
|
|
|
|
||||||
|
|
Самостоятельно!!! Дайте определение каждому из перечисленных фильтров. |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
Фильтр-прототип |
|
|
|
|
|
|
||||
|
A, дБ ФВЧ − фильтр верхних частот |
|
A, дБ ФНЧ − фильтр нижних частот, прототип |
|
|
|||||||||||||
|
Amin |
|
|
|
|
|
|
|
Amin |
|
|
|
|
|
|
|
|
|
|
|
|
ПЗ |
|
|
|
|
|
|
|
|
ПЗ |
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
A |
|
ПП |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ПП |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f4=0 |
f3 |
|
f2 |
f1→∞ |
|
fп1=0 fп2 |
fп3 |
fп4→∞ |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
Ωп1=0 Ωп2 |
Ωп3 |
Ωп4→∞ |
|
|
|
|||
fp1 , |
fp2 , |
fp3 , |
fp4 – |
граничные частоты ФНЧП [Гц]. Для ФНЧП справедливы соотношения: |
|
|
||||||||||||
|
|
|
|
|
|
|
|
fp1 = f4 , fp2 = f3 , fp3 = f2 , fp4 = f1 . |
|
|
|
|
|
|||||
Ωp1 , Ωp2 , Ωp3 , Ωp4 |
– нормированные граничные частоты ФНЧП. |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
Ωp1 |
= fp1 = 0 , Ωp2 = fp2 = 1 , Ωp3 |
= fp3 , Ωp 4 |
= fp4 = ∞ . |
|
|
|
|
|
||||
|
|
|
|
|
|
|
fp2 |
fp2 |
|
|
|
fp 2 |
fp 2 |
|
|
|
|
|
Для перехода обратно к схеме ФВЧ используются соотношения: |
|
|
|
|
|
|
||||||||||||
|
|
Ω = f1 |
= |
1 |
= ∞ , Ω |
2 |
= |
f2 = |
1 |
= 1 , Ω |
3 |
= f3 = |
1 , Ω |
4 |
= f4 = |
1 |
= 0 . |
|||||||||
|
|
1 |
f2 |
|
Ωp1 |
|
|
|
|
|
f2 |
Ωp 2 |
|
|
f2 |
Ωp3 |
|
f2 |
Ωp4 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
A, дБ ПФ − полосовой фильтр |
|
|
A, дБ фильтр нижних частот, прототип |
||||||||||||||||||||||
|
Amin |
|
|
|
|
|
|
|
|
|
|
|
|
|
Amin |
|
|
|
|
|
|
|
|
|
|
|
|
|
ПЗ |
|
|
|
|
|
|
|
|
|
|
ПЗ |
|
|
|
|
|
|
|
|
|
ПЗ |
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
ПП |
|
|
|
|
|
|
|
|
|
ПП |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
f’ =0 |
f’ |
|
f’ |
f |
|
f |
|
f |
|
|
|
f →∞ |
|
|
f |
=0 f |
|
|
|
f |
|
f |
→∞ |
||
|
4 |
|
0 |
2 |
3 |
|
|
|
п2 |
|
|
|
||||||||||||||
|
|
3 |
|
2 |
|
|
|
|
4 |
|
|
|
|
п1 |
|
|
|
п3 |
|
|
п4 |
|||||
|
= f1 = f1′ = |
f2 f2′ = |
|
f3 f3′ |
|
|
|
|
|
|
|
|
|
|
Ωп1=0 Ωп2 |
|
|
Ωп3 |
|
Ωп4→∞ |
||||||
f0 |
|
– |
центральная (среднегеометрическая) частота [Гц]. |
|
|
|||||||||||||||||||||
Для ФНЧП справедливы следующие соотношения: |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
fp1 = f1 − f1′ = 0 , fp2 = f2 − f2′ , fp3 = f3 − f3′ , fp4 = f4 − f4′ = ∞ . |
|
|
|||||||||||||||||||||
|
|
|
|
|
Ωp1 = fp1 = 0 , Ωp2 = fp2 = 1 , Ωp3 |
= fp3 , Ωp4 = fp 4 = ∞ . |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
fp2 |
|
|
|
|
|
fp2 |
|
|
|
fp2 |
|
|
fp2 |
|
|
|
||
Для ПФ выполняются соотношения: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||

W = |
f1 |
|
= 1, W = |
f1 |
= 1, W = |
1 |
, W |
2 |
= |
f2 |
, W¢ |
= |
|
f2′ |
, W |
2 |
= |
1 |
. |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
1 |
|
f0 |
|
|
1 |
|
f0 |
|
|
|
1 |
W1¢ |
|
|
f0 |
|
2 |
|
|
f0 |
|
|
W¢2 |
|||||||||||
|
|
|
|
|
|
|
f3′ |
|
|
|
|
|
|
|
|
|
|
f4′ |
|
|
|
|
||||||||||||||
W |
3 |
= |
f3 |
|
, W¢ |
= |
, W |
3 |
= |
1 |
, W |
4 |
= |
f4 |
= ¥ , W¢ |
= |
= 0 , W |
4 |
= |
1 |
. |
|||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
f0 |
3 |
|
f0 |
|
|
W¢3 |
|
|
|
f0 |
|
|
|
|
4 |
|
f0 |
|
|
|
|
|
W¢4 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Для перехода от ФНЧП к схеме ПФ и обратно используются соотношения:
|
|
|
|
|
|
|
1 |
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(Wp a + |
2 |
2 |
+ 4 ) , |
||||||
|
|
|
|
|
Wp |
= |
|
W - |
|
|
, W = |
|
a |
Wp |
|||
|
|
|
|
|
a |
|
2 |
||||||||||
|
f2 − f2′ |
|
f3 − f3′ |
|
|
|
|
W |
|
|
|
|
|
|
|||
где a = |
= |
|
– коэффициент преобразования. |
|
|
|
|
||||||||||
f0 |
f0 |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2.По использованию элементов
- |
LC-фильтры (содержат индуктивности и ёмкости) |
- |
RC-фильтры (содержат резисторы и ёмкости) |
-Резонаторные фильтры
- |
ARC-фильтры (активные фильтры содержат усилительные элементы) |
3.Классификация по схемам
-Лестничные (цепочные) фильтры
-Мостовые фильтры
-Фильтры с цепями обратной связи
|
|
|
|
|
|
|
|
|
Лестничные LC – фильтры |
|
|
|
|
|
|
|
|||||||||||||||
|
Лестничные LC – |
фильтры – |
это фильтры из каскадно соединенных Г, |
Т и П-образных |
|||||||||||||||||||||||||||
реактивных четырёхполюсников. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2Z1 |
||||||||||||
|
|
Z1 |
|
|
Z1 |
|
Z1 |
|
|
|
|
|
|
Z1 |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
Z2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z2 |
|
|
|
|
|
|
|
|
|
Z2 |
Z2 |
|
|
|
Z2 |
|||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
полузвено с Т-входом |
|
|
звено с Т-входом |
полузвено с П-входом |
звено с П-входом |
||||||||||||||||||||||||||
Собственная мера передачи звеньев Т и П типа определяется: |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
chГ |
c |
= 1+ 2 |
Z1 |
, где G |
|
= А + jB . |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
с |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Z 2 |
|
|
|
с |
c |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
С другой стороны: ch ( Ac + jBc ) = chAc cos Bc + jshAc sin Bc . |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Поскольку Z1 и Z 2 реактивные сопротивления, тоchAc |
cos Bc |
= 1+ 2 |
Z1 |
, shAc sin Bc |
= 0 . |
|
|
||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z 2 |
|
|
|
|
|
|
|
||
Вполосе пропускания (ПП) ослабление равно нулю, поэтому shAc = 0 , sin Bc ¹ 0 .
Вполосе задерживания (ПЗ) ослабление отлично от нуля, следовательно shAc ¹ 0 , sin Bc = 0 .
Для определения граничных частот ПП выполняются условия shAc = 0 |
, sin Bc = 0 . |
||||||
В (ПП) так как A = 0 , то chA = 1, отсюда следует cos B = 1+ 2 |
Z1 |
, −1 |
≤ 1+ 2 |
Z1 |
≤ 1 . |
||
|
|
||||||
c |
c |
c |
Z 2 |
|
|
Z 2 |
|
|
|
|
|
|
|
||
Из последнего неравенства следует, что реактивные сопротивления в (ПП) не могут быть одного знака, т.е. одно из них имеет индуктивный характер, другое – ёмкостной.
-2 £ -2 |
Z1 |
|
|
£ 0 или 1 ³ |
Z1 |
|
³ 0 определяет полосу пропускания. |
||||||||
Z 2 |
Z 2 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
Z1 |
|
= 0 , |
|
|
Z1 |
|
|
= 1 определяют частоты среза |
||||
|
|
|
|
|
|
|
|
||||||||
|
|
|
Z 2 |
Z 2 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|||||||
В полосе задерживания sin Bc |
= 0 , то есть cos Bc принимает значения ±1, поэтому |
||||||||||||||
|
|
Z1 |
|
|
|||||||||||
Bc = ±p , |
chAc = 2 |
|
|
-1 определяет полосу задерживания. |
|||||||||||
Z 2 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||

|
Фильтры нижних частот (ФНЧ) типа «к». Частотные зависимости ослабления, фазы и |
|
||||||||||||||||||
|
|
|
|
характеристических сопротивлений. |
|
|
|
|
|
|
|
|
|
|||||||
|
Для фильтров типа «к» выполняется условие: |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
Z1 Z 2 = k 2 , где |
|
|
|
|
|
|
|
|
|
|
|
||
k – |
вещественное число, |
не |
зависящее |
от |
частоты, |
следовательно двухполюсники |
Z1 и |
Z 2 |
||||||||||||
являются обратными. Рассмотрим ФНЧ типа «к». Г-образное полузвено, Т и П-образные звенья |
||||||||||||||||||||
этого фильтра представим в следующем виде: |
|
|
|
2L |
|
|
|
|
|
|
|
|||||||||
|
L |
|
|
|
|
L |
|
L |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
C |
|
|
|
|
2C |
|
|
C |
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для этих фильтров: Z |
1 |
= jωL , Z |
2 |
= |
1 |
. Произведение сопротивлений: Z |
1 |
Z |
2 |
= L |
= R2 . |
|
|||||||
|
|
|
|
|
jωC |
|
|
|
|
|
|
|
|
C |
0 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
R = |
L = k – номинальное сопротивление фильтра. Определим граничные частоты ПП. |
|
||||||||||||||||||
0 |
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z1 |
|
2 |
Z1 |
|
ω2 |
f 2 |
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
Z 2 = −ω LC , Z 2 |
|
= ω02 = |
f02 , где ω0 = |
LC , f0 = |
2π |
LC . |
|
|
|
|
|
|
|||||||
Первая граничная частота ПП получается из выражения: |
Z1 |
= 0 , откуда |
f |
= 0 . |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
Z 2 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вторая граничная частота ПП получается из выражения: |
Z1 |
=1 , откуда |
f2 |
= f0 . |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
Z 2 |
|
|
|
|
|
|
|
|
|
|
Полоса пропускания (ПП) находится в диапазоне частот: [0, f0 ]. f0 = fc – |
частота среза. |
|
|
|||||||||||||||||
В (ПП) собственное ослабление фильтра Ac = 0 , а собственная фаза определяется выражением: |
|
|||||||||||||||||||
|
cos B |
=1+ 2 Z1 =1− 2 f 2 . (изменяется от 0 до π) |
|
|
|
|
|
|
|
|||||||||||
|
|
|
c |
|
Z 2 |
|
f02 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ac |
|
|
|
|
|
|
Bc |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
fс |
|
|
|
|
f |
0 |
|
fс |
|
|
|
|
|
|
f |
|
|
|
Собственные сопротивления фильтров сильно изменяются с частотой: |
|
|
|
|
|
|
|
|
|
|||||||||||
Z T = |
Z1 Z |
|
Z |
|
|
= R0 |
1− |
f 2 |
|
Z |
|
Z |
2 = |
R |
= |
R |
|
2 1+ |
|
1 |
|
|
2 = R0 1−Ω2 , Z П = |
|
1 |
|
0 |
0 . |
|||||||
|
|
|
Z 2 |
|
|
f |
0 |
|
1+ Z1 |
− |
f 2 |
1−Ω2 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Z |
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
f0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Построим графики частотной зависимости собственных сопротивлений. |
|
|
|
||||||||||||||
|
ZT |
|
|
|
|
|
|
|
|
ZΠ |
|
|
|
|
|
|
|
|
|
В ПП |
|
|
|
В ПЗ |
|
|
|
|
|
|
|
|
|
||
|
|
ZT веществ. |
ZT мнимое. |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
В ПП |
|
|
|
В ПЗ |
|
|
|
|
|
|
|
|
|
|
|
|
|
ZΠ веществ. |
ZΠ мнимое. |
|
|||||
|
|
Ω=0 |
|
|
|
Ω=1 |
|
Ω |
Ω=0 |
|
|
Ω=1 |
|
|
Ω |
||

Фильтры верхних частот (ФВЧ) типа «к». Частотные зависимости ослабления, фазы и характеристических сопротивлений.
|
C |
|
|
|
|
C |
|
|
|
C |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
|
C |
|
|
|
|
L |
2 |
|
L |
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||
Для этих фильтров: Z |
|
= |
1 |
|
|
, Z |
|
= jωL . Произведение сопротивлений: Z |
|
Z |
|
= |
L |
= R2 . |
||||||||||||||||||||||||||||||||||||
1 |
jωC |
2 |
1 |
2 |
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
0 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Определим граничные частоты ПП. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
Z1 |
= − |
|
|
1 |
|
, |
|
|
Z1 |
|
|
= |
ω02 |
= |
|
f02 |
, где ω = |
|
|
|
1 |
|
|
, |
f |
|
= |
|
1 |
|
. |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
Z 2 |
|
ω2 LC |
Z 2 |
|
|
|
|
f 2 |
0 |
|
|
|
|
LC |
|
|
|
0 |
|
2π LC |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
Z1 |
|
= 0 , откуда |
|
= ∞ . |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
Первая граничная частота ПП получается из выражения: |
|
f |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z 2 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
Z1 |
|
=1 , откуда |
|
= f0 . |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
Вторая граничная частота ПП получается из выражения: |
|
f2 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
Z 2 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Полоса пропускания (ПП) находится в диапазоне частот: [ f0 , ∞]. |
f0 = fc – |
частота среза. |
|
|||||||||||||||||||||||||||||||||||||||||||||||
В (ПП) собственное ослабление фильтра Ac |
= 0 , а собственная фаза определяется выражением: |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
cos B |
=1+ 2 |
Z1 |
=1− 2 |
f02 |
. (изменяется от – π до 0) |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
Z 2 |
|
|
|
|
f 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Ac |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Bc |
|
|
|
|
|
|
|
fс |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
0 |
|
|
|
|
fс |
|
|
|
|
|
|
|
f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Собственные сопротивления фильтров изменяются с частотой:
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Z T = |
|
+ |
Z |
1 |
= R0 |
1− |
f |
= R0 1− |
1 |
, Z П = |
Z |
1 |
Z |
2 |
= |
|
R |
|
|
= |
|
R |
|||||||||||
Z1 Z |
2 1 |
|
|
|
0 |
|
|
|
|
0 |
|
|
|
|
0 |
|
. |
||||||||||||||||
|
|
|
2 |
Ω |
2 |
|
|
Z1 |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
Z 2 |
|
|
f |
|
|
|
|
|
|
|
|
|
|
f |
2 |
|
|
|
|
1 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
1+ Z 2 |
|
1− |
0 |
|
|
1− |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ω2 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
2 |
|
|
|||||||||||||
ZT |
|
|
|
В ПЗ |
|
В ПП |
|
ZT мнимое. |
ZT веществ. |
||
Ω=0 |
Ω=1 |
Ω |
|
ZΠ |
|
|
|
В ПЗ |
|
В ПП |
|
ZΠ мнимое. |
ZΠ веществ. |
||
Ω=0 |
Ω=1 |
Ω |
|
Полосовые фильтры (ПФ) типа «к». Частотные зависимости ослабления, фазы и характеристических сопротивлений.
L1 C1
C2 
 L2
L2
Самостоятельно построить!!! Т и П-образный полосовой фильтр
Для данного фильтра имеем: Z |
|
= jωL + |
1 |
, Z |
|
= |
1 |
= |
|
1 |
|
. |
1 |
jωC1 |
2 |
|
|
|
|
||||||
|
1 |
|
|
Y 2 |
|
|
1 |
|
||||
|
|
|
|
|
|
jωC2 |
+ jωL |
|
||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|

Определим произведение этих сопротивлений:
|
|
|
|
|
|
|
|
|
|
wL1 |
- |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1- |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1- w012 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
wC1 |
|
|
|
|
|
|
wL1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
L1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|||||||||||||||||||||||||||||||||||||
Z |
Z |
|
|
|
= |
|
|
|
|
|
|
|
|
|
= |
|
|
× |
|
|
|
w |
L1C1 |
|
= |
× |
|
|
|
|
w2 |
|
|
|
, где w2 |
= |
|
|
, w2 = |
|
. |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
1 |
|
|
|
2 |
|
|
|
|
wC2 |
- |
|
|
1 |
|
|
|
|
|
|
wC2 1- |
|
|
|
|
|
|
1 |
|
|
|
|
C2 1- |
w022 |
|
|
|
|
|
|
|
|
01 |
|
|
|
L1C1 |
|
|
02 |
|
|
L2C2 |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
wL2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
w |
L2C2 |
|
|
|
|
|
|
|
|
|
w2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
Z |
|
Z |
|
= R2 |
при условии, что w = w = w |
|
|
или L C |
|
= L C |
|
|
= |
1 |
. |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
01 |
|
|
|
02 |
0 |
|
|
|
|
|
|
1 1 |
|
|
2 |
|
2 |
|
w2 |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
В этом случае данный ЧП является полосовым фильтром типа «к», т.к. Z |
1 |
Z |
2 |
= R2 |
= k 2 . |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|||
|
|
Z |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
(w2 L2C2 -1)= |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
= j wL1 |
- |
|
|
|
|
|
|
|
|
× j wC2 - |
|
|
|
|
|
|
= -L1w 1 |
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Z 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
wC1 |
|
|
|
|
|
|
|
|
|
|
wL2 |
|
|
|
|
|
|
|
|
|
|
w |
L1C1 L2w |
|
|
|
|
|
|
|
- 2 + w02 |
|
|||||||||||||||||||||||||||||||||||||||||
|
= - L1 1- w02 |
|
× |
w2 |
-1 = - |
L1 w2 |
-1- w2 × w02 + w02 |
= - L1 w2 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
L2 |
|
|
|
w w0 |
|
|
|
|
|
|
|
|
|
|
|
L2 |
w0 |
|
|
|
|
w0 w w |
|
|
|
|
L2 |
w0 |
|
|
|
w |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
Z |
1 |
|
|
|
|
L |
|
|
w |
|
|
|
|
w |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Откуда |
|
|
|
|
|
= - |
|
1 |
|
|
|
|
|
|
|
- |
|
|
0 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
Z 2 |
|
|
|
|
L2 w0 |
|
|
|
|
w |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Из равенства следует, что Z1 |
|
и Z 2 |
разного знака. Это необходимо, чтобы ЧП был фильтром. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Определим граничные частоты полосы пропускания из условий: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z |
1 |
|
|
|
|
L |
|
|
|
f |
|
|
|
|
|
f |
0 |
|
2 |
|
|
Z |
1 |
|
|
|
L |
|
f |
|
|
f |
0 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
1 |
|
|
|
|
|
- |
|
|
|
|
|
= |
0 , |
|
|
|
= |
|
1 |
|
|
|
- |
|
|
|
|
|
|
|
= 1. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z 2 |
|
|
|
|
f0 |
|
|
f |
|
Z 2 |
|
|
|
|
f0 |
|
f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L2 |
|
|
|
|
|
|
|
|
|
|
|
|
L2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
После алгебраических преобразований: f |
= f0 , |
|
f |
- |
f0 |
= |
L2 |
, |
|
|
f |
- |
|||||||||||||
|
f0 |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
|
L1 |
|
f0 |
||||||
Из последних двух равенств определяем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
L |
|
|
L |
|
|
|
|
|
L |
|
|
|
||||||||||
|
|
f1 = f0 |
2 |
+1 - |
|
|
2 |
|
|
, |
f2 = |
f0 |
|
|
2 |
|
+1 + |
||||||||
|
|
|
|
|
4L |
|
|
4L |
|||||||||||||||||
|
|
|
4L |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|||||||
Видно, что f f |
2 |
= f 2 – центральная частота. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Две полосы пропускания в диапазоне частот: [ f1 , f0 ] |
и [ f0 , |
|
|
f2 ]. |
|
|
|
||||||||||||||||||
Две полосы задерживания в диапазоне частот: [0, |
f1 ) |
и ( f2 , ¥). |
|||||||||||||||||||||||
Построим частотные зависимости характеристических параметров: Частотные зависимости ослабления и фазы:
f0 |
= - |
L2 |
. |
|
|
||
f |
L1 |
||
L2 . 4L1
|
|
|
|
|
Ac |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Bc |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f0 |
|
|
|
f2 |
|
|
|
|
|
|
|
|
|
|
|
|
f |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
f1 f0 f2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
Частотные зависимости характеристических сопротивлений: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
f |
|
|
|
|
f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Z T = |
|
+ |
1 |
= R0 |
1- |
|
|
|
|
- |
|
0 |
, Z П = |
|
|
Z |
1 |
Z |
2 |
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Z1 Z |
2 1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Z |
|
|
L |
|
|
|
f |
|
|
|
|
f |
|
|
|
|
|
|
|
|
|
Z1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1+ Z 2 |
|
|
|
|
|
|
|
|
|
|
|
|
1- |
|
L1 |
|
|
f |
- |
|
|
f0 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L2 |
|
f0 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
ZT |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ZΠ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
R0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
f1 |
|
|
|
|
|
|
|
|
f0 |
|
|
|
|
|
|
|
|
|
f2 |
|
|
|
|
|
|
|
f |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
f1 |
|
|
|
|
f0 |
|
|
|
|
f2 |
|
|
|
|
|
|
|
|
|
|
|
f |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

Лекция 10
Заграждающие фильтры (ЗФ) типа «к». Частотные зависимости ослабления, характеристических сопротивлений.
Представим полузвено ЗФ типа «к».
|
|
|
|
|
L1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Z |
|
|
|
|
|
|
|
L2 Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Т |
C1 |
|
|
П |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
C2 |
|
Z |
|
= |
1 |
= |
|
1 |
|
. |
Z |
|
= jωL + |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
Y 1 |
|
jωC1 |
+ |
1 |
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
jωL1 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
фазы и
1
jωC2
.
Граничные частоты определяются из равенства: |
Z1 |
|
= |
|
|
|
|
1 |
|
|
|
. |
|
Z 2 |
|
L |
|
f |
|
− |
f |
|
2 |
||||
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
2 |
|
|
|
|
0 |
|
|
|
|
|
|
L1 |
|
|
f |
|
||||||
|
|
|
|
|
|
f0 |
|
|
|||||
Построим частотные зависимости характеристических параметров:
Z T = |
|
|
+ |
Z |
1 |
|
= R0 |
1− |
L |
|
f |
− |
f |
0 |
2 |
П = |
Z |
1 |
Z |
2 |
|
= |
|
|
|
R |
|
|
|
|
|
|
||
Z1 Z |
2 1 |
|
|
2 |
|
|
|
|
, Z |
|
|
|
|
|
|
0 |
|
|
|
|
|
. |
||||||||||||
|
|
|
|
|
|
|
|
Z1 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
Z 2 |
|
|
L1 |
f0 |
|
f |
|
|
|
1+ |
|
|
1− |
L |
|
f |
− |
f |
|
2 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z 2 |
|
|
2 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L1 |
f0 |
f |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Zс1=ZΤ
ПП ПЗ ПП
R0 







0 |
f1 |
f2 |
f |
Ac
0 f1 |
f0 |
f2 |
f |
Zс2=ZΠ |
|
|
|
R0 |
|
|
|
ПП |
ПЗ |
|
ПП |
0 |
f1 |
f2 |
f |
Bc |
|
|
|
π |
|
|
|
|
f0 |
f2 |
f |
0 |
f1 |
|
|
−π |
|
|
|
Производные фильтры типа «m»
Поставим задачу создания последовательно-производного фильтра так, чтобы его
собственное сопротивление ZTm |
равнялось собственному сопротивлению ZT фильтра типа «к». |
|||||||||||||||||
Кроме того, потребуем, чтобы Z1m = mZ1 . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
Z1 |
|
|
|
|
|
Z1m |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ZТ |
|
Z2 |
|
|
ZП |
|
|
ZТm |
|
|
ZПm |
|||||
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Z2m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Поскольку ZTm = ZT , то получаем уравнение вида:
|
|
+ |
Z |
1 |
|
= |
|
|
+ |
Z |
1m |
|
Z1 Z |
2 1 |
|
|
Z1m Z |
2m 1 |
|
||||||
Z 2 |
Z 2 m |
|||||||||||
|
|
|
|
|
|
|
|
|||||
После алгебраических преобразований получаем:
.

|
Z 2m |
= |
1- m2 |
|
Z1 |
+ |
1 |
|
Z |
2 . |
||||||
|
m |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
m |
|
|||||||
|
|
|
|
mZ1 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
1 |
|
Z2 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||||||
ZТm=ZТ |
m |
|
|
|
|
ZПm |
||||||||||
|
|
|
|
1-m2 |
Z1 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
m |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из последнего соотношения видно, что сопротивление Z 2m состоит из последовательного соединения двух сопротивлений: сопротивления того же знака, что и Z 2 , и сопротивления противоположного знака, как Z1 . При m = 1 фильтр типа «m» превращается в фильтр типа «к».
Отметим, что граничные частоты фильтра типа «m» и типа «к» совпадают. Действительно:
Z1m |
= |
|
|
mZ1 |
|
|
= |
m2 |
|
|
|
× |
Z 1 |
. |
|
|
|
- m2 |
|
|
|
|
|
|
Z |
|
|
||||
Z 2m 1 |
|
|
1 |
|
|
2 |
|
1 |
|
Z 2 |
|||||
|
|
|
|
Z1 |
+ |
|
Z 2 |
1+ (1- m |
) |
Z 2 |
|
|
|
||
|
|
|
m |
m |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
Выясним, чему равно собственное сопротивление последовательно-производного фильтра со стороны Пm-входа.
|
|
Z1m Z 2m |
|
|
|
Z1 Z 2 |
|
|
+ (1 |
- m2 ) |
Z1 |
|
|
+ (1- m2 ) |
Z1 |
|
|||||
ZПm = |
|
= |
|
|
1 |
|
= ZП 1 |
. |
|||||||||||||
|
|
|
|
||||||||||||||||||
1+ |
Z1m |
|
|
1+ |
Z1 |
|
|
|
|
|
Z 2 |
|
|
Z 2 |
|||||||
Z 2m |
Z 2 |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Параллельно-производный фильтр получается, если выполняются следующие требования:
|
|
|
|
|
|
|
|
|
|
ZПm = ZП , Z 2m |
= |
1 |
Z2 . |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
||||||
Согласно условию равенства характеристических сопротивлений: |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
Z1m |
Z 2m |
|
= |
|
|
Z1 Z 2 |
. |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
1+ |
Z1m |
|
|
|
|
|
|
1+ |
|
Z1 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
Z 2m |
|
|
|
Z 2 |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Подставляя значение Z 2m , получаем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
Z1m |
= |
|
mZ1 |
или |
1 |
+ |
m |
= |
1 |
|
|
+ |
|
|
1 |
|
|
|
, далее |
1 |
= |
1 |
+ |
1- m2 |
× |
1 |
|||||||||
|
|
|
mZ1m |
|
|
Z1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
1+ |
|
|
1+ |
|
Z1m |
|
|
Z 2 |
|
mZ1 |
|
mZ 2 |
Z1m |
|
mZ1 |
|
m Z 2 |
||||||||||||||||||||
|
Z 2 |
|
Z 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
mZ1
Z1
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ZТ |
|
Z2 |
|
|
ZП |
|
ZТm |
|
|
|
m |
|
|
|
|
|
|
|
ZПm=ZП |
|||||
|
|
|
|
|
|
|
|
|
Z2 |
|
|
|
|
||||||||||||
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
1-m |
2 |
|
|
1 |
Z2 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Определим собственное сопротивление параллельно-производного фильтра со стороны Тm-входа.
ZTm = |
|
|
+ |
Z |
1m |
|
= |
|
|
+ |
Z1 |
|
× |
1 |
|
= ZT |
1 |
|
|
|
|
Z1m Z |
2m 1 |
|
Z1 Z |
2 1 |
|
|
|
|
. |
||||||||||||
|
|
|
|
Z1 |
|
Z |
|
||||||||||||||
|
|
|
|
Z 2m |
|
|
|
|
Z 2 1+ (1- m2 ) |
|
1+ (1- m2 ) |
1 |
|
|
|||||||
|
|
|
|
|
|
Z 2 |
|
Z 2 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
