opevs

71

Из полученных выражений следует, что

максимальная абсолютная ошибка не превышает половины значения младшего разряда мантиссы с учетом порядка,

относительная точность представления чисел в форме с плавающей запятой почти не зависит от величины числа.

72

25. Кодирование двоичных чисел со знаком: прямой код.

При записи двоичных чисел со знаком в их формате необходимо предусмотреть два поля: поле, определяющее знак числа, и поле, характеризующее модуль числа. Под знак числа отводится специальный знаковый бит (двоичный разряд). Остальные разряды определяют модуль числа. Знаковый разряд приписывается слева от модуля числа, причём знаку "+" соответствует нулевое значение знакового бита, а знаку "-" - единичное.

Прямой код — способ представления двоичных чисел с фиксированной запятой в компьютерной арифметике. Главным образом используется для записи неотрицательных чисел.

При представлении в прямом коде числа со знаком, его старший разряд (старший бит) объявляется знаковым разрядом. Если его значение равно 0 — то число положительное, если 1 — то отрицательное. В остальных разрядах записывается двоичное представление модуля числа.

Представление чисел в прямом коде имеет существенный недостаток - формальное суммирование чисел с различающимися знаками даёт неверный результат.

Прямой код имеет ещё один недостаток - нуль имеет два различных

73

26. Кодирование двоичных чисел со знаком: дополнительный код.

При записи двоичных чисел со знаком в их формате необходимо предусмотреть два поля: поле, определяющее знак числа, и поле, характеризующее модуль числа. Под знак числа отводится специальный знаковый бит (двоичный разряд). Остальные разряды определяют модуль числа. Знаковый разряд приписывается слева от модуля числа, причём знаку "+" соответствует нулевое значение знакового бита, а знаку "-" - единичное.

Дополнительный код — наиболее распространённый способ представления отрицательных чисел в компьютерах. Он позволяет заменить операцию вычитания на операцию сложения и сделать операции сложения и вычитания одинаковыми для знаковых и беззнаковых чисел, чем упрощает архитектуру ЭВМ.

Преобразование числа из прямого кода в дополнительный осуществляется по следующему алгоритму:

1.Если число, записанное в прямом коде, положительное, то к нему дописывается старший (знаковый) разряд, равный 0, и на этом преобразование заканчивается;

2.Если число, записанное в прямом коде, отрицательное, то все разряды числа инвертируются, а к результату прибавляется 1. К получившемуся числу дописывается старший (знаковый) разряд, равный 1.

74

27. Кодирование двоичных чисел со знаком: обратный код.

При записи двоичных чисел со знаком в их формате необходимо предусмотреть два поля: поле, определяющее знак числа, и поле, характеризующее модуль числа. Под знак числа отводится специальный знаковый бит (двоичный разряд). Остальные разряды определяют модуль числа. Знаковый разряд приписывается слева от модуля числа, причём знаку "+" соответствует нулевое значение знакового бита, а знаку "-" - единичное.

Обратный код — один из способов кодирования отрицательных двоичных чисел. Он позволяет заменить операцию вычитания на операцию сложения.

Преобразование числа из прямого кода в обратный осуществляется по следующему алгоритму:

1.Если число, записанное в прямом коде, положительное, то к нему дописывается старший (знаковый) разряд, равный 0, и на этом преобразование заканчивается;

2.Если число, записанное в прямом коде, отрицательное, то все разряды числа инвертируются. К получившемуся числу дописывается старший (знаковый) разряд, равный 1.

Хотя обратный код и позволяет решить проблему сложения и вычитания чисел с различными знаками, он имеет и недостатки. Во-первых, процесс суммирования чисел является двухэтапным, что увеличивает время выполнения этой операции. Во-вторых, как и в прямом коде, в обратном - два представления нуля:

1)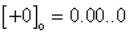 и .

2)

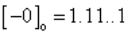
75

28. Сложение и вычитание двоичных чисел в форме с фиксированной запятой со знаком в прямых кодах. Особенности выполнения операций над числами без знака.

Поскольку организовать аппаратную реализацию сложения двух чисел значительно проще, чем вычитание, то в ВМ более широкое распространение получило приведение ариметических операций к двум основным операциям: сложению и сдвигу. Операция вычитания одного числа их другого сводится к сложению числа с отрицательным знаком.

Правила сложения чисел в прямом коде не отличаются от обычных правил сложения, т.е. если оба слагаемых имеют одинаковые знаки, то их числовые разряды складываются, а сумме приписывается знак одного из них. Если слагаемые разных знаков, то из числовых разрядов большего по абсолютной величине числа вычитается меньшее, а сумме приписывается знак большего слагаемого. При этом числовые разряды кода обрабатываются отдельно от знаковых, т.к. последние не имеют веса. При сложении в прямых кодах отсутствует цепь поразрядного переноса между старшим значащим и знаковым разрядами. Таким образом, в прямом коде знаковый разряд и цифровую часть нельзря рассматривать как единое целое. Он не применяется для выполнения операции алгебраического сложения, но он удобен при выполнении оперции умножения и деления.

Среди особенностей выполнения операций над числами без знака можно выделить вычетание. Если представить его как A-B=C, то обязательно должно быть A>=B. Так же особенностью является наличие перепонений. При сложении чисел в прямом коде признаком переполнения разрядной сетки является появление единицы переноса из старшего разряда значащей части числа. Так как переполнение возникает лишь при сложении чисел с одинаковыми знаками, то признаком переполнения при сложении чисел в дополнительном и обратном кодах может служить противоположность знака результата знакам слагаемых. В ЭВС для обнаружения переполнения анализируются переносы в знаковый разряд и из знакового разряда. Если эти переносы либо оба отсутствуют, либо оба имеются, то переполнения нет. Наличие переноса только в знаковый разряд либо только из знакового разряда является признаком того, что имеет место переполнение.

76

29 Сложение и вычитание двоичных чисел в форме с фиксированной запятой со знаком в дополнительных кодах

Сложение в дополнительных кодах характеризуется наличием цепи поразрядного переноса из старшего разряда значащей части в знаковый разряд.

Теорема: Сумма дополнительных кодов чисел есть дополнительный код суммы чисел.

При сложении чисел с использованием дополнительного кода выполняется арифметическое сложение кодов слагаемых, включая их знаковые разряды, с учетом возможного переноса в знаковый разряд из старшего значащего разряда суммы. При возникновении переноса из знакового разряда суммы единица переноса отбрасывается. При сложении код знака результата получается автоматически.

Пример:

Сложить два числа в дополнительных кодах: А=+1001, В=-101 (n=4).

Решение:

[A]доп=01001, [В]доп=11011 => 01001+11011=100100. Старший разряд – единица переноса из знакового разряда, которая отбрасывается. Следовательно,

A+B=00100=+100

Операция вычитания чисел в ЭВС сводится к операции сложения с использованием дополнительного и обратного кодов. Например: A-B=A+(-B).

77

30. Сложение и вычитание двоичных чисел в форме с фиксированной запятой со знаком в обратных кодах.

Сложение в обратных кодах характеризуется наличием цепи поразрядного переноса из старшего разряда значащей части в знаковый разряд, а так же цепи кругового или циклического, переноса из знакового разряда в младший разряд значащей части.

Теорема: Сумма обратных кодов чисел есть обратный код суммы чисел

При сложении чисел с использованием обратного кода выполняется арифметическое сложение кодов слагаемые, включая из знаковые разряды. При возникновении переноса из знакового разряда суммы единица переноса прибавляется к младшему разряду суммы. Такой перенос называется круговым или циклическим. При сложении код знака результата получается автоматически.

Пример:

Сложить два числа в обратных кодах: A=+1001, B=-1010 (n=4).

Решение:

[A]обр=01001, [B]обр=11010 => 01001+11010=100011. Старший разряд

циклически переносим в младший разряд суммы: 00011+1 = 00100 = +100.

Операция вычитания чисел в ЭВС сводится к операции сложения с использованием дополнительного и обратного кодов. См. пример выше A+(- B)=A-B.

78

31 Переполнение при сложении чисел с фиксированной запятой. Модифицированные коды

При сложении двух чисел с одинаковыми знаками может получиться результат, превосходящий по абсолютной величине максимально допустимое для данного формата число, т.е. для представления абсолютного значения результата потребуется n+1 двоичный разряд. Такой результат называют переполнением разрядной сетки.

При сложении правильных дробей переполнение означает, что результат по абсолютной величине получится большим или равным 1, а при сложении целых чисел – 2n.

Если при сложении чисел с фиксированной запятой происходит переполнение, то результат не может быть использован в дальнейших вычислениях. Случаи переполнения в ЭВМ фиксируются с помощью специального флага.

При сложении числе в прямом коде признаком переполнения разрядной сетки является появление единицы переноса из старшего разряда значащей части числа.

Т.к. переполнение возникает лишь при сложении чисел с одинаковыми знаками, то признаком переполнения при сложении чисел в дополнительном и обратном кодах может служить противоположность знака результата знакам слагаемых.

Чтобы обнаружить переполнение разрядной сетки можно ввести в знаковую часть изображения числа вспомогательный разряд, который называют разрядом переполнения.

Такое представление числа называется модифицированным, а коды – модифицированным прямым, дополнительным и обратным кодами.

С формальной точки зрения, модификация прямого, дополнительного и обратного кодов состоит в том, что для кодирования знака числа отводится не один, а два знаковых разряда.

Сложение чисел в модифицированных кодах сводится так же к их арифметическому сложению, при этом оба знаковых разряда участвуют в сложении наравне со значащими разрядами.

В дополнительном мод. коде единица переноса суммы теряется, а в обратном мод. – прибавляется к младшему разряду суммы.

Признаком переполнения при использовании модифицированных кодов является комбинация в знаковых разрядах суммы: 10 (при сложении отрицательных чисел), 01 (при сложении положительных чисел).

79

32. Умножение чисел с фиксированной запятой: общая схема целочисленного умножения

В общем случае вычисление произведения P(p2n-1p2n-2…p1p0) двух n- разрядных двоичных чисел без знака множимого (Мн) A(an-1an-2…a1a0) и множителя (Мт) B(bn-1bn-2…b1b0) сводится к формированию частных произведений (ЧП) Wi по одному на каждую цифру множителя, с последующим суммированием полученных ЧП.

Перед суммированием каждое частичное произведение должно быть сдвинуто на один разряд относительно предыдущего согласно весу цифры множителя, которой это ЧП соответствует.

Перемножение двух n-разрядных двоичных чисел P=AxB приводит к получению результата, содержащего 2n разрядов.

Поскольку сомножителями являются двоичные числа, вычисление ЧП упрощается – если цифра множителя bi, равна 0, то Wi тоже равно 0, а при bi=1 частичное произведение равно множимому Wi=A.

Алгоритм умножения предполагает последовательное выполнение двух операций – сложения и сдвига.

Суммирование ЧП обычно производится не на завершающем этапе, а по мере и получения. Это позволяет избежать необходимости хранения всех ЧП, то есть сокращает аппаратные затраты.

Процесс получения произведения включает умножение множимого A на каждый разряд bi множителя B. Получаемые при этом частичные произведения Wi=Abi последовательно складываются (накапливаются), образуя суммы частичных произведений (частичные суммы) СЧП. Последняя сумма частичных произведений равна полному произведению.

80

Такая последовательность называется циклом умножения. На каждом цикле умножения сначала определяется очередное ЧПi, далее ЧПi, прибавляется к СЧП в результате чего определяется очередная сумма частичных произведений СЧПi, и так до получения СЧПn, и так до получения СЧПn, которое и представляет собой полное произведение.

Для правильного накопления сумм частичных произведений в каждом цикле умножения множимое (очередное ЧП) должно сдвигаться:

Влево – при умножении с младших разрядов множителя.

Вправо – при умножении со старших разрядом множителя.

При этом сумма ЧП должна быть неподвижна.

Правильное накопление сумм ЧП будет происходить так же в случае, если множимое на каждом цикле умножения добавлять в одни и те же разряды, т.е. сделать его неподвижным, а после каждого очередного суммирования сдвигать очередную сумму частичных произведений

Вправо – при умножении с младших разрядов множителя.

Влево – при умножении со старших разрядов множителя.

Таким образом возможны 4 варианта реализации схемы умножения:

1.Умножение, начиная с младших разрядов множителя, при сдвиге множимого влево и неподвижной сумме ЧП

2.Умножение, начиная со старших разрядов множителя, при сдвиге

суммы частичных произведений влево и неподвижном множимом. Применив схему Горнера, выражение для произведения можно

записать следующим образом:

Выражения в скобках в формуле представляют собой последовательные значения СЧПi, определяемые рекуррентной формулой