
gotovaya_shpora
.docx|
Матрицы. Основные понятия. Действия над матрицами. Элементарные преобразования матриц. Матрицей наз прямоуг таблица чисел, содерж m-строк и n-столбцов. Матрицы равны между собой, если равны соответств элементы этих матриц. Матрица, в которой m=nназ квадратной или n-ого порядка. Квадр матрица, у которой все элементы, кроме элементов гл диагонали, равны 0 еаз диагональной. Диаг матрица, у которой каждый элемент главной диаг =1 наз единичной. Квадратная матрица наз треуг, если все элементы, расположенные по одну сторону её гл диаг =0. Матрица, у которой все числа, стоящие на гл диаг не нулевые, а также некоторое кол ненулевых строк, наз трапециевидной. Матрица, содерж один столбец или строку, наз вектором из Rn пр-ва. Действия. Сложение – только для матриц одинакового размера. Умножение на число. Множества матриц одинакового размера обознач Mm*n. Тогда введённое на этом мн-ве операции сложения и умнож на число превращ Mm*n в линейное пр-во, векторами которого явл матрицы m*n. Умножение на вектор-столбец. Для умножения матрицы на вектор-столбец надо, чтобы число столбцов матрицы было равно числу координат вектора. Две матрицы наз эквивалентными, если одна из них получена из другой с помощью эл. Преобраз. Любую матрицу можно привести к канонической.
Определители n-го порядка. Свойства. Теорема о разложении определителя n-го порядка по элементам ряда. Основные методы вычисления определителей n-го порядка. С помощью опред 4-ого порядка можно посчитать опред n-ого порядка. Для опред любых порядков остаются в силе определение минора и алг доп некоторого элемента, а также 2-теоремы об алг доп. Обозначим Mik –минор для элемента Аik и для определителя n-ого порядка: Aik=(-1)i+kMik. Пусть D-опред n-ого порядка. Раскрывая его сначала по элементам i-той строки, а затем по – k-ого столбца в силу теоремы1 получим D=ai1Ai1+…ainAin. D=a1kA1k+…ankAnk. C другой стороны, если i не=j и kне=l, то D=ai1A1i+…+ajnAni=0; D=a1kA1l+…ankAnl=0. Теорема: сумма все произведений элементов любой строки определителя на соотв алг доп равна этому определителю. Замечание: определитель треуг матрицы А равен произ элементов, стоящих на диагонали. Теорема: опред произ 2х матриц одинакового порядка=произв опред n-ого порядка. Теорема: опред матрицы порядка n равен сумме произ всевозможн миноров k-ого порядка (k<n), которые можно получить из произв выбранных k-направелнных рядов и алг. доп этих миноров.
Невырожденные матрицы. Обратная матрица. Методы вычисления обратной матрицы. Пусть матрица A квадратная n-ого порядка. Квадратная матрица наз невырожденной, есил её определитель отличен от 0, в противном случае матрицы вырожденные. Матрица нах присоединённой к матрице А, если она имеет вид (см рис) , где Aij – алг доп элемента aij и данной матрице А.Матрица A-1 – обратная матрица А, если A-1*A=A*A-1=E, где E –единичная матрица. A-1 имеет те же размеры, что и A. Теорема: всякая невырожденная матрица имеет обратную. Св-во: 1) det(A-1)=1/detA; 2)(A*B)-1=B-1*A-1; (A-1)T=(AT)-1. Методы: 1)метод присоединённой матрицы (союзная – A*). А*-опред как транспонированная матрица, составл из алг доп соотв элементов матрицы А. 2)Для данной матрицы An-ого порядка построим прямоуг матрицу ГА=(А/Е) размером n*2n, приписывая к А справа единичную матрицу используя элементарные преобраз над строками приводим ГА к виду ГА=(Е/В), что всегда возможно при A невырожденоой. =>B=A-1, т.е. (А/Е)=(Е/A-1).
ЛП. Определение. Свойства. Примеры. Множества векторов V, в котором определены внутренние операции сложения и внешние операции умножения на число, и если эти операции удовлетворяют аксиомам, то множество наз лин пространством. Аксиомы (x,y,z€V) 1)x+y=y+x 2)(x+y)+z=x+(y+z) 3)x+0=x 4)x+(-x)=0 5)1*x=x 6)α(βx)=(αβ)x 7)α(x+y)=αx+αy 8)(α+β)x=αx+βx; свойства(х вектор!!!):1) в лп сущ ед нулевой вектор 2)в лп для каждого х сущ ед противоположный –х. 3)-х противоположным явл х. 4)Произведение числа х на 0 есть нулевой вектор 5)-1*(х)=-х 6)α*Ō=Ō 7)если α*х=0 при αне=0 =>x=0; если α*х=Ō хне=0 =>α=0
Вопрос 2 Линейная зависимость(независимость) векторов. Основные теоремы. Если все Alii=1,n след. Комбинация наз. Тривиальной. Если хотябч один из коэф. Отлич. От 0 то-нетривиал. Сист. Векторов наз лин независимой если равентсво Al1*X1(вектор)+…ALn*Xn(вектор)=0 имеет место когда все Aln =0. Сист векторов наз линейно зависим. Если (это же равенсво) имеет место когда хотябы одно из чисел Xn не =0. Свойств: 1) X1..Xn (1) если среди веткоров нулевой вектор то они линейно зависимы..2) если (1) имеется К(K<n) лин зависимых векторов то (1)лин зависим. 3) если(1) лин независим то и люб часть етих векторов лин незава. 4) ЕСЛИ В СИСТ K –зависимых векторов присоед.любые n вектов то получи мсистему K+n линейно зависим векторов Теорема: для того чтобы(1)были лин незав. Необход и дост чтоб ни один из етих векторо не явл лин коомбин других векторов.
Вопрос 3 Размерность и базис ЛП. Матрица перехода от одного базиса к другому. Пусть ЛП V выполняется след. 1) сущn лин незав вектров 2) любая сист из n векторов лин зависима тогда число n-размервость ЛП V 3) пространтва размерность n наз n-мерным.. базис n-мерным простравсва V наз любая упорядочена сист n-линейно независим векторов етого пространсва.. e1…en – векторы образ базис. Тогда из векторов етого пространсва может представлен в виде лин комбин базисных векторов x=AL1e1+…ALnen (x,e-векторы ), Al1…ALn-коорд вектора X базиса е1..en. базис в пространстве не единственный. Теорема: если e1..en базис n-мерного пространсва то любой вектор X линейно выражается через e1..en однозначный образом. Теорема2: если e1..enn-линейно независим векторв пространства Vn и любой вектор x из Vn явл лин комбин етих векторов то e1..en базис n-мерного пространсва размерностью n
|
Линейная зависимость строк в матрице. Ранг матрицы. Теорема о базисном миноре. Методы нахождения ранга матриц. Строки матрицы наз лин завис, если линейно зависимы векторы Ui из пространства Rn, Ui€Rn. Линейная зависимость системы вектором означает, что один из них есть линейная комбинация остальных векторов системы. Для матрицы А лин завис строк равносильна тому, что её некоторая строка явл линейной комбинацией остальных строк. Теорема: для всякой матрицы число её линейнозавис строк=числу линейнозавис столбцов. Ранг. Опред: максимальное число линейнозавис строк матрицы Aназ рангом матрицы и обознач r(a). Опред: наиб из порядков миноров данной матрицы отличных от 0 наз рангом матрицы. Св-ва: 1)при транспонировании rang=const. 2)если вычеркнуть нулевой ряд, то rang=const; 3)rang=cost, при элементарных преобразованиях. 3)для вычисл ранга с помощью элементар преобраз матрица A преобраз в матриц B, ранг которой легко находится. 4)ранг треуг матрицы=числу ненулевых элем, располож на глав. Диагоналях. Замечания: 1)rang канонич матрицы=числу единиц, стоящих на главной диагонали. 2)для квадратной матрицы n-ого порядка rangA=n, если матрица невыражд. Теорема: чтобы определитель n-ого порядка =0, надо чтобы строки(столбцы) были линейно зависимы. Следствия: 1)чтобы опред n-ого порядка=0 надо чтобы rangA<n; 2)чтобы опред n-ого порядка не =0 надо чтобы строки и столбцы были лин независ, т.е. rang=n; 3)чтобы векторы Un=(a11,a12…a1n)…Un=(an1,an2…ann) были лин завис надо чтобы определитель матрицы, строками с столбцами которой служ эти векторы, =0. Опред: базисными строками (столбцами) матрицы наз её любые R-независимых строк, где R –rang матрицы. Эти строки и стобцы наз базисными. Элементы матрицы, стоящие на пересеч фикс k-строк и k-столбцов образ квадр матрицу порядка K. Её определитель наз минором k-ого порядка (базисным). Теорема: для того чтобы ранг матрицы был равен R необходимо чтобы существовал не =0 минор порядка R, а минор (R+1)-ого порядка был =0. Методы. 1)с помощью преобразований любую матрицу можно преобраз к виду, когда каждый из её рядов будет состоять только из 0-ей или из 0-ей и единицы. Тогда число оставшихся единиц опр ранд. 2)Минор Мk+1-ого порядка, содерж в себе минор порядка k, наз окаймляющий минор Мк. Если у матрицы А сущ минор Мk не =0, а все окаймляющие=0, то rangA=K. Решение СЛАУ. Правило Крамера. Матричный метод. Система уравнений наз совместной, если имеет хотя бы одно решение, иначе она несовместна. Совместная система наз определённой, если она имеет единственное решение. Опред: системы наз равносильными, если они имеют одно и то же решение. Опред: cистема лин алг уравнений наз однородной, если все свободные члены=0. Пусть дана система n-лин ур с n неизвестными A*X=B. Если опред системы не=0, то система невыражденная. Надём решение при условии, что опред не=0. Умножим обе части ур-ия слева на матрицу A-1 и получим: X=A-1*B– это есть матричный способ реш СУ. Формула Крамера xi=∆i/∆, i=[1,n](∆-основной, ∆i-вспомогательный)Док: A*X=B, если detA не=0 =>сущ !A^(-1); X=A-1*B=1/detA*C *B))… Вывод: невырожденная система n-линейных ур-ий с n-неизвестными имеет единственное решение, которое находится матричным способом (1), либо по формуле Крамера.
Линейные
операторы. Матрицы линейного оператора.
Собственные числа и собственные
векторы линейного оператора. Пусть
V
и W
–два лин пр-ва. Оператором f?
действующим из V
в Wназ
отображение вида: f:V->W
или y=f(x).
При этом вектор y-наз
образом вектора x.
Оператор fназ
линейным, если вып: 1)f(x1+x2)=
f(x1)+f(x2);
2)f(λx)=
λf(x),
|
Системы линейных уравнений. Основные понятия. Теорема Кронекера-Капелли. Решение произвольной системы линейных уравнений.. Решением системы назn значений неизвестных x1=c1 … xn=cn, при подстановке которых все ур-ия системы обращаются в верное равенство. Опред: система уравнений наз совместной, если имеет хотя бы одно решение, иначе она несовместна. Совместная система наз определённой, если она имеет единственное решение. Опред: системы наз равносильными, если они имеют одно и то же решение. Замечание: эквивалентные системы получаются при элементарных преобразованиях при условии, что преобраз вып только под строками. Опред: cистема лин алг уравнений наз однородной, если все свободные члены=0. Теорема К-К: система лин алг ур-ий совместна, когда rangA=rangA с крышечкой.доказ:пусть система совместн.докажем что rangA=rangAA.. т.к система совместн. То сущ. С1бс2бСт которое обращает ур.системы. в ветное тождества с1a1+c2a2…cnan=B Где B-столбец свободных член.
Явл. Линейной комбинацией первых ее n столбцов. Вычитая из последнего столбца B получаем нулевой Столбец следоват. rangA1=rangA(черточка)=rangA Пусть rangA=rangA(черт) на основ.Т.о базисном миноре любой ряд матрицы явл. Лин.комбинац. параллельных emy базисных рядом. Послед. Столбец А(черт) явл. Лин. Комбинац. R базисных столбцов следовател. Всех столбцов матрицы A
Решение произвольных лау.. Осн теоремыТеорема Кронекера-Копелли: система лин алг ур-ий совместна, когда rangA=rangA с крышечкой. Теорема: если rang совместной системы= числу неизвестных, то система имеет одно решение. Теорема: если ранг совмест сист < числа неизвестных, то система имеет бесконеч решений. Правило решения СУ. 1)найти ранг основной и расширенной матрицы (если rA не =rA с крыш, то система несовместна. 2) если rA=rA с крыш и =r, то система совместна и надо найти базисный минор порядка r. 3)Берём r ур-ий из коэф которых составлен базисн минор. Остальные ур-ия отбрасываем. Неизвестные, коэф которых входят в минор наз главными. Из оставл слева, а остальные (n-r) – справа. 4)Найти выражения главных неизв через свободные. Получено общее решение системы 5)Придавая свободным низвестным произвольное значение, получим соотв значения главн неизв, т.е. найдём частные решения
Вопрос 4 Скалярное произведение векторов. Свойства. Вычисление. Приложение. Скалярным произв векторов наз число = произвед длин на косинус между ними. СПВ равно сумме произ их соотв координат. Скалярное произ 2х векторов = модулю одного умноженного на проекцию другого на соноправленную с 1-ым вектором ось. Св-ва: a*b=b*a; (C*a)*b=C*(a*b); a(b+c)=a*c+b*c; 2)(a)0.5=|a|; 5)aперпенлbиaне =0, bне=0, то |a|*|b|=0. Приложения. Cosσ=(a*b)/(|a|*|b|). Замечание: условие перпендикулярности двух ненулевых векторов: a перп baxbx+ayby+azbz=0. Проекция вектора: прba=(a*b)/|b|.
Вопрос 5 Векторное произведение векторов. Свойства. Вычисление. Приложение. Три некомпланарных вектора a, b, с взяты в указанном порядке и образуют правую тройку, если с конца 3-его вектора с кратчайший поворот от 1-ого a ко 2-ому b видим совершающийся против часовой стрелки, и левую – если по часовой. Опред: векторным произвед вектора a на bназc, который имеет длину, численно равную |c|=|a|*|b|*sinσ; и этот вектор ортогонален векторам a и b,векторы a, b, с образ правую тройку. Пункты: 1)условие коллиниарности: a||b =>[a*b]=0; 2)нахождение S параллелограмма и S треуг. Sпар=|a|*|b|*sinσ. Sтр=0,5*|a*b|. ;[a,b]=определитель |I,j,k:x,y,z(a);x,y,z(b)|
Вопрос 6 Смешанное произведение векторов. Свойства. Вычисление. Приложение. СПВ (a,b,c) наз число полученное след образом: (a,b,c)=([a,b],c). Смешанное произведение 3х векторов равно объёму параллелепипеда, построенного на этих векторах, взятого со знаком + (-), если эти векторы образуют правую (левую) тройку. Смешанное произ векторов равно определителю 3-его порядка, составленного из координа перемноженных векторов. Приложение. 1)определение взаимных ориентаций векторов в пр-ве: если abc>0 (abc<0), то правая (левая) тройка векторов abc. 2) abc компланарны(лежат в одной пл-ти), когда их произв =0. 3)Геометр смысл: Vпараллелепипеда= abc. Vтр=1/6(abc).
|
Системы однородных линейных уравнений. Нормированная фундаментальная система решений. Однородная система лин ур в матричн форме имеет вид A*X=0, где A- основная матрица системы (x1,…,xn)T €R. Однород сист всегда совместна. Теорема: для того чтобы однородая система имела не нулевое решена надо, чтобы rangA<n, где n-число её столбцов или неизвестных. Следствие: 1)чтобы однородная система n*n имела не нулевое решение надо, чтобы определитель матрицы |A|=0, т.е. когда r(A)<n. 2)чтобы однородная система n*n имела одно ненулевое решение, надо, чтобы r(a)=n или |A| не=0; Теорема: множество решений однородной системы образует подпространство лин пространства Rn, размерность которого =(n-r(A)). Пусть r(A)<n. Если число решений = размерности пространства решений, то их можно брать в качестве базиса этого пространства. Совокупность (n-r) лин нез решений однород системы наз фундаментальной системой решений. => всякий вектор решения X есть лин комбинация векторов E обознач X=Сумма от 1 до n-1 CiEi, где Ci- постоянная, а Ei –лин независ сист реш. (1) Решение X (1) наз общим решением лин однор систем a*x=0.
|
|
|
. Производная функции в точке. Механический и геометрический смысл производной. Опред: производной функции y=f(x) в произвольной точке x0наз предел отношения приращения функции к приращению аргумента при условии, что последнее ->0: y’(x0)=lim при ∆x->0 (f(x0+∆x)-f(x0))/∆x. Из св-ва пределов следует, что если функция f, определённая в некоторой окрестности в x0 имеет конечную производную F’(x0), то сущ производная слева и справа: F’(x0)=F’(x0-0)=F’(x0+0). Мех смысл. Производная – это мат модель скорости процесса, описываемого функцией. Если аргумент x0 функции получает приращение ∆x, что x0+∆x с той же окрестностью т. x0, то соответствующее приращение ∆f(x0)=f(x0+∆x)-f(x0). Средняя скорость <Vср>=∆f(x0)/∆x. Мгновенная скорость Vмг=lim при ∆x->0 ∆f(x0)/∆x=F’(x0). Скорости протекания процессов: 1)Мгновенная скорость движения мат точки М в момент времени t0 есть предел пути по времени: V=lim при ∆t->0 (S(t0+∆t)-S(t0)/∆t; 2)Мгновенное ускорение мат точки в фиксир момент времени есть V’: a=lim при ∆t->0 (V(t0+∆t)-V(t0)/∆t; 3) теплоёмкость тела – производная от Q/T: C=dQ/dT; 4) линейная плотность неоднородного тонкого стержня в x0: p(x0)=dm/dx; 5)мгновенное значение электродвижущей силы – индукции=скорости изменения магн потока: E=dФ/dt; 6)сила тока в контуре в момент времени t равна произ заряда по времени: I=dq/dt. Геометр. Производная y’ функции y(x) представляет собой tg угла наклона к графику функции; Ур-ние касательной к прямой: y-y0=F’(x0)(x-x0). Теорема о непрерывности дифференцируемой функции. Основные правила дифференцирования функций. Производные основных элементарных функций. Опред: функция y=f(x) наз диф в x0, если её приращение в этой точке может быть представлено в виде A∆x+0(∆x), где A€R; O(∆x) –беск мал функц более высокого порядка малости, чем ∆ч при ∆x->0. Таким образом дифференциальность функции в точке x0 означает, что с точностью до беск малой более высокого порядка, чем приращ ∆x приращ функции придставимо лин функц ∆x. Теорема: для того, чтобы функция f(x) в x0 была диф надо, чтобы в x0сущ конечная производная. Теорема: если функция f(x) диф в точке, то она непрерывна в этой точке. Если y=f(x) диф в точке x0€[a;b], то говорят, что она диф на отрезке ab. Пусть U(x) и V(x) имеют производные в x0 и в некоторой её окрестности, тогда основные правила диф: 1)(CU)’=CU’; 2) (U/C)’=1/C*U’; 3)(U+V)’=U’+V’; 4)(U*V)’=U’V+V’U; 5)(U/V)’=(U’V-V’U)/V2. Производные основных элем функций: 1)(xα)’=α*xα-1, α€R; 2)(ax)’=ax*lna; 3)(shx)'=chx; 4) (chx)’=shx; 5)(thx)’=1/ch2x; 6) (cthx)’=-1/sh2x.
|
Производная сложной, обратной, заданной параметрически функций. Если y=f(u), а u зависит от произвольного аргумента x, то y’=F’(u)*u’(x); (un)’=n*un-1*u’. Если для y=f(x) сущx=F’(y) причём в точке ч производная функция y=f(x) не =0, то для производной обратной функции соотв. точки y справедливо: (F-1(y))’=1/F’(x) или dy/dx=(1/dx)/dy. 51. Логарифмическое дифференцирование. Производная функции, заданной неявно. Заключается в том, что сначала логариф. данную функцию, а потом диф. Производную от логарифма y=f(x), которая >0 и имеет производную x€Xназ её логарифмической производной в точке x и равняется: (ln(f(x)))’=F’(x)/f(x) или lny=y’/y. Используем при нахожд показат функции виды y=u(x)v(x), а также, если функц содержит операции умнож, деление, в степень, корень. Диф неявных функций. Пусть ур-ие F задает y, как неявную функцию x. Дифференц. его по x считается, что y есть функция от x. Получаем ур-ие, содерж x,y,y’. Выражая из него y’ находим произв. Функции y=f(x), котор задана в неявном виде. Диффер функции задан параметрически. Пусть y=y(x) задана параметрически x=γ(t) и y=φ(t), где t€T, тогда производная равна: y’(x)= φ’(t)/ γ’(t), x=γ(t) =>dy/dx=y’(t)/x’(t), x=γ(t)/ Воспользуемся для x=acost и y=bsint и получим y’(x)=bcost/-asint=-b/a*ctgt, x=acost. Дифференциал функции. Инвариантность формы дифференциала. Приближенные вычисления с помощью дифференциала. Опред: если приращ функции y=f(x) в т. x€X может быть представлено в виде A∆x+0(∆x), то главная часть этого приращения линейно относительно ∆xназ дифференциал функции y=f(x) в т. x и dy=A∆x. dy=F’(x)* ∆x т.к. dx=x, то dx=∆x и тогда dy=F’(x)dx. Отсюда следует, что задача нахожд. Диф. функции f(x) равносильна нахожд её производной. Формулы: 1) d(CU)=CdU; 2) d(U+/-V)=dU+/-dV; 3) d(V*U)=VdU+UdV; 4) d(U/V)=(VdU-UdV)/V2, V не =0. Геометр. Интерпритация диф функции. Из определения ∆f(x0)=df(x0)+Ө(∆x), т.е. диффер функции в x0 отличается от соотв приращения функции на бесконеч малую величину более высокого порядка малости, чем ∆x->0. т.к. F’(x)=tgα, то диф функции измер отрезком, т.е. dy функции y=f(x) в x0 изображается приращением ординаты в точке касательной, проведённой касательной к М с корд М(x;f(x0)) и линии y=f(x). Применение диф в приближ вычислениях. ∆y=dy; f(x0+∆x)=f(x0)+F’(x0)*∆x. Инвариантность. Диф функции равен произв функции на дифференц аргумента независимо явл ли этот аргумент независ переменной или функц независ перемен. Форма дифференц може быть сохр тогда, если преждняя независ переменная заменена 1-ой.
|
Производные и дифференциалы высших порядков. Производные высших порядков от функций, заданных неявно, параметрически. Производной 2-ого порядка y=f(x) наз произв от её производной y’=F’(x). Обозначается F’’(x) или d2y/dx2. Для нахожд. второй производной на уже найденную 1-ой функцию надо найденную 1-ую продиф по x, считая y-функцией от x. В выражении второй произ войдут x,y,y’. Подставляя вместо y’ её значения находим y’’, которое будет зависеть от x и y. Аналогично для др. порядков. x=k(t), y=p(t) =>y’x=y’t/x’t, x=k(t) =>y’x=(y’x)’t/x’t=k(t) =>y’x=(y’x)’t/x’t=(y’tx’t-y’tx’’t)/((xt)2x’t)=(y’’tx’t-y’tx’’t)/(x’t)3 =>d2y/dx2, x=k(t) =>x=t2+2t, y=ln(t-1). Опред: диф от диф y=f(x) в точке x наз. 2-ым диф. в т. x и обознач d2y или d(dy) В слачае, когда x-независ переменная, то для диф n-ого порядка справедливо: dny=F’’(x)*(dx)n. 54.
Теоремы о среднем значении. Теорема
Ролля. Пусть
f(x)
удовл. след условиям на [a;b]:
f(x)
определена и непрерывна на [a;b],
диф на (a;b)
и f(a)=f(b)
– тогда сущ хотя бы одна точка N€(a;b)
такая, что f(N)=0.
Док-во: если f(x)-непрерывна
на [a;b],
то на нём f(x)
принимает наиб и наим знач: 1) если M=m
=>f(x)=const
=>F’(x)=0;
2) если M>m
=> хотя бы одно из 2-х знач. M
и m
функция принимает в некот точке N€[a;b]
на основе f(a)=f(b).
Пусть f(N)=m
=>f(x)≥f(N).
Покажем, что F’(N)=0,
тогда согласно условию 2 для f(x)
сущ конечная производная F’(N)€(a;b).
Для Теоремы о среднем значении. Теорема Лагранжа. Если f(x) непрерывна на [a;b] и диф на (a;b), то сущ точка N€(a;b) и f(b)-f(a)=F’(N)(b-a) (1). Док-во: 1) составим вспомогат функицию p(x)=(b-a)*f(x)-(f(b)-f(a))x; 2) покажем, что p(x) удовл. теореме Роля: p(x) –непрерывна на [a;b], диф на (a;b) и p(a)=b*f(a)-a*f(b); 3) F’(x)=(b-a)*p’(x)-(f(b)-f(a)). Поэтому сущ точка N€(a;b), что p’(N)=0, т.е. (b-a)F’(N)-(f(b)-f(a))=0 =>f(b)-f(a)=F’(N)*(b-a). Теор Лагранджа наз теор о конечных преращениях – F’(N)=(f(b)-f(a))/(b-a), N€(a;b). Геометр смысл. (f(b)-f(a))/(b-a)=k –угловой коэф. хорды AB, af’(N) –угл. коэф. касательной к f(x) в т.С. Поэтому имеем, что между A и B на дуге AB найдётся т. С, в которой касательная // хорде AB при условии, что в каждой точке дуги ФИ сущ. касательная. Если положить, что f(a)=f(b), то получим теорему Роля. Положим в (1) a=x0, b=x0+∆x, тогда f(x0+∆x)*f(x0)=F’(N)∆x. и x0≤N≤x0+∆x.
|
56.
Теоремы о среднем значении. Теорема
Коши. Пусть
f(x)
и g(x)
удовл. след.условию: 1)непрерывны на
[a;b];
2) диф. на (a;b)
и g’(x)не
=0, .
Правило Лопиталя-Бернулли. Методы
раскрытия неопределенностей вида
0*∞, 00,
∞0,
1∞.
Теорема:
если функции f(x)
и g(x)
удовл. след условиям: 1) определены и
диф на (a;b)
за исключением x0
и g(x)не
=0; g’(x)не
=0ж
|
Формула
Тейлора. Разложение по формуле Маклорена
функций ех,
sinx,
cosx,
ln(1+x),
(1+x)m.
Всякий
многочлен в степени n:
Pn(x)=a0+a1x+a2x2+…+anxn,
(an
не=0) можно записать по степеням (x-x0)
пользуясь: Pn(x)=
Pn(x0)+
Pn‘(x0)/1*(x-x0)+Pn"(x0)/2!*(x-x0)2+…+Pn‘n(x0)/n!*
(x-x0)n
– формула Тейлора. Если f(x)
диф (n+1) раз в некоторой z-окрестности
точки x0,
то для F(x)=ex и F(0)=1; … Fn(x)=ex и Fn(0)=1; Fn+1(x)=ex и Fn+1(Өx)=eӨx=>ex=1+x+x2/2!+…+xn/n!+ Rn(x) где Rn(x)=xn+1/(n+1)!*eӨx, где Ө€(0;1) F(x)=sinx и F(0)=0; F’(x)=sin(x+П/2) и F’(0)=1;… Fn(x)=sin(x+n*П/2) и Fn(0)=sin(n*П/2) =>sin(x)=x-x3/3!+x5/51-…+xn/n!*sin(n*П/2)+ Rn(x) где Rn(x)= xn+1/(n+1)!*sin(Өx+(n+1)*П/2), где Ө€(0;1) cosx=1-x2/2!+x4/4!-…+xn/n!*cos(n*П/2)+ Rn(x), где Rn(x)= xn+1/(n+1)!*cos(Өx+(n+1)*П/2), где Ө€(0;1) ln(1+x)=x-x2/2+x3/3-…+(-1)n+1*xn/n+Rn(x), где Rn(x)= (-1)n+1*xn+1/((n+1)*(1+Өx)n+1), где Ө€(0;1) (1+x)m=1+mx+m(m-1)/2!*x2+…+((m-1)m…(m-n+1))/n!*xn+Rn(x), где Rn(x)=(m(m-1)…(m-n))/(n+1)!*(1+Өx)m-n-1*xn+1 где Ө€(0;1)
|

 b
b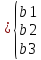 последнй столбец А(с черточкой
последнй столбец А(с черточкой