ТР 10 - одномерная выборка колупанович
.docxЗадание №10.
Одномерная выборка
Получим вариационный ряд из исходного:
|
-1,23 |
-1,07 |
-1,06 |
-1,05 |
-0,92 |
-0,9 |
-0,88 |
|
-0,67 |
-0,67 |
-0,58 |
-0,25 |
0,08 |
0,23 |
0,25 |
|
0,31 |
0,43 |
0,57 |
0,75 |
0,84 |
1,18 |
1,23 |
|
1,24 |
1,48 |
1,56 |
1,56 |
1,77 |
1,78 |
2,38 |
|
2,65 |
3,21 |
3,62 |
3,67 |
3,76 |
3,9 |
3,92 |
|
3,99 |
4,07 |
4,08 |
4,11 |
4,32 |
4,35 |
4,45 |
|
4,6 |
4,66 |
5,07 |
5,26 |
5,64 |
5,7 |
5,9 |
Сделаем таблицу для построения графика эмпирической функции F*(x), которая определяется формулой:
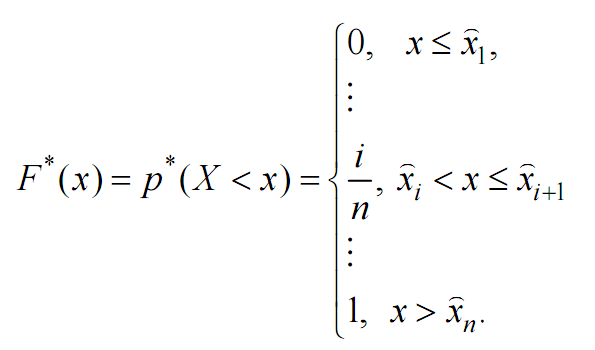
При этом исключим повторяющиеся значения.
|
m |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
x |
-1,23 |
-1,07 |
-1,06 |
-1,05 |
-0,92 |
-0,9 |
-0,88 |
-0,67 |
|
F*(x) |
0,020408 |
0,040816 |
0,061224 |
0,081633 |
0,102041 |
0,122449 |
0,142857 |
0,163265 |
|
|
|
|
|
|
|
|
|
|
|
m |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
|
x |
-0,58 |
-0,25 |
0,08 |
0,23 |
0,25 |
0,31 |
0,43 |
0,57 |
|
F*(x) |
0,204082 |
0,22449 |
0,244898 |
0,265306 |
0,285714 |
0,306122 |
0,326531 |
0,346939 |
|
|
|
|
|
|
|
|
|
|
|
m |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
|
x |
0,75 |
0,84 |
1,18 |
1,23 |
1,24 |
1,48 |
1,56 |
1,77 |
|
F*(x) |
0,367347 |
0,387755 |
0,408163 |
0,428571 |
0,44898 |
0,469388 |
0,489796 |
0,530612 |
|
|
|
|
|
|
|
|
|
|
|
m |
25 |
26 |
27 |
28 |
29 |
30 |
31 |
32 |
|
x |
1,78 |
2,38 |
2,65 |
3,21 |
3,62 |
3,67 |
3,76 |
3,9 |
|
F*(x) |
0,55102 |
0,571429 |
0,591837 |
0,612245 |
0,632653 |
0,653061 |
0,673469 |
0,693878 |
|
|
|
|
|
|
|
|
|
|
|
m |
33 |
34 |
35 |
36 |
37 |
38 |
39 |
40 |
|
x |
3,92 |
3,99 |
4,07 |
4,08 |
4,11 |
4,32 |
4,35 |
4,45 |
|
F*(x) |
0,714286 |
0,734694 |
0,755102 |
0,77551 |
0,795918 |
0,816327 |
0,836735 |
0,857143 |
|
|
|
|
|
|
|
|
|
|
|
m |
41 |
42 |
43 |
44 |
45 |
46 |
47 |
|
|
x |
4,6 |
4,66 |
5,07 |
5,26 |
5,64 |
5,7 |
5,9 |
|
|
F*(x) |
0,877551 |
0,897959 |
0,918367 |
0,938776 |
0,959184 |
0,979592 |
1 |
|
m – номер числа в вариационном ряду.
График эмпирической функции, совмещённый с графиком гипотетической функции, представлен в конце задания на миллиметровой бумаге.
Определим количество непересекающихся и примыкающих друг к другу интервалов:
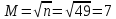
Построим гистограмму равноинтервальным методом. Определим длину интервала:
|
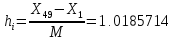
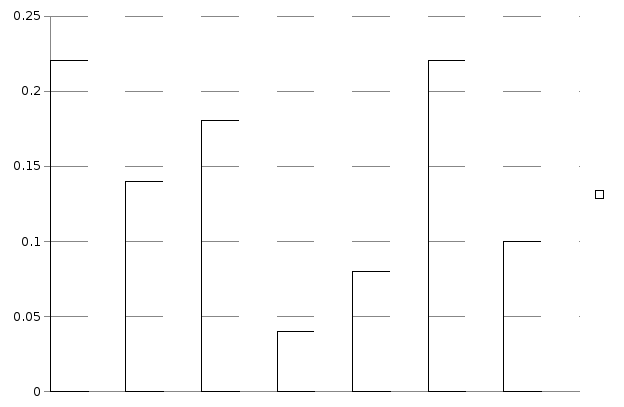
i |
Ai |
Bi |
hi |
vi |
Pi* |
fi* |
|
1 |
-1,23 |
-0,21 |
1,0185714 |
11 |
0,22449 |
0,220397 |
|
2 |
-0,21 |
0,81 |
1,0185714 |
7 |
0,142857 |
0,140252 |
|
3 |
0,81 |
1,83 |
1,0185714 |
9 |
0,183673 |
0,180325 |
|
4 |
1,83 |
2,84 |
1,0185714 |
2 |
0,040816 |
0,040072 |
|
5 |
2,84 |
3,86 |
1,0185714 |
4 |
0,081633 |
0,080144 |
|
6 |
3,86 |
4,88 |
1,0185714 |
11 |
0,22449 |
0,220397 |
|
7 |
4,88 |
5,90 |
1,0185714 |
5 |
0,102041 |
0,10018 |
Построим гистограмму равновероятностным методом.
|
i |
Ai |
Bi |
hi |
vi |
Pi* |
fi* |
|
1 |
-1,23 |
-0,775 |
0,455 |
7 |
0,142857 |
0,313972 |
|
2 |
-0,775 |
0,28 |
1,055 |
7 |
0,142857 |
0,13541 |
|
3 |
0,28 |
1,235 |
0,955 |
7 |
0,142857 |
0,149589 |
|
4 |
1,235 |
2,515 |
1,28 |
7 |
0,142857 |
0,111607 |
|
5 |
2,515 |
3,955 |
1,44 |
7 |
0,142857 |
0,099206 |
|
6 |
3,955 |
4,525 |
0,57 |
7 |
0,142857 |
0,250627 |
|
7 |
4,525 |
5,90 |
1,375 |
7 |
0,142857 |
0,103896 |
Вычислим точечные оценки числовых характеристик.
Состоятельная оценка математического ожидания:
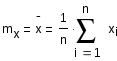
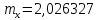
Несмещенная состоятельная оценка дисперсии:
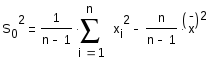
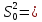5,005457
Несмещенная состоятельная оценка среднеквадратического отклонения:
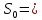2,237288
Вычислим интервальные оценки математического ожидания и дисперсии с надежностью =0.95.
Доверительный интервал для математического ожидания.
Согласно центральной предельной теореме при достаточно большом n закон распределения можно считать нормальным, поэтому воспользуемся следующей формулой для случайной величины X с неизвестным законом распределения:
где z=arg(/2)=arg(0.475)=1.96 - значение аргумента функции Лапласа, тогда интервал равен:
Доверительный интервал для дисперсии:
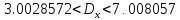
По виду графика эмпирической функции
распределения
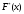и
гистограмм выдвигаем двухальтернативную
гипотезу о законе распределения случайной
величины X:
H0 – величина X распределена по нормальному закону:
где
m и σ - параметры распределения:
;
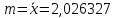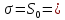2,237288.
H1 – величина X не распределена по нормальному закону:
Проверим гипотезу о нормальном законе по критерию Пирсона 2. Вычислим значение критерия 2 на основе равноинтервального статистического ряда:
Теоретические вероятности попадания в интервалы вычислим по формуле:
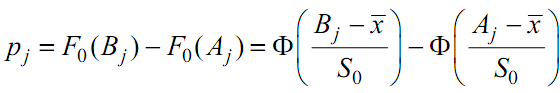
Данные для расчета теоретических вероятностей представлены в таблице:
|
i |
Ai |
Bi |
F0(Ai) |
F0(Bi) |
pj |
pj* |
((pj*-pj)^2)/pj |
|
1 |
-1,23 |
-0,21 |
0 |
0,158605 |
0,158605 |
0,22449 |
0,027368934 |
|
2 |
-0,21 |
0,81 |
0,158605 |
0,292898 |
0,134293 |
0,142857 |
0,000546117 |
|
3 |
0,81 |
1,83 |
0,292898 |
0,464276 |
0,171378 |
0,183673 |
0,000882183 |
|
4 |
1,83 |
2,84 |
0,464276 |
0,642669 |
0,178394 |
0,040816 |
0,106099746 |
|
5 |
2,84 |
3,86 |
0,642669 |
0,794141 |
0,151472 |
0,081633 |
0,032200569 |
|
6 |
3,86 |
4,88 |
0,794141 |
0,899048 |
0,104907 |
0,22449 |
0,136312139 |
|
7 |
4,88 |
5,90 |
0,899048 |
1 |
0,100952 |
0,102041 |
1,17376E-05 |
|
|
|
|
|
Сумма: |
1 |
1 |
0,303421425 |
Вычислим критерий Пирсона:
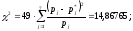
Определим число степеней свободы:
Выбираем критическое значения критерия Пирсона из таблицы для степени свободы k=7 и заданного уровня значимости =0.05:
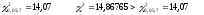
Так как условие не выполняется, то гипотеза H0 о нормальном законе распределения отклоняется.
Проверим гипотезу с помощью критерия Колмогорова. Выберем все значения из вариационного ряда для данного критерия и вычислим значения гипотетической функции:
|
Номер |
Xi |
F*(Xi) |
F0(Xi) |
Z |
|
1 |
-1,23 |
0,020408 |
0,072768 |
0,05236 |
|
2 |
-1,07 |
0,040816 |
0,083185 |
0,042368 |
|
3 |
-1,06 |
0,061224 |
0,083871 |
0,022647 |
|
4 |
-1,05 |
0,081633 |
0,084562 |
0,002929 |
|
5 |
-0,92 |
0,102041 |
0,093933 |
0,008108 |
|
6 |
-0,90 |
0,122449 |
0,09544 |
0,027009 |
|
7 |
-0,88 |
0,142857 |
0,096965 |
0,045892 |
|
8 |
-0,67 |
0,163265 |
0,114068 |
0,049198 |
|
9 |
-0,67 |
0,183673 |
0,114068 |
0,069606 |
|
10 |
-0,58 |
0,204082 |
0,12202 |
0,082062 |
|
11 |
-0,25 |
0,22449 |
0,15447 |
0,07002 |
|
12 |
0,08 |
0,244898 |
0,192164 |
0,052734 |
|
13 |
0,23 |
0,265306 |
0,211015 |
0,054291 |
|
14 |
0,25 |
0,285714 |
0,213608 |
0,072106 |
|
15 |
0,31 |
0,306122 |
0,221497 |
0,084625 |
|
16 |
0,43 |
0,326531 |
0,237765 |
0,088765 |
|
17 |
0,57 |
0,346939 |
0,257545 |
0,089394 |
|
18 |
0,75 |
0,367347 |
0,284176 |
0,083171 |
|
19 |
0,84 |
0,387755 |
0,297969 |
0,089787 |
|
20 |
1,18 |
0,408163 |
0,35261 |
0,055553 |
|
21 |
1,23 |
0,428571 |
0,360945 |
0,067626 |
|
22 |
1,24 |
0,44898 |
0,36262 |
0,08636 |
|
23 |
1,48 |
0,469388 |
0,403541 |
0,065846 |
|
24 |
1,56 |
0,489796 |
0,417445 |
0,072351 |
|
25 |
1,56 |
0,510204 |
0,417445 |
0,092759 |
|
26 |
1,77 |
0,530612 |
0,454393 |
0,076219 |
|
27 |
1,78 |
0,55102 |
0,456165 |
0,094856 |
|
28 |
2,38 |
0,571429 |
0,562804 |
0,008625 |
|
29 |
2,65 |
0,591837 |
0,609787 |
0,01795 |
|
30 |
3,21 |
0,612245 |
0,70162 |
0,089375 |
|
31 |
3,62 |
0,632653 |
0,761868 |
0,129215 |
|
32 |
3,67 |
0,653061 |
0,76873 |
0,115669 |
|
33 |
3,76 |
0,673469 |
0,780801 |
0,107331 |
|
34 |
3,90 |
0,693878 |
0,798837 |
0,10496 |
|
35 |
3,92 |
0,714286 |
0,801339 |
0,087054 |
|
36 |
3,99 |
0,734694 |
0,809947 |
0,075254 |
|
37 |
4,07 |
0,755102 |
0,8195 |
0,064398 |
|
38 |
4,08 |
0,77551 |
0,820672 |
0,045162 |
|
39 |
4,11 |
0,795918 |
0,824161 |
0,028243 |
|
40 |
4,32 |
0,816327 |
0,847366 |
0,03104 |
|
41 |
4,35 |
0,836735 |
0,850507 |
0,013773 |
|
42 |
4,45 |
0,857143 |
0,860664 |
0,003521 |
|
43 |
4,60 |
0,877551 |
0,875001 |
0,00255 |
|
44 |
4,66 |
0,897959 |
0,880437 |
0,017523 |
|
45 |
5,07 |
0,918367 |
0,913153 |
0,005214 |
|
46 |
5,26 |
0,938776 |
0,925821 |
0,012955 |
|
47 |
5,64 |
0,959184 |
0,946867 |
0,012317 |
|
48 |
5,70 |
0,979592 |
0,949707 |
0,029885 |
|
49 |
5,90 |
1 |
0,958311 |
0,041689 |
|
|
|
|
макс: |
0,129215 |