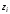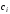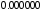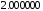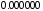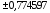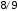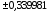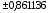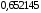- •Вычислительные методы и компьютерная алгебра
- •Общие сведения Сведения об эумк
- •Методические рекомендации по изучению дисциплины
- •Рабочая учебная программа для специальности
- •Пояснительная записка
- •Содержание дисциплины
- •1. Название тем лекционных занятий, их содержание, объем в часах
- •2. Перечень тем лабораторных занятий, их наименование и объем в часах
- •3. Литература
- •3.1. Основная
- •3.2. Дополнительная
- •4. Перечень компьютерных программ, наглядных и других пособий, методических указаний и материалов к техническим средствам обучения
- •Протокол согласования учЕбной программы по изучаемой учебной дисциплине с другими дисциплинами специальности
- •Дополнения и изменения к учебной программе
- •Предисловие ко второму изданию
- •1 Математические модели. Численные методы. Погрешности вычислений
- •1.1 Математические модели и моделирование
- •1.2 Этапы численного решения задач на эвм
- •1.3 Виды погрешностей решения задач
- •1.4 Погрешности арифметических операций
- •1.5 Графы арифметических операций
- •1.6 Распространение погрешностей в вычислениях
- •2 Решение систем линейных алгебраических уравнений
- •2.1 Постановка задачи. Методы решения
- •2.2 Метод Гаусса
- •2.2.1 Описание метода Гаусса
- •2.2.2 Расчетные формулы метода Гаусса
- •2.2.3 Погрешность метода Гаусса. Метод Гаусса с выбором главного элемента
- •2.3 Вычислительная сложность метода Гаусса
- •2.4 Обращение матрицы
- •2.5 Метод lu-разложения
- •2.6 Метод квадратного корня решения симметричных слау
- •2.7 Метод Гаусса–Зейделя
- •2.7.1 Расчетные формулы метода Гаусса–Зейделя
- •2.7.2 Сходимость метода Гаусса–Зейделя
- •2.7.3 Графическая иллюстрация метода Гаусса–Зейделя
- •3 Аппроксимация функций
- •3.1 Понятие аппроксимации функций
- •3.2 Постановка задачи интерполирования функций
- •3.3 Интерполяционный полином Лагранжа
- •3.4 Вычисление значений полиномов
- •3.5 Вычислительная сложность задачи интерполирования
- •3.6 Конечные и разделенные разности функции
- •3.7 Интерполяционный полином Ньютона
- •3.8 Погрешность интерполирования
- •3.9 Полиномы Чебышева 1-го рода
- •3.10 Наилучший выбор узлов интерполирования
- •4 Численное интегрирование
- •4.1 Постановка задачи численного интегрирования
- •4.2 Метод прямоугольников
- •4.3 Погрешность метода прямоугольников
- •4.4 Метод трапеций
- •4.5 Погрешность метода трапеций
- •4.6 Метод Симпсона
- •4.7 Погрешность метода Симпсона
- •4.8 Интерполяционные квадратурные формулы
- •4.9 Интерполяционные квадратурные формулы наивысшей алгебраической степени точности (квадратурные формулы Гаусса)
- •4.9.1 Квадратурная формула Гаусса–Лежандра
- •4.9.2 Квадратурная формула Гаусса–Лагерра
- •4.9.3 Квадратурная формула Гаусса–Эрмита
- •5 Решение нелинейных уравнений
- •5.1 Постановка задачи численного решения нелинейных уравнений
- •5.2 Метод деления отрезка пополам
- •5.3 Метод хорд
- •5.4 Метод простой итерации
- •5.5 Метод Ньютона
- •5.6 Метод секущих
- •6 Решение обыкновенных дифференциальных уравнений
- •6.1 Постановка задачи
- •6.2 Метод рядов Тейлора
- •6.3 Метод Эйлера
- •6.4 Метод Рунге–Кутта 2-го порядка
- •6.5 Метод Рунге–Кутта 4-го порядка
- •7 Решение систем обыкновенных дифференциальных уравнений
- •7.1 Постановка задачи
- •7.2 Приведение дифференциального уравнения -го порядка к системе дифференциальных уравнений 1-го порядка
- •7.3 Метод Эйлера
- •8.2 Выполнение символьных операций в Matlab
- •8.3 Создание символьных переменных
- •8.4 Создание группы символьных переменных
- •8.5 Создание списка символьных переменных
- •8.6 Вывод символьного выражения
- •8.7 Упрощение выражений
- •8.8 Вычисление производных
- •8.9 Вычисление интегралов
- •8.10 Вычисление сумм рядов
- •8.11 Вычисление пределов
- •8.12 Разложение функции в ряд Тейлора
- •8.13 Вычисление определителя матрицы, обращение матрицы
- •9 Дополнение
- •9.1 Вычисление корней полиномов
- •9.2 Решение систем нелинейных уравнений. Метод Ньютона
- •9.3 Решение систем линейных алгебраических уравнений с трехдиагональной матрицей (метод прогонки)
- •9.4 Интерполирование функций сплайнами
- •Практический раздел Указания к выбору варианта
- •Лабораторная работа № 1. Работа в системе Matlab
- •1.1. Цель работы
- •1.2. Порядок выполнения работы
- •Лабораторная работа № 2. Решение систем линейных алгебраических уравнений
- •2.1. Цель работы
- •2.2. Теоретические положения
- •2.3. Порядок выполнения работы
- •Лабораторная работа № 3. Аппроксимация функций
- •3.1. Цель работы
- •3.2. Теоретические положения
- •3.3. Порядок выполнения работы
- •Лабораторная работа № 4. Численное интегрирование
- •4.1. Цель работы
- •4.2. Теоретические положения
- •4.3. Порядок выполнения работы
- •Лабораторная работа № 5. Решение нелинейных уравнений
- •5.1. Цель работы
- •5.2. Теоретические положения
- •5.3. Порядок выполнения работы
- •Лабораторная работа № 6. Решение обыкновенных дифференциальных уравнений
- •6.1. Цель работы
- •6.2. Теоретические положения
- •6.3. Порядок выполнения работы
- •Лабораторная работа № 7. Решение систем обыкновенных дифференциальных уравнений
- •7.1. Цель работы
- •7.2. Теоретические положения
- •7.3. Порядок выполнения работы
- •Лабораторная работа № 8. Выполнение символьных операций
- •8.1. Цель работы
- •8.2. Теоретические сведения
- •8.3. Порядок выполнения работы
- •Литература
- •Литература
4.9 Интерполяционные квадратурные формулы наивысшей алгебраической степени точности (квадратурные формулы Гаусса)
Точность
интерполяционной квадратурной формулы
(4.10) можно существенно увеличить путем
рационального выбора узлов
![]() .
Задача получения более точной квадратурной
формулы формулируется следующим образом:
построить квадратурную формулу
.
Задача получения более точной квадратурной
формулы формулируется следующим образом:
построить квадратурную формулу
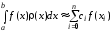 ,
(4.13)
,
(4.13)
которая
при заданном
 была бы точной для полиномов возможно
большей степени. Построение такой
формулы заключается в надлежащем выборе
коэффициентов
была бы точной для полиномов возможно
большей степени. Построение такой
формулы заключается в надлежащем выборе
коэффициентов![]() и узлов
и узлов![]() .
.
Для
решения задачи потребуем, чтобы формула
(4.13) была точна для любого полинома
степени
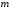 .
Это эквивалентно требованию, чтобы
формула была точна для однородных
полиномов
.
Это эквивалентно требованию, чтобы
формула была точна для однородных
полиномов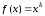 ,
,![]() .
Отсюда получаем условия
.
Отсюда получаем условия
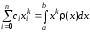 ,
,
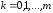 ,
(4.14)
,
(4.14)
которые
представляют собой систему
![]() нелинейных уравнений относительно
нелинейных уравнений относительно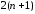 неизвестных
неизвестных![]() ,
,![]() .
Для того, чтобы число уравнений равнялось
числу неизвестных, необходимо выполнение
равенства
.
Для того, чтобы число уравнений равнялось
числу неизвестных, необходимо выполнение
равенства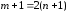 ,
откуда получаем
,
откуда получаем![]() .
Оказывается, что при
.
Оказывается, что при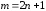 эта система уравнений имеет единственное
решение. Таким образом, существует
квадратурная формула (4.13), точная для
полиномов степени
эта система уравнений имеет единственное
решение. Таким образом, существует
квадратурная формула (4.13), точная для
полиномов степени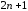 .
Степень точности этой формулы более
чем в 2 раза выше степени точности
интерполяционной квадратурной формулы.
Для получения этой формулы необходимо
определить ее параметры
.
Степень точности этой формулы более
чем в 2 раза выше степени точности
интерполяционной квадратурной формулы.
Для получения этой формулы необходимо
определить ее параметры ,
,![]() путем решения системы нелинейных
уравнений (4.14) при
путем решения системы нелинейных
уравнений (4.14) при![]() .
Однако существует другой путь определения
этих параметров, который содержится в
следующей теореме.
.
Однако существует другой путь определения
этих параметров, который содержится в
следующей теореме.
Теорема.
Квадратурная формула (4.13) точна для
любого полинома степени
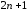 тогда и только тогда, когда выполняются
следующие условия:
тогда и только тогда, когда выполняются
следующие условия:
формула является формулой интерполяционного типа, т.е. ее коэффициенты определяются выражением (4.11);
полином
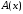 в (4.11) ортогонален с весом
в (4.11) ортогонален с весом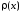 любому многочлену
любому многочлену степени
степени меньше
меньше :
:
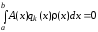 ,
,
 ,
,
что равносильно требованию
 ,
,
 .
(4.15)
.
(4.15)
Теорему принимаем без доказательства.
Замечание
1. Полином
 ,
удовлетворяющий условиям (4.15), называется
ортогональных полиномом на
,
удовлетворяющий условиям (4.15), называется
ортогональных полиномом на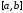 с весом
с весом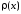 .
.
Замечание
2. Поскольку полином
 имеет вид
имеет вид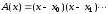
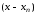 ,
то ясно, что точки
,
то ясно, что точки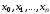 являются корнями этого ортогонального
полинома.
являются корнями этого ортогонального
полинома.
Таким
образом, для любых
 существует, притом единственная,
квадратурная формула наивысшей
алгебраической степени точности
существует, притом единственная,
квадратурная формула наивысшей
алгебраической степени точности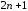 вида (4.13). Узлы этой формулы совпадают
с корнями ортогонального на
вида (4.13). Узлы этой формулы совпадают
с корнями ортогонального на с весом
с весом полинома степени
полинома степени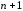 ,
а коэффициенты определяются формулой
(4.11). Интерполяционная квадратурная
формула наивысшей алгебраической
степени точности называется также
квадратурной формулой Гаусса–Кристоффеля
или квадратурной формулой Гаусса. Узлы
,
а коэффициенты определяются формулой
(4.11). Интерполяционная квадратурная
формула наивысшей алгебраической
степени точности называется также
квадратурной формулой Гаусса–Кристоффеля
или квадратурной формулой Гаусса. Узлы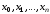 и соответствующие им веса
и соответствующие им веса квадратурной формулы Гаусса рассчитываются
заранее для различных весовых функций
квадратурной формулы Гаусса рассчитываются
заранее для различных весовых функций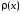 и сводятся в таблицы [8,9]. В следующих
разделах приведены примеры квадратурных
формул Гаусса.
и сводятся в таблицы [8,9]. В следующих
разделах приведены примеры квадратурных
формул Гаусса.
4.9.1 Квадратурная формула Гаусса–Лежандра
Квадратурная
формула Гаусса–Лежандра
используется для вычисления интеграла
с единичной весовой функцией
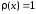 на конечном отрезке
на конечном отрезке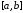 ,
т.е. интеграла вида
,
т.е. интеграла вида
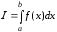 .
.
Этот интеграл линейной заменой переменных
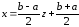
приводится к виду
 .
.
На
отрезке
 ортогональны с весом
ортогональны с весом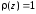 полиномы Лежандра
полиномы Лежандра
 .
.
Первые четыре полинома Лежандра имеют вид
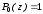 ,
,
 ,
,
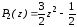 ,
,
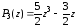 .
.
Узлы
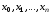 квадратурной формулы в этом случае
выбираются равными корням полинома
Лежандра
квадратурной формулы в этом случае
выбираются равными корням полинома
Лежандра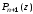 .
Квадратурная формула имеет вид
.
Квадратурная формула имеет вид
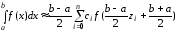 .
.
В таблице 4.1 в качестве примера приведены узлы и коэффициенты для этой формулы при использовании от одного до четырех узлов.
Таблица 4.1 – Узлы и коэффициенты квадратурной формулы Гаусса–Лежандра
|
Число узлов
|
Значения узлов
|
Значения весовых коэффициентов
|
|
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|