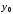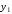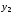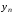- •Вычислительные методы и компьютерная алгебра
- •Общие сведения Сведения об эумк
- •Методические рекомендации по изучению дисциплины
- •Рабочая учебная программа для специальности
- •Пояснительная записка
- •Содержание дисциплины
- •1. Название тем лекционных занятий, их содержание, объем в часах
- •2. Перечень тем лабораторных занятий, их наименование и объем в часах
- •3. Литература
- •3.1. Основная
- •3.2. Дополнительная
- •4. Перечень компьютерных программ, наглядных и других пособий, методических указаний и материалов к техническим средствам обучения
- •Протокол согласования учЕбной программы по изучаемой учебной дисциплине с другими дисциплинами специальности
- •Дополнения и изменения к учебной программе
- •Предисловие ко второму изданию
- •1 Математические модели. Численные методы. Погрешности вычислений
- •1.1 Математические модели и моделирование
- •1.2 Этапы численного решения задач на эвм
- •1.3 Виды погрешностей решения задач
- •1.4 Погрешности арифметических операций
- •1.5 Графы арифметических операций
- •1.6 Распространение погрешностей в вычислениях
- •2 Решение систем линейных алгебраических уравнений
- •2.1 Постановка задачи. Методы решения
- •2.2 Метод Гаусса
- •2.2.1 Описание метода Гаусса
- •2.2.2 Расчетные формулы метода Гаусса
- •2.2.3 Погрешность метода Гаусса. Метод Гаусса с выбором главного элемента
- •2.3 Вычислительная сложность метода Гаусса
- •2.4 Обращение матрицы
- •2.5 Метод lu-разложения
- •2.6 Метод квадратного корня решения симметричных слау
- •2.7 Метод Гаусса–Зейделя
- •2.7.1 Расчетные формулы метода Гаусса–Зейделя
- •2.7.2 Сходимость метода Гаусса–Зейделя
- •2.7.3 Графическая иллюстрация метода Гаусса–Зейделя
- •3 Аппроксимация функций
- •3.1 Понятие аппроксимации функций
- •3.2 Постановка задачи интерполирования функций
- •3.3 Интерполяционный полином Лагранжа
- •3.4 Вычисление значений полиномов
- •3.5 Вычислительная сложность задачи интерполирования
- •3.6 Конечные и разделенные разности функции
- •3.7 Интерполяционный полином Ньютона
- •3.8 Погрешность интерполирования
- •3.9 Полиномы Чебышева 1-го рода
- •3.10 Наилучший выбор узлов интерполирования
- •4 Численное интегрирование
- •4.1 Постановка задачи численного интегрирования
- •4.2 Метод прямоугольников
- •4.3 Погрешность метода прямоугольников
- •4.4 Метод трапеций
- •4.5 Погрешность метода трапеций
- •4.6 Метод Симпсона
- •4.7 Погрешность метода Симпсона
- •4.8 Интерполяционные квадратурные формулы
- •4.9 Интерполяционные квадратурные формулы наивысшей алгебраической степени точности (квадратурные формулы Гаусса)
- •4.9.1 Квадратурная формула Гаусса–Лежандра
- •4.9.2 Квадратурная формула Гаусса–Лагерра
- •4.9.3 Квадратурная формула Гаусса–Эрмита
- •5 Решение нелинейных уравнений
- •5.1 Постановка задачи численного решения нелинейных уравнений
- •5.2 Метод деления отрезка пополам
- •5.3 Метод хорд
- •5.4 Метод простой итерации
- •5.5 Метод Ньютона
- •5.6 Метод секущих
- •6 Решение обыкновенных дифференциальных уравнений
- •6.1 Постановка задачи
- •6.2 Метод рядов Тейлора
- •6.3 Метод Эйлера
- •6.4 Метод Рунге–Кутта 2-го порядка
- •6.5 Метод Рунге–Кутта 4-го порядка
- •7 Решение систем обыкновенных дифференциальных уравнений
- •7.1 Постановка задачи
- •7.2 Приведение дифференциального уравнения -го порядка к системе дифференциальных уравнений 1-го порядка
- •7.3 Метод Эйлера
- •8.2 Выполнение символьных операций в Matlab
- •8.3 Создание символьных переменных
- •8.4 Создание группы символьных переменных
- •8.5 Создание списка символьных переменных
- •8.6 Вывод символьного выражения
- •8.7 Упрощение выражений
- •8.8 Вычисление производных
- •8.9 Вычисление интегралов
- •8.10 Вычисление сумм рядов
- •8.11 Вычисление пределов
- •8.12 Разложение функции в ряд Тейлора
- •8.13 Вычисление определителя матрицы, обращение матрицы
- •9 Дополнение
- •9.1 Вычисление корней полиномов
- •9.2 Решение систем нелинейных уравнений. Метод Ньютона
- •9.3 Решение систем линейных алгебраических уравнений с трехдиагональной матрицей (метод прогонки)
- •9.4 Интерполирование функций сплайнами
- •Практический раздел Указания к выбору варианта
- •Лабораторная работа № 1. Работа в системе Matlab
- •1.1. Цель работы
- •1.2. Порядок выполнения работы
- •Лабораторная работа № 2. Решение систем линейных алгебраических уравнений
- •2.1. Цель работы
- •2.2. Теоретические положения
- •2.3. Порядок выполнения работы
- •Лабораторная работа № 3. Аппроксимация функций
- •3.1. Цель работы
- •3.2. Теоретические положения
- •3.3. Порядок выполнения работы
- •Лабораторная работа № 4. Численное интегрирование
- •4.1. Цель работы
- •4.2. Теоретические положения
- •4.3. Порядок выполнения работы
- •Лабораторная работа № 5. Решение нелинейных уравнений
- •5.1. Цель работы
- •5.2. Теоретические положения
- •5.3. Порядок выполнения работы
- •Лабораторная работа № 6. Решение обыкновенных дифференциальных уравнений
- •6.1. Цель работы
- •6.2. Теоретические положения
- •6.3. Порядок выполнения работы
- •Лабораторная работа № 7. Решение систем обыкновенных дифференциальных уравнений
- •7.1. Цель работы
- •7.2. Теоретические положения
- •7.3. Порядок выполнения работы
- •Лабораторная работа № 8. Выполнение символьных операций
- •8.1. Цель работы
- •8.2. Теоретические сведения
- •8.3. Порядок выполнения работы
- •Литература
- •Литература
2.7.3 Графическая иллюстрация метода Гаусса–Зейделя
Проиллюстрируем сходимость или расходимость метода Гаусса–Зейделя на примере системы уравнений
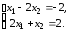
Сразу отметим, что достаточное условие сходимости метода Гаусса–Зейделя (2.29) для данной системы не выполняется, поскольку
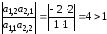 .
.
В соответствии с рекомендациями метода Гаусса–Зейделя перепишем эту систему в виде
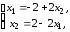
и получим следующие формулы итераций:
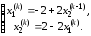 (2.30)
(2.30)
Решение
 данной системы определяется как точка
пересечения двух прямых
данной системы определяется как точка
пересечения двух прямых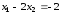 и
и .
Эти прямые изображены на рисунке 2.4. В
соответствии с формулой итераций (2.30)
мы выбираем начальное приближение
.
Эти прямые изображены на рисунке 2.4. В
соответствии с формулой итераций (2.30)
мы выбираем начальное приближение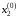 ,
подставляем это значение в первое
уравнение системы
,
подставляем это значение в первое
уравнение системы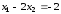 и из него определяем новое приближение
и из него определяем новое приближение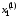 .
Затем это значение
.
Затем это значение подставляем во второе уравнение системы
подставляем во второе уравнение системы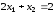 и из него определяем новое приближение
и из него определяем новое приближение .
На этом первая итерация заканчивается.
Далее этот процесс повторяется. Описанные
итерации изображены на рисунке 2.4 прямыми
линиями со стрелками. Мы видим, что
итерационный процесс не сходится к
решению системы.
.
На этом первая итерация заканчивается.
Далее этот процесс повторяется. Описанные
итерации изображены на рисунке 2.4 прямыми
линиями со стрелками. Мы видим, что
итерационный процесс не сходится к
решению системы.
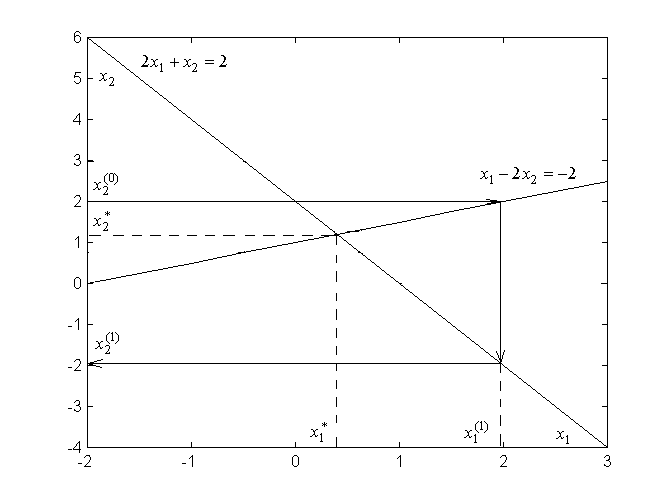
Рисунок 2.4 – Иллюстрация расходимости метода Гаусса–Зейделя
Переставим теперь уравнения системы, т.е. будем решать систему
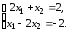
Достаточное условие сходимости метода Гаусса–Зейделя (2.29) теперь выполняется:
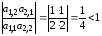 .
.
В соответствии с рекомендациями метода Гаусса–Зейделя перепишем эту систему в виде
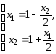
и организуем итерационный процесс по формулам
 (2.31)
(2.31)
Этот процесс изображен прямыми линиями со стрелками на рисунке 2.5.

Рисунок 2.5 – Иллюстрация сходимости метода Гаусса–Зейделя
В
соответствии с формулой итераций (2.31)
выбираем начальное приближение
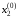 ,
подставляем это значение в первое
уравнение системы
,
подставляем это значение в первое
уравнение системы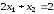 и из него определяем новое приближение
и из него определяем новое приближение .
Затем это значение
.
Затем это значение подставляем во второе уравнение системы
подставляем во второе уравнение системы и из него определяем новое приближение
и из него определяем новое приближение .
Далее этот процесс повторяется. Мы
видим, что процесс сходится. Таким
образом, простой перестановкой уравнений
системы мы добились сходимости метода
Гаусса–Зейделя.
.
Далее этот процесс повторяется. Мы
видим, что процесс сходится. Таким
образом, простой перестановкой уравнений
системы мы добились сходимости метода
Гаусса–Зейделя.
3 Аппроксимация функций
3.1 Понятие аппроксимации функций
Аппроксимация
функции
 – это замена этой функции другой более
простой функцией
– это замена этой функции другой более
простой функцией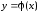 ,
близкой к
,
близкой к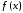 в некотором смысле. В зависимости от
критерия близости функций
в некотором смысле. В зависимости от
критерия близости функций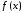 и
и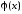 существуют различные методы аппроксимации.
существуют различные методы аппроксимации.
Если
расстояние
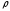 между функциями
между функциями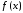 и
и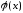 на некотором отрезке
на некотором отрезке действительной прямой определить
выражением
действительной прямой определить
выражением
 ,
,
то
аппроксимация функции
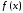 по критерию минимума такого расстояния
по критерию минимума такого расстояния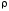 будет называться аппроксимацией с
минимальной интегральной квадратичной
погрешностью.
будет называться аппроксимацией с
минимальной интегральной квадратичной
погрешностью.
Если
критерий близости функций
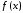 и
и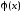 состоит в том, чтобы
состоит в том, чтобы и
и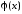 совпадали в дискретном ряде точек
совпадали в дискретном ряде точек отрезка
отрезка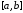 ,
то такой способ аппроксимации функции
,
то такой способ аппроксимации функции называетсяинтерполированием
функции
называетсяинтерполированием
функции
 .
.
Если
расстояние
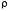 между функциями
между функциями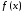 и
и на некотором отрезке
на некотором отрезке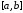 действительной прямой определить
выражением
действительной прямой определить
выражением
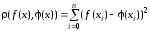 ,
,
то
аппроксимация функции
 по критерию минимума такого расстояния
по критерию минимума такого расстояния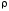 будет называться аппроксимацией по
методу наименьших квадратов.
будет называться аппроксимацией по
методу наименьших квадратов.
3.2 Постановка задачи интерполирования функций
Задача
интерполирования функции
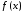 на некотором отрезке
на некотором отрезке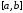 формулируется следующим образом. На
отрезке
формулируется следующим образом. На
отрезке задано
задано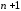 точек
точек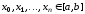 ,
которые называют узлами. Обычно считают,
что первая и последняя точки совпадают
с концами отрезка
,
которые называют узлами. Обычно считают,
что первая и последняя точки совпадают
с концами отрезка :
: ,
, .
Известны значения
.
Известны значения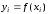 функции
функции в этих точках,
в этих точках,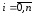 .
Требуется заменить эту функцию некоторой
другой функцией
.
Требуется заменить эту функцию некоторой
другой функцией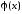 таким образом, чтобы значения обеих
функций совпадали в узлах, т.е. чтобы
выполнялись равенства
таким образом, чтобы значения обеих
функций совпадали в узлах, т.е. чтобы
выполнялись равенства
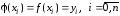 .
.
Искомой
неизвестной в данной задаче является
функция
 .
.
Сформулированную
задачу иногда интерпретируют следующим
образом. Некоторая функция
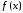 задана на отрезке
задана на отрезке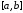 таблицей
своих значений
таблицей
своих значений
|
|
|
|
|
… |
|
|
|
|
|
|
… |
|
и
требуется найти способ определения
значений этой функции в любых других
точках отрезка
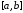 .
.
При
формулировке задачи интерполирования
обычно предполагают, что аппроксимирующая
функция
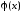 задана с точностью до
задана с точностью до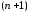 параметров
параметров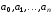 ,
т.е. в виде
,
т.е. в виде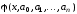 .
Тогда нам необходимо отыскатьнеизвестные
параметры
.
Тогда нам необходимо отыскатьнеизвестные
параметры
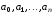 исходя из заданных равенств
исходя из заданных равенств
 .
(3.1)
.
(3.1)
Эти
равенства можно рассматривать как
систему
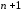 уравнений относительно неизвестных
параметров
уравнений относительно неизвестных
параметров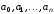 .
.
Чаще
всего функцию
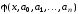 представляют в виде полинома
представляют в виде полинома
 -й
степени
-й
степени
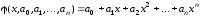 .
(3.2)
.
(3.2)
Тогда система уравнений (3.1) принимает следующий вид:
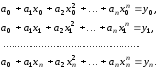 (3.3)
(3.3)
Определитель этой системы имеет вид
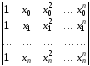
и
называется определителем Вандермонда
на системе точек
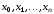 .
Доказано, что если точки
.
Доказано, что если точки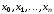 попарно различны, что предполагается
при постановке задачи, то определитель
Вандермонда не равен нулю. В таком случае
система уравнений (3.3) имеет единственное
решение, т.е. существует единственный
полином (3.2) степени
попарно различны, что предполагается
при постановке задачи, то определитель
Вандермонда не равен нулю. В таком случае
система уравнений (3.3) имеет единственное
решение, т.е. существует единственный
полином (3.2) степени ,
коэффициенты которого удовлетворяют
системе уравнений (3.3). Этот полином
называется интерполяционным полиномом
для функции
,
коэффициенты которого удовлетворяют
системе уравнений (3.3). Этот полином
называется интерполяционным полиномом
для функции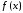 .
.