2.4 Обращение матрицы

Как известно, матрица называется обратной матрице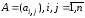, если выполняется соотношение

, (2.13)

где – единичная матрица. Обозначим,,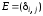, где– символ Кронекера,

Тогда соотношение (2.13) можно записать так:

, . (2.14)

Из этого выражения видно, что если рассматривать -й столбецобратной матрицы как вектор, то он является решением системы линейных алгебраических уравнений (2.14) с матрицейи вектором правой части, все элементы которого равны нулю, кроме-го, который равен 1. Таким образом, элементы обратной матрицы могут быть получены решением системы линейных алгебраических уравнений. Для обращения матрицы необходимо решитьсистем линейных уравнений с одинаковой матрицейи разными правыми частями. Приведение матрицык треугольному виду по формулам (2.8), (2.9) делается при этом только один раз. В дальнейшем необходимо формировать новую правую часть, преобразовывать ее по формуле (2.9) при помощи чисел(2.7) и для каждой правой части выполнять обратный ход. Понятно, что преобразующие числа,, необходимо сохранять по мере их получения на этапе прямого хода. Видно, что эти числа образуют нижнюю треугольную матрицу, совпадающую по размерам с матрицей исключаемых коэффициентов системы. Поэтому число можно поместить на место элемента .

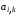Для обращения матрицы этим методом требуется примерно ячеек оперативной памяти и примерноарифметических операций.

Описанный прием вычислений можно применить при решении систем уравнений с одной и той же матрицей и различными правыми частями. В этом случае выгодно привести матрицу к треугольному виду только однажды, используя сохраненные числаво всех последующих вычислениях.

2.5 Метод lu-разложения

Матрица 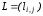,, называется нижней треугольной, если все ее элементы, расположенные выше главной диагонали, равны нулю. Матрица,, называется верхней треугольной, если все ее элементы, расположенные ниже главной диагонали, равны нулю. Общепринятые обозначенияисвязаны с английскими словамиlower(нижний) иupper(верхний). Пусть,,-матрица, например, матрица СЛАУ (2.4). Справедлива следующая теорема.

Теорема. Если все главные миноры квадратной матрицыотличны от нуля, то существуют такие нижняяи верхняятреугольные матрицы, что. Если элементы диагонали одной из матрицилификсированы (ненулевые), то такое разложение единственно.

Получим формулы для разложения матрицы при фиксированной диагонали матрицы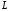. В развернутой форме разложениеимеет вид

.

Выполняя умножение матриц в левой части и приравнивая соответствующие элементы обеих частей равенства, получим -матрицу уравнений

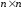относительно-матрицы неизвестных

. (2.15)

Специфика этой системы такова, что позволяет определить неизвестные одно за другим. Сначала из первой строки системы находим

,.

Затем из оставшейся части первого столбца системы находим

,.

Далее, из оставшейся части второй строки

,,

из оставшейся части второго столбца

,,

и т.д. Последним находим элемент

.

Легко заметить, что все отличные от нуля и единицы элементы матриц ,могут быть однозначно вычислены с помощью всего двух формул:

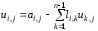,, (2.16)

,. (2.17)

При организации вычислений по формулам (2.16), (2.17) необходимо переключать вычисления с одной формулы на другую, как указано выше. Это удобно делать, ориентируясь на матрицу неизвестных (2.15), а именно, первая строка матрицы (2.15) вычисляется по формуле (2.16) при ,; первый столбец (2.15) (без первого элемента) – по формуле (2.17) при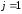,, и т.д.

Если матрица исходной СЛАУ (2.4) разложена в произведение треугольных матриц,, то вместо (2.4) мы можем записать эквивалентное уравнение

.

Введя вектор вспомогательных переменных , перепишем его в виде системы

,

.

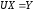Таким образом, решение СЛАУ с квадратной матрицей коэффициентов свелось к решению двух СЛАУ с треугольными матрицами коэффициентов, которые могут быть легко решены. Уравнение в развернутом виде имеет вид

Все могут быть последовательно найдены по формуле

. (2.18)

Уравнение в развернутом виде имеет вид

(2.19)

Отсюда получаем

. (2.20)

Итак, решение СЛАУ методом -разложения сводится к расчетам по четырем формулам: совокупности формул (2.16), (2.17) для получения элементов матриц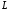и, формуле (2.18) для получения вспомогательного вектораи формуле (2.20) для получения решения СЛАУ.

Отметим, что система уравнений (2.19) полностью совпадает с системой уравнений (2.10), получающейся после завершения прямого хода метода Гаусса. Это означает, что решения СЛАУ с помощью -разложения – это просто другая реализация метода Гаусса. Эта реализация называется схемой Холецкого.

Следует отметить, что в отличие от метода Гаусса схема Холецкого менее удобна для усовершенствования с целью уменьшения влияния вычислительных погрешностей путем выбора подходящих ведущих элементов.