
- •Вычислительные методы и компьютерная алгебра
- •Общие сведения Сведения об эумк
- •Методические рекомендации по изучению дисциплины
- •Рабочая учебная программа для специальности
- •Пояснительная записка
- •Содержание дисциплины
- •1. Название тем лекционных занятий, их содержание, объем в часах
- •2. Перечень тем лабораторных занятий, их наименование и объем в часах
- •3. Литература
- •3.1. Основная
- •3.2. Дополнительная
- •4. Перечень компьютерных программ, наглядных и других пособий, методических указаний и материалов к техническим средствам обучения
- •Протокол согласования учЕбной программы по изучаемой учебной дисциплине с другими дисциплинами специальности
- •Дополнения и изменения к учебной программе
- •Предисловие ко второму изданию
- •1 Математические модели. Численные методы. Погрешности вычислений
- •1.1 Математические модели и моделирование
- •1.2 Этапы численного решения задач на эвм
- •1.3 Виды погрешностей решения задач
- •1.4 Погрешности арифметических операций
- •1.5 Графы арифметических операций
- •1.6 Распространение погрешностей в вычислениях
- •2 Решение систем линейных алгебраических уравнений
- •2.1 Постановка задачи. Методы решения
- •2.2 Метод Гаусса
- •2.2.1 Описание метода Гаусса
- •2.2.2 Расчетные формулы метода Гаусса
- •2.2.3 Погрешность метода Гаусса. Метод Гаусса с выбором главного элемента
- •2.3 Вычислительная сложность метода Гаусса
- •2.4 Обращение матрицы
- •2.5 Метод lu-разложения
- •2.6 Метод квадратного корня решения симметричных слау
- •2.7 Метод Гаусса–Зейделя
- •2.7.1 Расчетные формулы метода Гаусса–Зейделя
- •2.7.2 Сходимость метода Гаусса–Зейделя
- •2.7.3 Графическая иллюстрация метода Гаусса–Зейделя
- •3 Аппроксимация функций
- •3.1 Понятие аппроксимации функций
- •3.2 Постановка задачи интерполирования функций
- •3.3 Интерполяционный полином Лагранжа
- •3.4 Вычисление значений полиномов
- •3.5 Вычислительная сложность задачи интерполирования
- •3.6 Конечные и разделенные разности функции
- •3.7 Интерполяционный полином Ньютона
- •3.8 Погрешность интерполирования
- •3.9 Полиномы Чебышева 1-го рода
- •3.10 Наилучший выбор узлов интерполирования
- •4 Численное интегрирование
- •4.1 Постановка задачи численного интегрирования
- •4.2 Метод прямоугольников
- •4.3 Погрешность метода прямоугольников
- •4.4 Метод трапеций
- •4.5 Погрешность метода трапеций
- •4.6 Метод Симпсона
- •4.7 Погрешность метода Симпсона
- •4.8 Интерполяционные квадратурные формулы
- •4.9 Интерполяционные квадратурные формулы наивысшей алгебраической степени точности (квадратурные формулы Гаусса)
- •4.9.1 Квадратурная формула Гаусса–Лежандра
- •4.9.2 Квадратурная формула Гаусса–Лагерра
- •4.9.3 Квадратурная формула Гаусса–Эрмита
- •5 Решение нелинейных уравнений
- •5.1 Постановка задачи численного решения нелинейных уравнений
- •5.2 Метод деления отрезка пополам
- •5.3 Метод хорд
- •5.4 Метод простой итерации
- •5.5 Метод Ньютона
- •5.6 Метод секущих
- •6 Решение обыкновенных дифференциальных уравнений
- •6.1 Постановка задачи
- •6.2 Метод рядов Тейлора
- •6.3 Метод Эйлера
- •6.4 Метод Рунге–Кутта 2-го порядка
- •6.5 Метод Рунге–Кутта 4-го порядка
- •7 Решение систем обыкновенных дифференциальных уравнений
- •7.1 Постановка задачи
- •7.2 Приведение дифференциального уравнения -го порядка к системе дифференциальных уравнений 1-го порядка
- •7.3 Метод Эйлера
- •8.2 Выполнение символьных операций в Matlab
- •8.3 Создание символьных переменных
- •8.4 Создание группы символьных переменных
- •8.5 Создание списка символьных переменных
- •8.6 Вывод символьного выражения
- •8.7 Упрощение выражений
- •8.8 Вычисление производных
- •8.9 Вычисление интегралов
- •8.10 Вычисление сумм рядов
- •8.11 Вычисление пределов
- •8.12 Разложение функции в ряд Тейлора
- •8.13 Вычисление определителя матрицы, обращение матрицы
- •9 Дополнение
- •9.1 Вычисление корней полиномов
- •9.2 Решение систем нелинейных уравнений. Метод Ньютона
- •9.3 Решение систем линейных алгебраических уравнений с трехдиагональной матрицей (метод прогонки)
- •9.4 Интерполирование функций сплайнами
- •Практический раздел Указания к выбору варианта
- •Лабораторная работа № 1. Работа в системе Matlab
- •1.1. Цель работы
- •1.2. Порядок выполнения работы
- •Лабораторная работа № 2. Решение систем линейных алгебраических уравнений
- •2.1. Цель работы
- •2.2. Теоретические положения
- •2.3. Порядок выполнения работы
- •Лабораторная работа № 3. Аппроксимация функций
- •3.1. Цель работы
- •3.2. Теоретические положения
- •3.3. Порядок выполнения работы
- •Лабораторная работа № 4. Численное интегрирование
- •4.1. Цель работы
- •4.2. Теоретические положения
- •4.3. Порядок выполнения работы
- •Лабораторная работа № 5. Решение нелинейных уравнений
- •5.1. Цель работы
- •5.2. Теоретические положения
- •5.3. Порядок выполнения работы
- •Лабораторная работа № 6. Решение обыкновенных дифференциальных уравнений
- •6.1. Цель работы
- •6.2. Теоретические положения
- •6.3. Порядок выполнения работы
- •Лабораторная работа № 7. Решение систем обыкновенных дифференциальных уравнений
- •7.1. Цель работы
- •7.2. Теоретические положения
- •7.3. Порядок выполнения работы
- •Лабораторная работа № 8. Выполнение символьных операций
- •8.1. Цель работы
- •8.2. Теоретические сведения
- •8.3. Порядок выполнения работы
- •Литература
- •Литература
2.2.3 Погрешность метода Гаусса. Метод Гаусса с выбором главного элемента
Основные
вычисления методом исключений Гаусса
выполняются с помощью формул (2.7) –
(2.9). Граф процесса вычисления коэффициентов
 по формуле (2.8) представлен на рисунке
2.2. Этот граф позволяет проследить
накопление погрешностей в процессе
вычислений по методу Гаусса.
по формуле (2.8) представлен на рисунке
2.2. Этот граф позволяет проследить
накопление погрешностей в процессе
вычислений по методу Гаусса.

Рисунок
2.2 – Граф процесса вычисления коэффициента

Обозначим
 относительную погрешность, содержащуюся
в коэффициенте
относительную погрешность, содержащуюся
в коэффициенте ,
,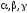 – относительные погрешности округления
соответственно при делении, умножении
и вычитании. Тогда для относительной
погрешности
– относительные погрешности округления
соответственно при делении, умножении
и вычитании. Тогда для относительной
погрешности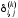 коэффициента
коэффициента можно получить выражение
можно получить выражение
 .
.
Отсюда
получаем формулу для оценки абсолютной
погрешности
 :
:

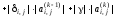 .
.
Если
предположить, что погрешности
 ,
, не превышают некоторой величины
не превышают некоторой величины ,
то получим следующую формулу для оценки
погрешности:
,
то получим следующую формулу для оценки
погрешности:
 .
.
Из
последнего выражения видно, что
погрешность вычисления коэффициента
 в основном определяется первым слагаемым
правой части и уменьшается с уменьшением
в основном определяется первым слагаемым
правой части и уменьшается с уменьшением .
Чтобы
.
Чтобы было по возможности меньшим, необходимо,
чтобы
было по возможности меньшим, необходимо,
чтобы было по возможности большим (см. формулу
(2.7)). Поэтому перед выполнением шага
исключения каждой переменной желательно
переставить уравнения системы так,
чтобы
было по возможности большим (см. формулу
(2.7)). Поэтому перед выполнением шага
исключения каждой переменной желательно
переставить уравнения системы так,
чтобы
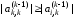 ,
,
 ,
,
потому что тогда
 .
.
Если в методе Гаусса выполняется такая перестановка, то метод называется методом Гаусса с выбором главного элемента. Этот метод имеет меньшую погрешность при определении решения СЛАУ.
Алгоритм Гаусса с выбором главного элемента реализуется с помощью схемы рисунка 2.1 при использовании блока № 5 «Выбор главного элемента». Схема блока № 5 приведена на рисунке 2.3.
2.3 Вычислительная сложность метода Гаусса
Под вычислительной сложностью любого численного метода или алгоритма будем понимать число операций, необходимых для его выполнения. Число операций алгоритма легко посчитать по схеме алгоритма. Выполним такой расчет для метода Гаусса. Число операций будем обозначать числом с индексом, указывающим на вид операции (сложение, вычитание, умножение, деление и т.д.). По схеме рисунка 2.1 для прямого хода получим

 .
.
Приравнивая умножения к делениям и вычитания к сложениям, будем иметь
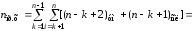


 .
.
Хотя различные операции отличаются по сложности выполнения, но в последних моделях персональных компьютеров путем усовершенствования блока вычислений с плавающей точкой добиваются того, чтобы любая команда с плавающей точкой выполнялась за один такт микропроцессора. Поэтому будем учитывать все выполняемые операции. В итоге получим, что для выполнения прямого хода по методу Гаусса потребуется выполнить
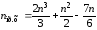
операций. Руководствуясь схемой рисунка 2.1, сделаем аналогичные расчеты для обратного хода:

 .
.
Общее
число операций для выполнения алгоритма
Гаусса без
выбора главного элемента
 будет равно
будет равно
 .
(2.11)
.
(2.11)
В
этом выражении опущено слагаемое, не
зависящее от
 ,
ввиду его малости.
,
ввиду его малости.
Выполним
также расчет числа операций, необходимых
для выбора
главного элемента
 .
Из схемы рисунка 2.3 видно, что здесь
выполняются только операциисравнения
(ср) и присваивания
(пр). Число таких операций будет равно:
.
Из схемы рисунка 2.3 видно, что здесь
выполняются только операциисравнения
(ср) и присваивания
(пр). Число таких операций будет равно:


 .
.
Общее
число операций для выполнения алгоритма
Гаусса с
выбором главного элемента
 будет равно
будет равно
 .
(2.12)
.
(2.12)

Рисунок 2.3 – Схема алгоритма выбора главного элемента
