8Работа. Кинетическая энергия частицы.

Понятия энергии и работы тесно связаны друг с другом.

Кинетическая энергия частицы

  (4)

Приняв во внимание, что произведение mV равно модулю импульса частицы р, выражению (4) можно придать вид

Если сила F , действующая на частицу, не равна нулю, кинетическая энергия получит за время dt приращение

 (5)

где ds - перемещение частицы за время dt.

Величина

называется работой, совершаемой силой F на пути ds (ds - модуль перемещения ds).

Из (5) следует, что работа характеризует изменение кинетической энергии, обусловленное действием силы на движущуюся частицу

dE_k=dA

Если dA = Fds, а , то

. (6)

Проинтегрируем обе части равенства (6) вдоль траектории частицы от точки 1 до точки 2:

.

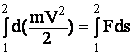Левая часть полученного равенства представляет собой приращение кинетической энергии частицы:

.

Правая часть есть работа А12 силы F на пути 1-2:

Таким образом, мы пришли к соотношению

, (7)

из которого следует, что работа результирующей всех сил, действующих на частицу, идет на приращение кинетической энергии частицы.

9Моменты импульса частицы относительно точки и оси.

Моментом импульса (количества движения) материальной точки А относительно неподвижной точки О называется физическая величина, определяемая векторным произведением:

где r - радиус-вектор, проведенный из точки О в точку A, p=mv - импульс материальной точки (рис. 1); L - псевдовектор, направление которого совпадает с направлением поступательного движения правого винта при его вращении от r к р.

Модуль вектора момента импульса

где α - угол между векторами r и р, l - плечо вектора р относительно точки О.

Моментом импульса относительно неподвижной оси z называется скалярная величина Lz, равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки О данной оси. Момент импульса Lz не зависит от положения точки О на оси z.

При вращении абсолютно твердого тела вокруг неподвижной оси z каждая точка тела движется по окружности постоянного радиуса ri со скоростью vi . Скорость vi и импульс mivi перпендикулярны этому радиусу, т. е. радиус является плечом вектора mivi . Значит, мы можем записать, что момент импульса отдельной частицы равен

и направлен по оси в сторону, определяемую правилом правого винта.

Монет импульса твердого тела относительно оси есть сумма моментов импульса отдельных частиц:

Используя формулу vi = ωri, получим

т. е

Таким образом, момент импульса твердого тела относительно оси равен моменту инерции тела относительно той же оси, умноженному на угловую скорость. Продифференцируем уравнение (2) по времени:

т. е.

Эта формула - еще одна форма уравнения динамики вращательного движения твердого тела относительно неподвижной оси: производная момента импульса твердого тела относительно оси равна моменту сил относительно той же оси.

10 Момент импульса тела, вращающегося вокруг неподвижной оси.

11Момент импульса системы. Закон сохранения момента импульса.

Закон сохранения момента импульса: Если на систему вращающихся вокруг оси тел не действуют моменты внешних сил (система в этом смысле замкнута) или внешние моменты взаимно уравновешиваются, то суммарный момент импульса системы относительно оси вращения с течением времени не изменяется. Таким образом, закон утверждает, что внутренние моменты сил системы не в состоянии изменить полный суммарный момент импульса системы тел, а в состоянии лишь перераспределить его. Внутри системы возможна лишь передача момента импульса от тела к телу.         В аналитическом виде закон сохранения момента импульса записывается следующим образом: если Mвнеш = 0 , то или так: для начального и конечного момента времени