
- •16. Нелинейные косвенные измерения
- •17. Погрешность прямых равноточных измерений.
- •18. Погрешности прямых неравноточных измерений
- •19. Типовые модели экспериментального материала: а) прямые, б) косвенные.
- •20. Оценивая путем минимизации меры расхождения.
- •21. Метод максимального правдоподобия.
- •22. Метод максимума апостериорной плотности вероятности.
- •23. Оценка параметров методом Баейса.
- •24. Оценка для аддитивных моделей. Оценивание при известной матрице ковариации.
- •25. Числа обусловленности.
- •26. Обусловленность задач и вычислений.
- •27. Основная цель анализа ошибок при решении обратных задач
- •28. Эффективность решения обратных количественных задач (три теста).
- •29. Выравнивание методом наименьших квадратов. Пример линейной модели
- •30. Корреляционный анализ
- •Ограничения корреляционного анализа
16. Нелинейные косвенные измерения
Для косвенных измерений при нелинейных зависимостях используют метод линеаризации, предполагающий разложение нелинейной функции в ряд Тейлора

где
 -
нелинейная функциональная зависимость
измеряемой величиныY
от измеренных аргументов ;
-
нелинейная функциональная зависимость
измеряемой величиныY
от измеренных аргументов ;
 -
первая производная от функцииf
по
-
первая производная от функцииf
по
 аргументу,
вычисленная в точках
аргументу,
вычисленная в точках ;
; -
отклонение отдельного результата
измеренияj-го
аргумента от его среднего арифметического;
R
- остаточный член.
-
отклонение отдельного результата
измеренияj-го
аргумента от его среднего арифметического;
R
- остаточный член.
Функция
 разложена
в ряд Тейлора в точке
разложена
в ряд Тейлора в точке ,
знак минус перед членом
,
знак минус перед членом объясняется тем, что
объясняется тем, что ,
а по правилу разложения в ряд Тейлора
должно быть
,
а по правилу разложения в ряд Тейлора
должно быть .
.
Метод
линеаризации допустим, если приращение
функции
 можно заменить ее полным дифференциалом
можно заменить ее полным дифференциалом Остаточным членом
Остаточным членом пренебрегают,
пренебрегают,
если
 .
(5)
.
(5)
Отклонения
 при этом должны быть взяты из возможных
значений погрешности и такими, чтобы
они максимизировали функцию
при этом должны быть взяты из возможных
значений погрешности и такими, чтобы
они максимизировали функцию
Результат измерения при этом может быть определен как
 .
(6)
.
(6)
С.к.о. результата измерения вычисляют по формуле
 .
(7)
.
(7)
17. Погрешность прямых равноточных измерений.
Прямые измерения – это такие измерения, когда значение изучаемой величины находят непосредственно из опытных данных. Для нахождения случайной погрешности опыт необходимо провести несколько раз. Результаты таких измерений, сделанных в одних условиях, на одном приборе и имеющих близкие погрешности называют равноточными
Пусть
в результате kизмерений
величиныx, получен ряд
значенийx1,x2,…,xk.
Как ранее нами было показано, наиболее
близким к истинному значениюx0
измеряемой величиныxявляется среднее арифмитическое
значение: .
Среднее арифметическое часто называют
просто средним значением.
.
Среднее арифметическое часто называют
просто средним значением.
Рассмотрим
вычисление абсолютной погрешности i-го
измерения : Δxi=x0
–xiсуммируя погрешности,
получаем: откуда легко показать, что:
откуда легко показать, что: .
(2)
.
(2)
В
(2) второе слагаемое в правой части при
большом kможно положить
равным нулю, так как всякой положительной
погрешности можно поставить в соответствие
равную ей отрицательную погрешность
тогдаx0= .(3)
Когда число измеренийkмало, тогда равенство (3) приближенно.
.(3)
Когда число измеренийkмало, тогда равенство (3) приближенно.
Иногда
вычисляют среднюю арифметическую
погрешность:
 она определяет пределы, в которых лежит
более половины измерений. Следовательно,
значениеx0 с достаточно
большой вероятностью попадает в интервал
она определяет пределы, в которых лежит
более половины измерений. Следовательно,
значениеx0 с достаточно
большой вероятностью попадает в интервал .
Измерения величиныxтем
точнее, чем меньше величина
.
Измерения величиныxтем
точнее, чем меньше величина .
Абсолютная погрешность результатов
измерений сама по себе еще не определяет
точности измерений. Для более полной
картины необходимо оценивать относительную
погрешность:δX=Δx/
.
Абсолютная погрешность результатов
измерений сама по себе еще не определяет
точности измерений. Для более полной
картины необходимо оценивать относительную
погрешность:δX=Δx/ .
.
18. Погрешности прямых неравноточных измерений
При
измерениях нередко бывают случаи, когда
в одном и том же эксперименте используются
различные приборы, меняются условия
эксперимента, поэтому различные измерения
могут иметь разную точность. Кроме того,
при оценке некоторых величин могут
проводиться эксперименты с разным
количеством экспериментов(серий). Такие
измерения уже нельзя обрабатывать, как
равноточные, так как информация об
искомой величине будет неправильно
интерпретирована. Необходимо в этом
случае использовать все измерения с
учетом их индивидуальной точности.
Пусть имеется ряд значений x1,x2,…,xkизмерений, погрешности которых σ1, σ2,…,
σk. В этом случае дисперсия
наблюдений представима как σ2i=
σ2/giгде σ – неизвестная
величина, которую необходимо найтиgi-
статический вес, или просто вес измерения.
Для данной случайной выборки наиболее
вероятное значение измеряемой величины
есть: а дисперсия:
а дисперсия:
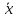 – взвешенное среднее арифмитическое
значение. С учетом этого средняя
квадратическая погрешность вычисляется
по формуле
– взвешенное среднее арифмитическое
значение. С учетом этого средняя
квадратическая погрешность вычисляется
по формуле таким образом в случае неравноточных
измерений вместо среднего фрифмитического
значения и средней квадратической
погрешности одного измерения используются
среднее арифмитическое значение и
средняя квадратическая погрешность
взвешенного среднего значения.
таким образом в случае неравноточных
измерений вместо среднего фрифмитического
значения и средней квадратической
погрешности одного измерения используются
среднее арифмитическое значение и
средняя квадратическая погрешность
взвешенного среднего значения.
