
- •Министерство образования и науки Российской Федерации
- •Глава II. Математический анализ.
- •II семестр
- •Глава I. Неопределенный интеграл
- •Глава II. Определенный интеграл
- •Глава III. Дифференциальные уравнения
- •Глава IV. Кратные, криволинейные и поверхностные интегралы.
- •III семестр
- •Глава I. Основные понятия комплексного анализа
- •Глава II. Интегральное представление аналитической функции.
- •Глава III. Представление аналитических функций рядами.
- •Глава IV. Особые точки. Вычеты и их приложения.
- •Глава V. Ряды и интеграл Фурье.
- •Глава VI. Интегральные преобразования Фурье и Лапласа.
- •IV семестр (теория вероятностей)
- •Глава I. Случайные события.
- •Глава II. Одномерные случайные величины.
- •Глава III. Многомерные случайные величины.
- •Глава IV. Элементы математической статистики
II семестр
Глава I. Неопределенный интеграл
В чем состоит основная задача интегрального исчисления?
Если V(x) производная функция от функции S(x), то как называется функция S(x) по отношению к функции V(x)?
Докажите, что любые две первообразные одной и той же функции отличаются разве лишь на константу.
Дайте определение неопределенного интеграла.
Сформулируйте свойства неопределенного интеграла, вытекающие из его определения.
Какого класса функции имеют первообразную, а потому интегрируемы.
Выучите таблицу интегралов.
Объясните, в чем заключается метод интегрирования подведением под знак дифференциала.
Методы отыскания
 ;
m0,
n0
– целые числа. Одно из них может
равняться нулю.
;
m0,
n0
– целые числа. Одно из них может
равняться нулю.Интегралы от выражений sinxcosx, sinx sinx, cosx cosx.
Интегралы вида
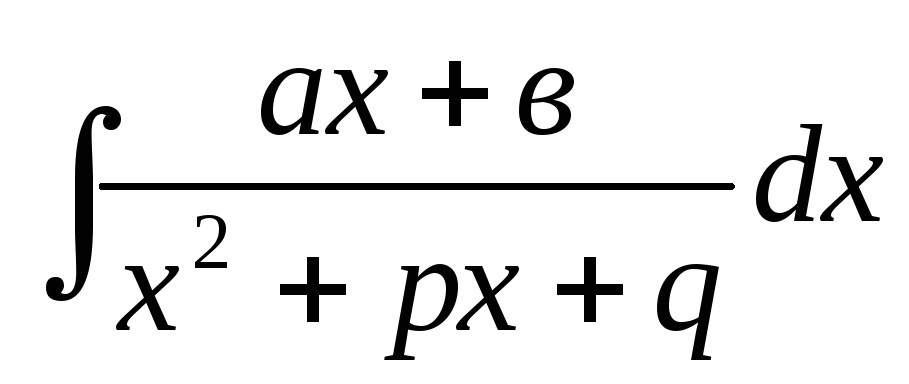 ,
, .
.Формула интегрирования по частям. Приведите примеры интегралов, которые рекомендуется находить, применяя формулу интегрирования по частям.
Какая функция называется дробной рациональной. Дайте определение правильной и неправильной рациональной дроби.
Какие рациональные дроби называются элементарными. Методы их интегрирования.
Как представить правильную дробь в виде суммы элементарных.
Методы отыскания интегралов вида
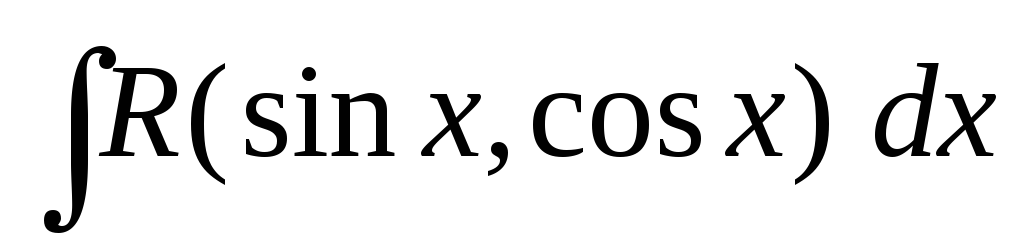 ,
,Методы отыскания интегралов вида
 ,
, .
.Какие замены применяют при вычислении интегралов, содержащих
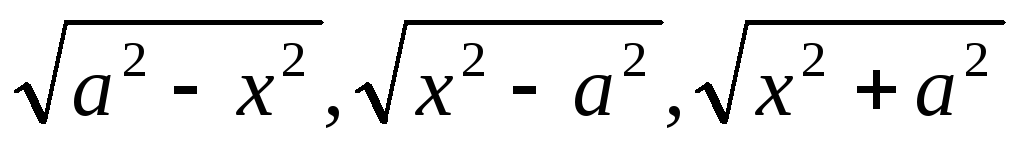
Глава II. Определенный интеграл
Опишите процесс построения интегральных сумм Римана.
Дайте определение интеграла
 .
.В чем заключается геометрический смысл определенного интеграла.
Укажите классы интегральных функций.
Свойства определенного интеграла, выраженные равенствами.
Свойства определенного интеграла, выраженные неравенствами.
Теоремы о среднем.
Сформулируйте и докажите теорему о непрерывности функции
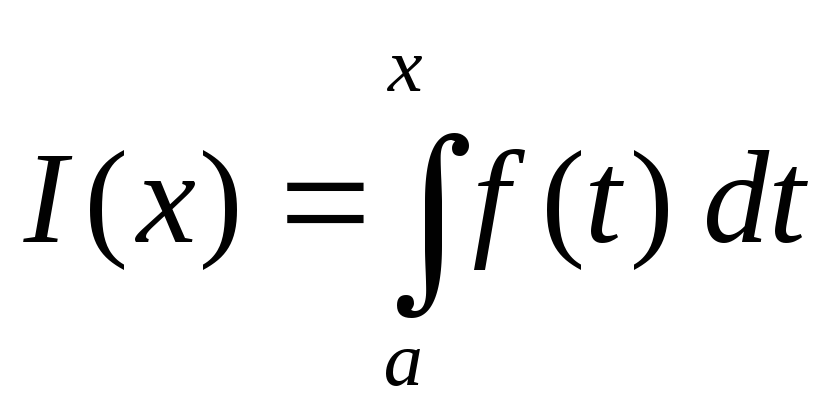 .
.Сформулируйте и докажите теорему о дифференцируемости функции
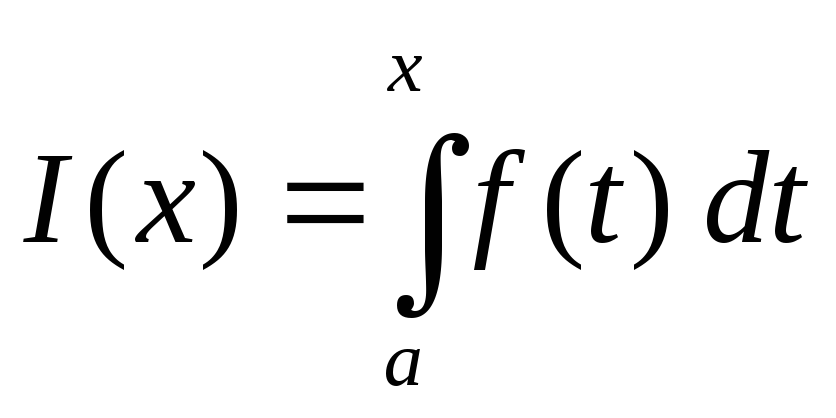 .
.Докажите справедливость формулы Ньютона-Лейбница.
Запишите формулу интегрирования по частям для определенного интеграла.
Сформулируйте теорему о замене переменной в определенном интеграле и докажите ее для непрерывных функций.
Определения несобственных интегралов первого рода на промежутках

Исследование интеграла
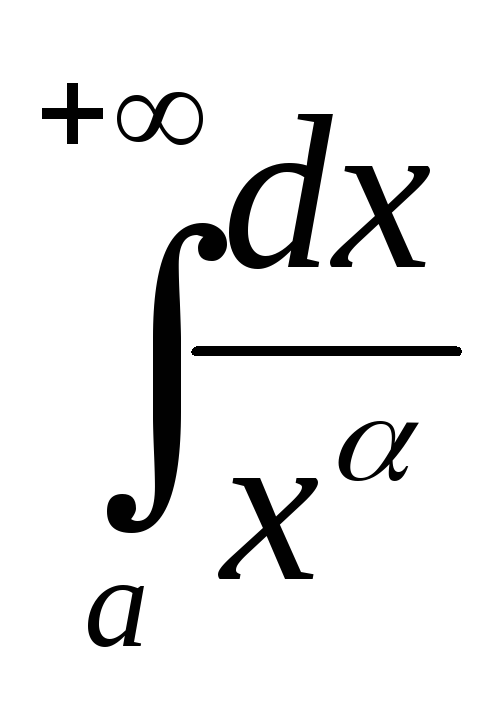 на сходимость в зависимости от значения.
на сходимость в зависимости от значения.Принцип сравнения в конечной форме для
 .
.Принцип сравнения в предельной форме для
 .
.Условная и абсолютная сходимость. Сформулируйте признак Дирихле.
Исследуйте интеграл
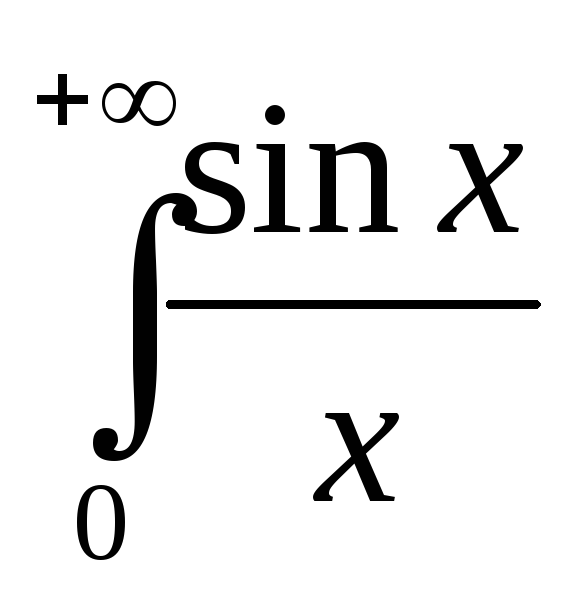 на сходимость.
на сходимость.исследуйте на сходимость интеграл
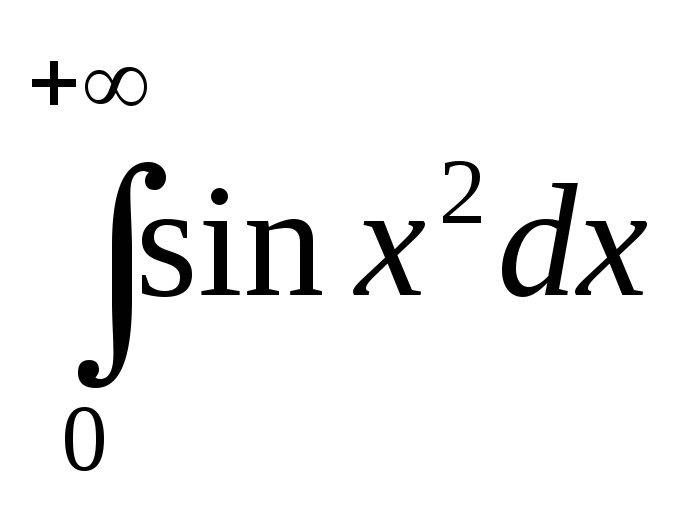 .
.Дайте определение несобственного интеграла второго рода в трех возможных случаях расположения особой точки. Их геометрическая иллюстрация.
Исследовать на сходимость интегралы
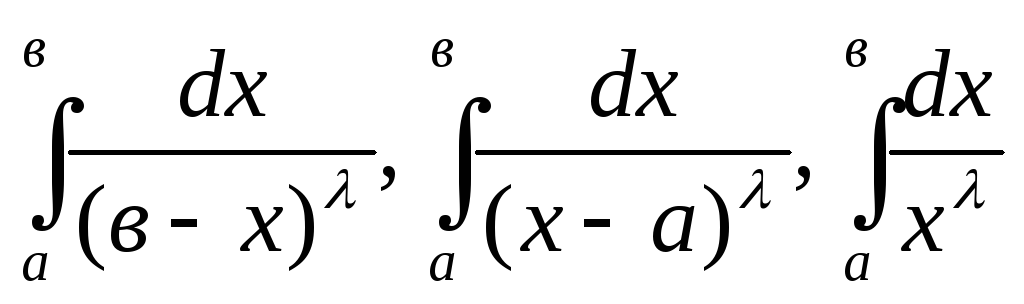 ,
в зависимости от значения.
,
в зависимости от значения.Применение формулы Ньютона-Лейбница для вычислений несобственного интеграла
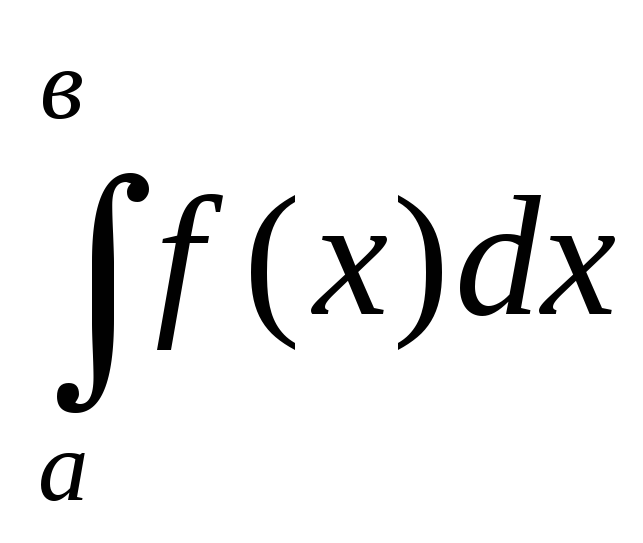
Как решается вопрос о сходимости интеграла
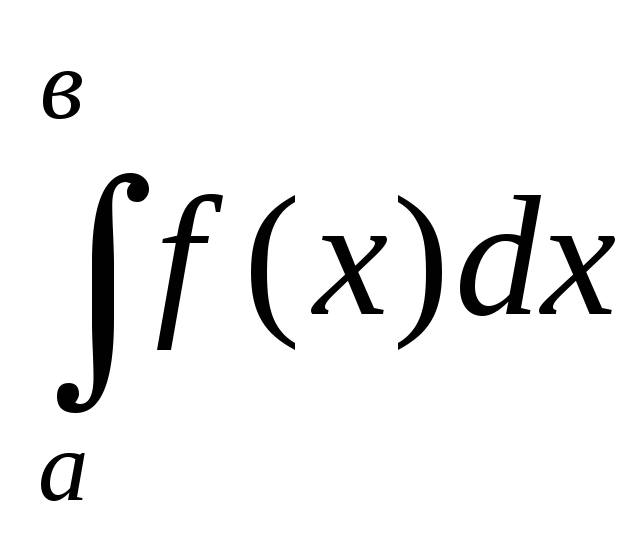 ,
не вычисляя интеграл.
,
не вычисляя интеграл.
