Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Государственный Университет Систем Управления и Радиоэлектроники

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Rukovodstvo_po_resheniju_zadach

.pdf

Скачиваний:

Добавлен:

11.05.2015

Размер:

1.24 Mб

Скачать

☆

1 / 31 2 3 > Следующая >>>

1. ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ

1.1. Основные операции над множествами

Обычно в теории множеств используется пять операций: пересечение, объединение, дополнение, разность и симметрическая разность. Но основными из них являются только пересечение, объединение и дополнение, а оставшиеся две могут быть выражены через основные. Поэтому в данной работе всё внимание сосредоточено только на основных операциях.

Напомним понятия из теории множеств, необходимые для выполнения данной работы. Пересечением множеств A1, A2, A3, …, An называется множество P, содержащее только те

элементы, которые входят в каждое из n множеств:
P = A1 A2 A3 … An,
где – знак, обозначающий операцию пересечения. Например, если
A1 = {1, 2, 3, 4, 5},	A2 = {2, 3, 4, 5, 6, 7}, A3 = {3, 4, 5, 7, 8},	(1)
то

P = A1 A2 A3 = {1, 2, 3, 4, 5} {2, 3, 4, 5, 6, 7} {3, 4, 5, 7, 8} = {3, 4, 5}.

Объединением множеств A1, A2, A3, …, An называется множество Q, в которое входят все элементы множества A1, все элементы множества A2, все элементы множества A3, и так далее до множества An:

Q = A1 A2 A3 … An,

где – знак, обозначающий операцию объединения. Например, в случае множеств (1):

Q = A1 A2 A3 = {1, 2, 3, 4, 5} {2, 3, 4, 5, 6, 7} {3, 4, 5, 7, 8} = {1, 2, 3, 4, 5, 6, 7, 8}.

Все элементы, участвующие в данном рассуждении, образуют множество, называемое уни-

версальным. Условимся обозначать его буквой I.

Дополнением множества A называют множество

A (читается: дополнение множества A), в

котором содержатся все элементы универсального множества I, не входящие в множество A. До-

пустим, что универсальным является множество десятичных цифр

I = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}.

(2)

Тогда для множеств (1) дополнения примут вид:

A1 = {0, 6, 7, 8, 9},

A2 = {0, 1, 8, 9},

A3 = {0, 1, 2, 6, 9}.

Прежде чем приступать к выполнению задания, рекомендуется внимательно рассмотреть

решение задач следующего примера:

Пример 1.

Найдите элементы множеств, полагая, что универсальным является множество (2).

а) P

C A C D A

C ,

б) P B C

A C D A

в) P B

A B D A C D A

C ,

если А = {1, 2, 4, 5}; В = {2, 3, 4, 5, 9}; С = {0, 3, 4, 5, 6, 9}; D = {3, 4, 5, 6, 7}.

Решение.

а) сначала находим дополнения множеств A, B, C и D:

A = {0, 3, 6, 7, 8, 9};

B = {0, 1, 6, 7, 8};

C = {1, 2, 7, 8}. D = {0, 1, 2, 8, 9}.

(3)

Для выражения

C A C D A

находим элементы пересечений:

C = {0, 6};

A C D = {3, 6};

C = {1}.

Применив операцию объединения, получаем:

P = {0, 6} {3, 6} {1} = {0, 1, 3, 6}. Ответ: P = {0, 1, 3, 6};

б) воспользовавшись дополнениями (3), для выражения

P B C D A C D A B C

находим элементы пересечений:
						C = .
B C	D	= {9};	A C D = {4, 5};	A	B	C = .
Объединим эти множества:
P = {9} {4, 5} = {4, 5, 9}.
Ответ: P = {4, 5, 9};
в) для множества

P B D A B D A C D A B C

находим элементы пересечений на основе множеств (3):

D = ;

= {2, 9};

A B D = {3};

C = {1}.

В результате применения операции объединения получаем:

P = {2, 9} {3} {1} = {1, 2, 3, 9}.

Ответ: P = {0, 1, 3, 6};

P = {4, 5, 9}; P = {1, 2, 3, 9}.

1. 2. Подмножества.

Пусть даны множества P и Q. Если все элементы множества P одновременно являются и

элементами множества Q, то множество P называют подмножеством множества Q. Обратимся к

диаграмме Венна, изображённой на рис. 1, где кругами обозначены множества P и Q. Из диаграм-

мы видно, что если область P Q пуста, то множество P окажется внутри множества Q (рис. 2).

Для выяснения того, является ли множество P, заданное неко-

торой формулой, подмножеством множества Q, также представ-

ленного формулой, можно найти элементы множеств P и Q и про-

верить, все ли элементы множества P являются в то же время эле-

ментами множества Q.

Пример 1. Пусть множества P и Q заданы с формулами:

Рис. 1

P A B C

(1)

где

Q A B B

B C;

(2)

A = (0, 2, 4, 5, 9);

(3)

B = (0, 1, 5, 6, 8);

(4)

C = (0, 1, 3, 4, 8),

(5)

I = (0, 1, 2, 3, 4, 5, 6, 7, 8, 9).

Рис. 2

Выясним, является ли множество P подмножеством множества

Сначала найдём элементы пересечений, из которых состоит множество Q:

A B = {0, 5};

P B

= {5, 6};

A B C = {3}.

Находим элементы множества Q, объединив полученные множества:

Q = {0, 3, 5, 6}.

Точно так же найдём элементы множества P:

A B C = {0};

A B C = {6};

P = {0, 6}.

Элементы множеств P и Q найдены. Из записей множеств видно, что элементы 0, 6 P од-

новременно являются и элементами множества Q.

Следовательно, P Q, т.е. множество P есть подмножество множества Q.

Пример 2. Определить, является ли множество R подмножеством множества Q, если Q зада-

но выражением (2), а множество R представлено формулой

R A B

(6)

где множества A, B, C заданы выражениями (3), (4) и (5).

Элементы множества Q уже найдены (см. предыдущий пример): Q = {0, 3, 5, 6}. Находим элементы множества R:

A B = {0, 5}; A C = {1, 3, 8}; R = {0, 1, 3, 5, 8}.

Из выражения R = {0, 1, 3, 5, 8} видно, что во множество R входят элементы 1 и 8, которых нет в множестве Q, т.е. не все элементы множества R являются элементами множества Q, следовательно, множество R не является подмножеством множества Q.

Пример 3. Элементы множеств A, B, C, образующих формулы P и Q, могут быть не заданы. В этом случае для определения того, что P Q, необходимо упростить множество P Q , приме-

няя теоремы поглощения, склеивания и де Моргана. Если получится пустое множество, то P Q. Проиллюстрируем это на примере выражений (1) и (2):

P Q = ( A B C A B C ) A B B C A B C =

(7)

= (A B C A B C ) (A B) (B C) (A B C ) =

(8)

= (A B C A B C ) (A B A C B B C) (A B C ) =

(9)

= (A B C

) (

C) (A B

) = .

(10)

В формуле (7) множества P и Q представлены в развёрнутом виде согласно выражениям (1) и

(2). В (8) применена теорема де Моргана. В (9) частично раскрыты скобки выражения, полученного в результате применения теоремы де Моргана. В (10) применена теорема поглощения. Если в

(10) раскрыть скобки, то получим пустое множество. Отсюда вывод: так как P Q = , то мно-

жество P является подмножеством множества Q: P Q.

Этот результат получен при отсутствии сведений о том, из каких элементов состоят множества A, B и C. Очевидно, что множества A, B и C могут состоять из любых элементов – результат будет тот же самый. Информация о содержании множеств A, B и C, может потребоваться только в

том случае, если в результате упрощения выражения P Q окажется, что P Q . Однако в

данной главе такие случаи не рассматриваются.

В нижеприведённых заданиях множества P и Q заданы только формулами, в которых операциями объединения, пересечения и дополнения связаны множества A, B, C и D, а из каких элементов состоят множества A, B, C и D, не указано. Поэтому во всех случаях, когда в результате упро-

щения выражения P Q получается пустое множество, необходимо считать, что P Q. Если же P Q , то множество P не является подмножеством множества Q.

Все нижеприведённые задания с дидактической точки зрения эквивалентны. Поэтому для разъяснения того, как их выполнять, вполне достаточно одного примера:

Пример 4. Укажите номера множеств, которые являются подмножествами множества

Q A D B C A B C.

1) P A B B C B D;

2) P A

D B

3) P

C D;

4) P A B B C;

5) P A D

6) P A B C

C B C

;

7) P A C D

C B C D;

8) P A B

B D.

Решение.

Сначала по теореме де Моргана находим множество Q :

Q = (A D) (B C ) (A B C).

Раскроем скобки и упростим:

Q = A B D A B C B C D A B C.

Находим множество P Q для каждого из восьми заданных множеств:

1) P Q = ( A B B C B D) (A B D A B C B C D A B C).

Раскроем скобки и упростим:

P Q = A B C A B D.

Это выражение получено в результате упрощения с применением теоремы поглощения. Далее упростить его невозможно, следовательно P Q , т.е. первое множество не является подмножеством множества Q;

2) P Q = (A C D B C D) (A B D A B C B C D A B C).

Раскроем скобки. В результате получим: P Q = , следовательно, P Q, т.е. второе множество из восьми заданных является подмножеством множества Q;

3) P Q = (A B C B C D) (A B D A B C B C D A B C).

И в этом случае, если раскроем скобки, то получим пустое множество. Следовательно, третье множество также является подмножеством множества Q;

4) P Q = ( A B B C) (A B D A B C B C D A B C).

Здесь первый же этап в раскрытии скобок даёт выражение вида

(A B) (A B D) = A B D ,

откуда следует, что четвёртое множество не является подмножеством множества Q; 5) (A D B C B C D) (A B D A B C B C D A B C).

Раскрыв скобки, получим выражение A B C D. Отсюда следует, что пятое множество не является подмножеством множества Q;

6) (A B C B D) (A B D A B C B C D A B C).

Здесь, как и в случае четвёртого множества, первый же шаг в раскрытии скобок приводит к выводу о том, что шестое множество не является подмножеством множества Q;

7) (A C D B C B C D) (A B D A B C B C D A B C).

Раскрыв скобки, получим пустое множество, следовательно, седьмое множество является подмножеством множества Q;

8) (A B C B D) (A B D A B C B C D A B C) = A B D.

Так как A B D 0, то данное множество не является подмножеством множества Q.

Таким образом, множества 2, 3, и 7 есть подмножества множества Q.

Ответ: 2, 3, 7.

1.3. Диаграммы Венна

Диаграммы Венна обеспечивают возможность наглядного представления отношений между множествами и во многих случаях позволяют значительно сократить трудозатраты при выполнении теоретико-множественных операций. Проиллюстрируем это на примере.

Найти элементы множества

P A

C A

C A B C A

(1)

при условии, что

А = {1,4,5,8}; В = {1,2,3,5,7}; С = {2,3,5,6,9}; I = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}.

Эту задачу можно решить способом, изложенным в подразделе 1.1. Однако с применением диаграмм Венна решение можно получить гораздо быстрее.

Построим диаграмму Венна и нанесём на неё элементы заданных множеств (рис. 1).

A	8			B
	8	1	7
4		1	7
4		5	3
		5	3
			2	C
0		6	9
0				I
				I

Рис. 1

Элемент 0 не входит ни в одно из заданных множеств. Записываем его вне кругов, но в пределах квадрата. Цифра 1 входит в множества A и B, но не входит в множество C. Находим область на пересе-

чении множеств A, B и C , и записываем в неё цифру 1. Элемент 2 записываем в область на пересечении множеств A, B и C, и т.д. до цифры 9, которую записываем на пересечении множеств A, B и C.

Теперь обращаемся к множеству (1). В области A B C находятся элементы 4 и 8, область A B C пуста, в области A B C

находится элемент 7, в области A B C – элементы 6 и 9. Таким

A	1	B
	1
8	4 7

образом, ответом является выражение

C P = {4, 6, 7, 8, 9}.

3 9

Рассмотрим ещё один пример. Найдём элементы множества

P A B C A B C A B C A B C

Рис. 2

при условии, что

А = {0,4,6,7,8};

В = {1,4,5,7}; С = {0,2,3,5,6,9}; I = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}.

Диаграмма Венна приведена на рис. 2. По этой диаграмме находим ответ:

P = {0, 2, 3, 5, 6, 8, 9}.

1.4. Отношения включения

Упрощение теоретико-множественных формул обычно осуществляется с применением теорем поглощения и склеивания. Однако во многих случаях упрощение может быть продолжено, если между множествами заданы какие-либо отношения: равенства, включения и др. Проиллюстрируем это на примере множества, заданного следующей формулой:

P A B C B C

A C D A

C B C D.

(1)

Упростим формулу (1) с применением теорем поглощения и склеивания:

P B C B D A

C A C D.

(2)

Это множество состоит из четырёх составляющих:

1) B C;

2) B D;

3) A

C ;

4) A C D.

Предположим, что множества A, B, C, D связаны отношениями

включения следующим образом:

A B C D I,

(3)

где I – универсальное множество (рис. 1).

Рассмотрим первую составляющую B C множества (2). Если B

C, то

Рис. 1

B C = B.

Это видно из рис. 2, где показано, что множество B (с вертикальной

штриховкой) является подмножеством множества C, обозначенного гори

зонтальной штриховкой. Множество B C заштриховано и горизонталь

ной и вертикальной штриховками.

Двойная

штриховка

одновременно

обозначает и множество B, следовательно, B C = B.

Аналогичное утверждение справедливо и для второй составляющей

Рис. 2

множества (2), т.е. если B D, то

B D = B,

а также для четвёртой: если C D, то

C D = C и

C D

Более

сложным является

случай с

третьей

составляющей

C . Выделим из неё пересечение A

. На рис. 3 горизонтальной Рис. 3

штриховкой обозначено множество A, вертикальной – множество B. Из

рис. 3 видно, что если A B, то

A B = ,

поскольку области множеств A и B не пересекаются (не пересекаются

области множеств A и

). Но если A

= , то и

= .

Таким

образом, для всех

четырёх составляющих

множества

(2)

найдены упрощённые представления. Подставим их в (2):

Рис. 4

P B C B D A B C A C D =


= B B	A	C B	A	C.	(4)

Нанесём это выражение на диаграмму Венна (рис. 4). Область B на диаграмме обозначена

вертикальной штриховкой, область A C – горизонтальной. Заштрихованной является вся область C, следовательно,

B A C C.

Такой же результат из выражения (4) можно получить и алгебраически. Прежде всего, отметим, что, так как A B C, то

B B C.

(5)

Тогда выражение (4) преобразуется следующим образом:

C B

C = B

B B C

B (I

) C (

B) B C C.

Таким образом, минимальное выражение (2) с учётом (3) имеет вид P C.

Рассмотрим ещё один пример 2. Пусть требуется упростить выражение

P A B C

C D A C D

(6)

с учетом отношений включения (3).

Так как A B C, то первая составляющая множества (6) примет вид

A B C A.

Так как B C, то

Аналогично, поскольку A C, то

Подставим полученные выражения в (6):

P A B C B C D A C D A C D C D A C D.

Это и есть минимальное выражение для множества (6), полученное с учётом отношений включения (3).

Ответ: A C D.

2. БУЛЕВЫ ФУНКЦИИ

2.1.Нормальные формы булевых функций

Кнормальным формам булевых функций относятся все те формулы, которые представлены в дизъюнктивной нормальной форме (ДНФ), т.е. заданы дизъюнкцией конъюнкций (суммой произведений), либо в конъюнктивной нормальной форме (КНФ), т.е. в виде конъюнкции дизъюнкций. При этом в ДНФ кроме конъюнкций могут входить и отдельные буквы. То же самое относится и к КНФ, т.е. в формулах, представленных в КНФ, наряду с дизъюнкциями могут находиться и отдельные переменные, не связанные знаками дизъюнкции с другими переменными. Примеры нормальных форм:

1)f (A, B, C) AB AB C (дизъюнктивная нормальная форма);

3)f (P, Q, R) (P Q)R (конъюнктивная нормальная форма);

2)f (A, B,C, D) (B C D)(C D)(A C D) (конъюнкция дизъюнкций, т.е. КНФ);

4)f (A, B) A B (эта форма является одновременно и ДНФ и КНФ);

5)f B (и эта форма является одновременно и ДНФ и КНФ);

6)f 1 (функция константа единица относится к нормальным формам);

7)f 0 (функция константа нуль также относится к нормальным формам).

Не относятся к нормальным формам:

1) f ( A, B, C) AB AB C. Первое слагаемое не является конъюнкцией. Функция задана в форме третьего порядка;

2) f (A, B,C, D) (BD C D)(C D)(A C D). К нормальным формам эта функция не от-

носится, так как она имеет третий порядок: в первом скобочном выражении кроме отдельных аргументов находится конъюнкция;

3)f (A, B, C) AB A(B C). Второе слагаемое не является конъюнкцией отдельных переменных. Эта функция также представлена в форме третьего порядка;

4)f ( A, B) AB. К нормальным формам это выражение не относится, так как хотя оно имеет

второй порядок, но не является дизъюнкцией конъюнкций и не является конъюнкцией дизъюнкций;

5)f ( A, B) A B. Как и в предыдущем случае к нормальным формам это выражение не относится;

6)f ( A, B, C, D) AB AC ACD. Если удалить знак инверсии, то останется ДНФ. Со знаком

же инверсии это выражение относится к формам третьего порядка.

Совершенной дизъюнктивной нормальной формой (СДНФ) функции n переменных называется такая форма, когда все входящие в неё конъюнкции есть минтермы, где под минтермом понимается такая конъюнкция n переменных, в которую каждая переменная входит один раз в прямой или в инверсной форме. Например:

f (A, B, C, D) ABCD ABCD ABCD ABCD.

Эта функция зависит от четырёх переменных. Каждая конъюнкция является минтермом, так как содержит по одному разу все переменные, от которых зависит функция. Следовательно, функция представлена в СДНФ.

Функция, заданная одиночной конъюнкцией, например, вида f (A, B, C, D) ABCD,

также относится к классу СДНФ. Хотя она состоит лишь из одной конъюнкции, но эта конъюнкция является минтермом.

В отличие от этого выражения функция

f(A, B, C, D) ABD

кСДНФ не относится, так как в неё входит фиктивный аргумент C. Она представлена в минимальной ДНФ.

Функция вида

f(A, B,C, D) ABC ABC ADC ABC

внешне напоминает СДНФ, поскольку все конъюнкции состоят из одних и тех же букв с инверсиями или без инверсий. Но к СДНФ это выражение не относится, поскольку функция зависит от четырёх переменных, а в конъюнкции входят только по три аргумента.

Совершенной конъюнктивной нормальной формой (СКНФ) функции n переменных называется такая форма, когда все входящие в неё конъюнкции есть макстермы, где под макстермом понимается такая дизъюнкция n переменных, в которую каждая переменная входит один раз в прямой или инверсной форме. Например, функция

f (A, B,C, D) (A B C D)(A B C D)(A B C D),

зависящая от четырёх переменных, представлена в СКНФ. Её скобочные выражения представляют собой макстермы, так как все переменные входят в каждое из этих скобочных выражений по одному разу.

К классу СКНФ относится и выражение f (A, B,C, D) A B C D,

хотя в нём нет скобок. В дизъюнкцию A B C D входят все переменные заданной функции, следовательно, эта дизъюнкция является макстермом. Функция вида

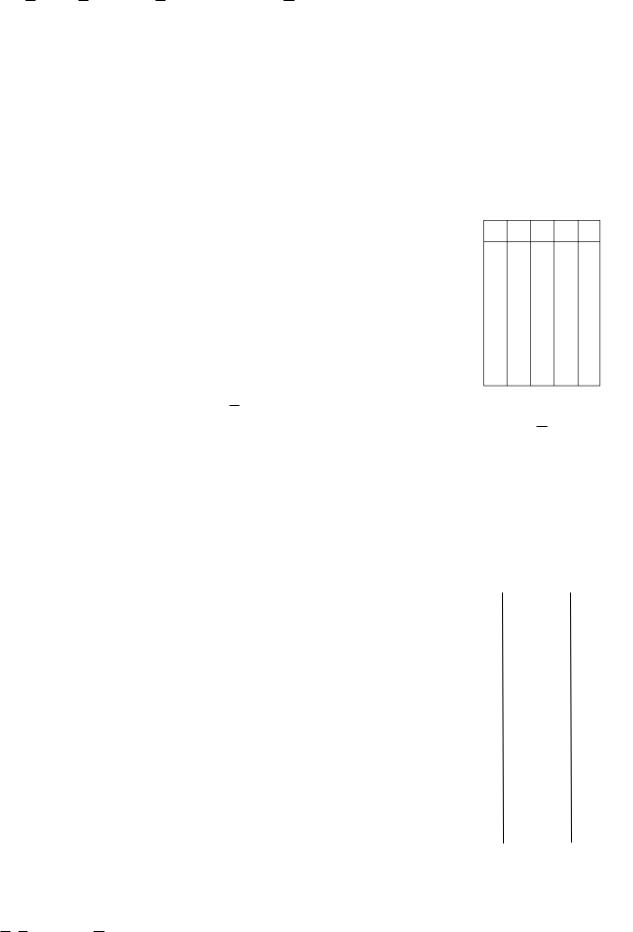
f(A, B,C, D) (A B C D)(A B C D)(A B C )

кСКНФ не относится, так как последнее скобочное выражение содержит только три переменные, следовательно, макстермом оно не является.

2.3. Совершенные дизъюнктивные нормальные формы булевых функций

Булеву функцию можно представить в СДНФ при помощи теоремы разложения Шеннона (как в предыдущем подразделе). Однако нередко для нахождения СДНФ функции проще вос-

пользоваться таблицей истинности.

Пример 1. Представить функции в СДНФ. Номера минтермов упорядочить по возрастанию.

	f (A, B,C)
1)		A	BC			;					Таблица 1
2)	f (A, B,C, D) A BC D;								R	A	B	C	f
3)	f ( A, B,C, D) AB(D CD AC);								0	0	0	0	1
									1	0	0	1	1
4)	f (A, B,C, D)			A	(BC		D ABCD	ABCD);
									2	0	1	0	1
5)	f (A, B,C, D) AD AC BC.
									3	0	1	1	1
Решение.
									4	1	0	0	0
Первая функция зависит от трёх переменных, следовательно, строим
									5	1	0	1	0
таблицу с тремя колонками A, B, C и в строках записываем двоичные наборы
									6	1	1	0	1

значений переменных (табл. 1). Слева расположим колонку R для записи де-									7	1	1	1	0
сятичных эквивалентов двоичных наборов.

Заполняем колонку f. Первое слагаемое A равно единице при A = 0. Следовательно, в колонке f ставим единицы в строках с номерами 0–4, т.е. там, где A = 0. Второе слагаемое BC равно единице при B = 1 и C = 0. Находим в таблице строки, в которых B = 1, C = 0. Это строки с номерами 2 и 6. Единицы, расположенные в колонке f, показывают, какие номера минтермов из колонки R образуют искомую СДНФ.

Ответ к первой функции: 0, 1, 2, 3, 6.

Строим таблицу истинности для второй функции (табл. 2). Первое слагаемое этой функции имеет вид A, следовательно, колонку f заполняем единицами на пересечении со строками 8, 9, 10,

11, 12, 13, 14 и 15, т.е. там, где A = 1.						Таблица 2
Слагаемое BC равно единице при B = C = 1. Дополняем колонку f едини-						Таблица 2

цами на пересечении со строками 6 и 7 (в строках 14 и 15 уже стоят единицы,
							A	В C		D	f
поэтому вторично их не ставим). Дополнив единицами колонку f в соответ-						0	0	0	0	0	0
ствии с третьим слагаемым, получаем ответ:						0	0	0	0	0	0
ствии с третьим слагаемым, получаем ответ:						1	0	0	0	1	1
f ( A, B,C, D) A BC D = (1, 3, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15).						1	0	0	0	1	1
						2	0	0	1	0	0
Аналогичным образом находим номера минтермов, образующих СДНФ						3	0	0	1	1	1
оставшихся трёх функций. Третья функция представлена не в ДНФ, поэтому						4	0	1	0	0	0
сначала раскроем скобки. Ответ к третьей функции:						5	0	1	0	1	1
сначала раскроем скобки. Ответ к третьей функции:						6	0	1	1	0	1
f (A, B,C, D) AB(D CD AC) ABD ABCD ABC = (13, 14, 15).						6	0	1	1	0	1
f (A, B,C, D) AB(D CD AC) ABD ABCD ABC = (13, 14, 15).						7	0	1	1	1	1
Четвёртая функция также представлена не в ДНФ. Раскрываем скобки и						7	0	1	1	1	1
						8	1	0	0	0	1
						8	1	0	0	0	1
получаем ответ:						9	1	0	0	1	1
f (A, B,C, D)
f (A, B,C, D)	A	(BC	D ABCD		ABCD) ABCD (5),	10	1	0	1	0	1
т.е. эта функция состоит из единственного минтерма с номером 5.						11	1	0	1	1	1
						12	1	1	0	0	1
Ответ к последней функции:						12	1	1	0	0	1
Ответ к последней функции:						13	1	1	0	1	1
						13	1	1	0	1	1
f (A, B,C, D) AD AC				BC = (6, 7, 8, 9, 11, 12, 13, 14, 15).		14	1	1	1	0	1
В некоторых случаях, когда формула проста, можно ограничиться только						15	1	1	1	1	1
тождественными преобразованиями, т.е. обойтись без таблицы истинности.

Пример 2. Найти СДНФ функции f (A, B,C) A(B AC BC ).

Решение. Раскроем скобки и преобразуем выражение:

f (A, B,C) A(B AC BC ) = AB ABC = AB(C C ) ABC = = A BC A B C ABC = (0, 1, 2).

Ответ: 0, 1, 2.

Пример 3. Найти СДНФ функции f (B,C, N) BCN BCN BCN BCN.

Решение. Это выражение задано в СДНФ. Поэтому чтобы найти ответ, достаточно минтермы заменить соответствующими номерами:

f (B,C, N) BCN BCN BCN BCN (3,6,2,5) (2,3,5,6). Ответ: 2, 3, 5, 6.

3. ПРИМЕНЕНИЕ КАРТ ВЕЙЧА ДЛЯ МИНИМИЗАЦИИ БУЛЕВЫХ ФОРМУЛ 3.1. Минимизация в классе ДНФ булевых функций, заданных в СДНФ

Минимизация булевых формул при помощи карт Вейча сводится к визуальному отысканию простых импликант, но не всех возможных, а только тех, которые в совокупности покрывают все единицы на карте, и при этом количество букв, входящих во все найденные простые импликанты, должно быть наименьшим по сравнению с любыми другими формулами, представляющими заданную булеву функцию. На рис. 1–3 изображены карты Вейча трёх, четырёх и пяти переменных соответственно, в клетках которых записаны номера минтермов, и указаны области действия логических аргументов. Этими картами можно пользоваться при нанесении на них булевых функций, заданных перечнями номеров минтермов.

На рис. 4–33 приведены примеры минимизации булевых формул.

								A									E
								A								A						A

		A				B	12	14			6	4		B	25	29		13	9		24	28		12	8
							13	15			7	5			27	31		15
B	6		7	3	2								D						11		26	30		14	10	D
B	6		7	3	2														11		26	30		14	10
	4		5	1	0		9	11			3	1			19	23		7	3		18	22		6	2
	4		5	1	0		9	11			3	1			19	23		7	3		18	22		6	2
							8	10			2	0			17	21		5	1		16	20		4	0

			C

										C							C						C
		Рис. 1.							Рис. 2.											Рис. 3.

1	1		1	1	1	1		1		1	1		1	1

	1	1		1	1	1	1	1	1		1	1		1

	Рис. 4				Рис. 5			Рис. 6				Рис. 7

1	1	1				1		1	1	1	1		1		1

1	1		1	1	1	1	1		1	1		1	1	1

	1			1		1	1	1		1			1	1	1

1	1		1		1	1		1	1	1	1	1		1

1	1	1	1	1		1	1	1		1				1

1	1	1	1			1	1	1		1	1		1

1	1	1		1	1	1	1	1	1	1	1	1		1

Рис. 24				Рис. 25				Рис. 26				Рис.27

В заданиях для самостоятельной работы все функции заданы в СДНФ. Каждое задание состоит из четырёх функций. Требуется найти их минимальные ДНФ. Для самоконтроля необходимо указать число знаков дизъюнкции минимальной ДНФ и число вхождений переменных. Проиллюстрируем это на примере следующего задания:

а) f (A, B,C) (1, 2, 4, 6, 7).

б) f (A, B,C, D) (1, 2, 3, 4, 5, 6, 8, 9, 12, 13, 15). в) f (A, B,C, D) (5, 6, 7, 10, 11, 12, 13, 15).

г) f (A, B,C, D, E) (7, 9, 10, 11, 12, 13, 14, 15, 18, 22, 23, 26, 27, 30, 31).

Решение.

Минимизируем первое выражение: f (A, B,C) AB AC BC ABC.

В его минимальной ДНФ три знака дизъюнкции и девять вхождений букв. Ответ: 3, 9. Минимизируем второе выражение: f (A, B,C, D) AC ABD ABD ACD BC . Здесь четыре знака дизъюнкции и 13 букв. Ответ: 4, 13.

Минимизируем третье выражение: f (A, B,C, D) BD ABC ABC ABC.

Ответ: 3, 11.

Минимизируем последнее выражение:

f (A, B,C, D, E) BD ABE CDE ADE ABC.

Ответ: 4, 14.

3.2. Минимизация в классе КНФ булевых функций, заданных в СДНФ

1 / 31 2 3 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
25.09.20195.51 Mб1PTI.docx
#
11.05.2015386.05 Кб13q.doc
#
11.05.2015115.2 Кб9Rabochaya_programma_GOS-EKZ_zaochniki.doc
#
11.05.2015424.45 Кб11Rab_progr_210100-12-pre26.doc
#
18.11.20191.11 Mб3Romanenko_metodichka.doc
#
11.05.20151.24 Mб36Rukovodstvo_po_resheniju_zadach.pdf
#
11.05.20151.81 Mб4rule-work-2012.rtf
#
11.05.20151.81 Mб3rule-work-2012.rtf
#
16.03.20162.47 Mб57Sabyrov_N_B_143-M_Disser.docx
#
11.05.2015654.79 Кб10sam_rab_1.pdf
#
11.05.2015959.49 Кб142SAOD..doc