33. 2-3 Деревья. Основные свойства. Высота 2-3 дерева.
Дерево называется 2-3 деревом, если каждый внутренний узел имеет либо 2, либо 3 сына.
Узел имеющий 2 сына называется двухместным. Узел имеющий три сына называется трехместным.
Высота 2-3 дерева, содержащего n узлов, не может быть больше [log(n+1) - 1] (целая часть).
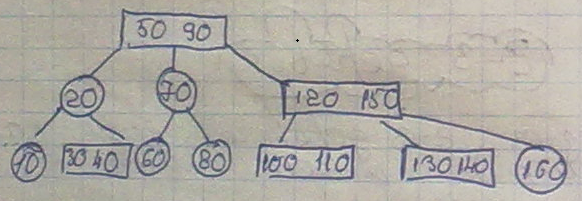
2-3 дерево поиска.
Ключи размещаются в соответствии со следующими правилами:
1 Двухместный внутренний узел имеет двух сыновей. Ключ двухместного узла должен быть больше, чем ключи левого поддерева и меньше, чем ключи правого поддерева.
2 Трехместный узел имеет трех сыновей. Должен содержать два элемента данных. Ключ S больше TL, но меньше TM, а ключ L больше, чем TM, но меньше TR.
3 Лист может содержать один или два элемента данных.
34 Обход 2-3 дерева.
Node2-3Tree = (S, L, Left, Middle, Right)
Обход:
Алгоритм InOrder(R)
1 if (R-лист) then
2 Обрабатываем элементы в узле R
3 else if (R – трехместный) then
4 InOrder(R^.left)
5 Обработать первый элемент
6 InOrder(R^.middle)
7 Обработать второй элемент
8 InOrder(R^.right)
9 Обработать третий элемент
10 InOrder(R^.left)
11 Обработать элемент узла
12 InOrder(R^.right)
13 end if
14 end if
Поиск:
Алгоритм Retrieve(R, key, elem)
1 if (keyR) then
2 elem данные, содержащиеся в узле R
3 return true
4 else
5 if (R – лист) then return false
6 else if (R – трехместный) then
7 if (key < R.S) then
return Retrieve(R^.left, key, elem)
8 else if ( key < R.L) then
return Retrieve (R^.middle, key, elem)
9 else return Retrieve (R^.right, key, elem)
10 end if
11 end if
12 else
13 if (key < R.S) then
14 return Retrieve(R^.left, key, elem)
15 else return Retrieve (R^.right, key, elem)
16 end if
17 end if
18 end if
35 Добавление элемента в 2 – 3 дерево.
Алгоритм вставки:
1 Нужно найти лист, на котором прекращается поиск этого элемента
2 Вставить элемент в этот узел. Если после вставки лист содержит 3 элемента – выполнить разделение:
Разделение внутреннего узла:
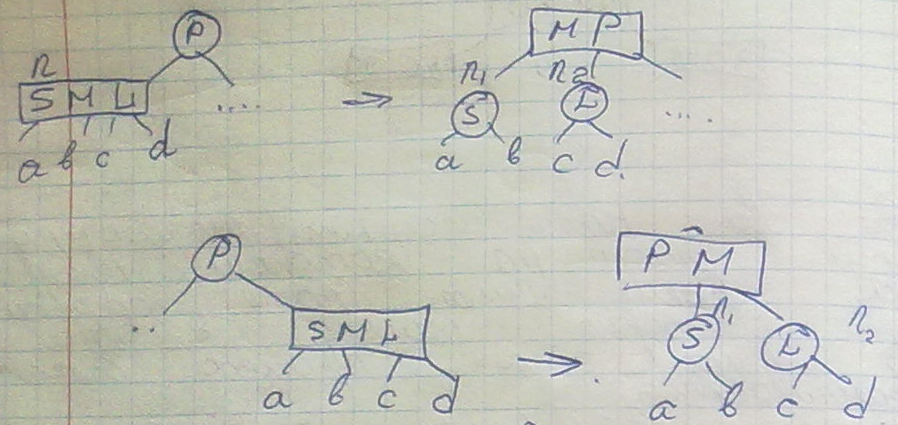
Разделение корня:
Алгоритм Insert (R, newelem)
1 присвоить key ключ newelem
2 найти лист leafnode, но который можно разместить ключ key
3 добавить элемент newelem в лист leafnode newelem
4 if (leafnode содержит три элемента) then
Split (leafnode)
Алгоритм Split(n)
1 if (n – корень) then
2 создать новый узел p
3 назначить узел p родителем n
4 end if
5 создать два новых узла n1, n2 и назначить их родителем узел p
6 в узел n1 записать меньший ключ из n
7 в узел n2 записать больший ключ из n
8 if (n – не является листом) then
9 n1 – родитель двух левых сыновей n
10 n2 – родитель двух правых сыновей n
11 end if
12 перенести средний ключ в узел p
13 if (p содержит 3 элемента) then
Split(p)
Эффективность – О(log(n))
36 Удаление элемента в 2 – 3 дереве.
При удалении ключа из узла возникают три варианта.
1) Если после удаления ключа в узле содержится два ключа, то после удаления ничего не меняется.
2) Если же у ключа после удаления остался один элемент, то проверяем количество потомков второго ребенка того узла, ребенком которого является узел с удаляемым ключом. Если у него два ребенка, то присваиваем ему оставшийся один элемент. Вершину, оставшуюся без детей, удаляем рекурсивно.
3) Иначе у него три ребенка. Тогда присваиваем узлу с одним ключом один из этих ключей, таким образом получая два узла с двумя ключами.
Алгоритм удаления Delete(r, key)
1 Найти позицию элемента key
2 if (elem – не лист) then
3 Поменять местами найденный элемент с симметричным приемником
4 end if
5 удаляем элемент elem из leafnode
6 if (leafnode – пуст) then Fix(leafnode)
Алгоритм Fix(n)
1 if (n – корень) then
2 удалить корень
3 else
4 установить p на родительский узел узла n
5 if (брат узла n содержит два элемента) then
6 выполнить перераспределение между n, братом и p
7 if (n – внутренний) then
8 переместить соответствующий доч. узел от брата к n
9 end if
10 else
11 установить s на брата n
12 перенести из p в s
13 if (n – внутренний) then
14 присоединить доч. узел узла n к s
15 end if
16 удалить n
17 if (p – пуст) then Fix(p)
18 end if
19 end if