62. Нахождение кратчайших путей в графе. Алгоритм Форда – Беллмана

Будем рассматривать ориентированные графы G = <V, Е>, дугам которых приписаны веса. Это означает, что каждой дуге (u, v)E поставлено в соответствие некоторое вещественное число a(u, v), называемое весом данной дуги. Полагаем, что a(u, v)=, если не существует дуга (u, v). Если последовательность вершин Vq , V1,..., V_p определяет путь в графе G, то его длина определяется как сумма . Нас будет интересовать нахождение кратчайшего пути между двумя фиксированными вершинами s, t V. Длину такого пути обозначим d(s, t) и назовем расстоянием от s до t (расстояние, определенное таким образом, может быть и отрицательным). Если не существует ни одного пути из s в t, то полагаем d(s, t) =. Отметим, что если каждый контур нашего графа имеет положительную длину, то кратчайший путь будет всегда элементарным путем.

Для произвольных s, t V (st) существует вершина v такая, что d(s, t) = d(s, v) + d(v, t).

Таким свойством обладают предпоследние вершины кратчайшего пути из s в t. Далее мы можем найти вершину и, для которой d(s, v) = d(s, u) + d(u, v) и т.д. Из условия положительности длины всех контуров следу­ет, что последовательность t, v, u, ... не содержит повторений и заканчивается вершиной s. Перечислив верши­ны в обратном порядке, найдем кратчайший путь из s в t.

Алгоритм для нахождения кратчайшего пути можно построить с использованием стека, куда последова­тельно заносим вершины t, v,u, ..., s:

1 BEGIN

2. СТЕК :=; СТЕК  t; v := t;

3. WHILE vs DO

4. BEGIN

5. u := вершина, для которой d[v] = d[u] + a[u, v]

6. СТЕК  u;

7. v := u

8 END

9 END

Отметим, что если выбор вершины и в строке 5 происходит в результате просмотра всех вершин, то слож­ность нашего алгоритма - 0(n²). Если же будем просматривать только список ПРЕДШ[у], содержащий все вершины и, такие, что u—>v, то сложность будет О(m).

Алгоритм Форда-Беллмана.O(n³) При данной матрице весов дуг a[u, v], u, ve V, вычисляем некоторые верхние ограничения d[v] на расстоя­ния от вершины s до всех v е V.

Каждый раз, когда окажется, что D[u]+a[u, v]<D[v] (1), оценку D[v] улучшаем: D[v] := D[u]+a[u, v]. Про­цесс прерывается, когда дальнейшее улучшение ни одного из ограничений невозможно. Легко показать, что значение каждой из переменных D[v] в этом случае равно кратчайшему пути от s к v.

Таким образом для вычисления расстояния от s до t мы находим расстояние от s до всех вершин графа. Алгоритм Belman-Ford(G,A,S,t)1.for each vV do d[v] 2.d[S]<- 0; 3.for k=1 to n-1 do 4.for each vV-{S} do 5.for each wV do if d[v]>d[w]+a[w,v] then d[v] d[w]+a[w,v] end for;end for; end for.

63 Поиск кратчайших путей в графе. Алгоритм Дэйкстры.

Общая теория:

У нас есть граф G=(V,E), где связь между вершинами v и w следующая: a(v,w) E. Если связь между вершинами отсутствует, то a(v,w)=.

Если последняя вершина w_o, w₁, …, w_n определяет путь в графе, то его длина равна суммарному весу входящих вершин:

Наша задача – нахождение кратчайшего пути между вершинами S, t. M(S,t) – расстояние между S и t.

Путь из S в t, который имеет минимальную длину – есть кратчайший путь, между вершинами S и t.

d(S,t)=d(S,v_k) + a(v_k,t)

d(S,v_k)=d(S,v_k-1)+a(v_k-1,v_k)

v_k-1 v_k

t

S

Алгоритм Дейкстры позволяет найти путь с не отрицательными весами.

Алгоритм Dijkstra (G,A,S)

1. for each v V do d[v];

2. d[s]0; //путь до вершины S

3. S; //множество вершин с известным расстоянием

4. tv; //множество вершин с не известным расстоянем

5. while T0 do;

6. d[w]=min {d[p], p T};

7. SSV{w}; TT-{w};

8. for each v T do;

9. if d[v] > d[w]+a[w,v] then;

10. d[v] d[w] + a[w,v];

11. end for;

12. end while;

13. return d.

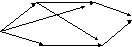# A 3 B 2

4 9 E

S 2 2

3

C 3 D

d[S]=0; d[A]=; d[B]=; d[C]=; d[D]=; d[E]=;

S; T={S, A, B, C, D, E};

d[A]=min{d[A], d[S] + a[S,A]=4};

d[B]=min{d[B], d[S] + a[S,B]=9};

d[C]=3; – Минимальное значение переносим во множество S;

d[D]=;

d[E]=;

S={S,C} T={A,B,D,E};

Пересчитываем

d[A]=min{d[A], d[C] + a[C,A]}=min{4, 3 + } = 4;

d[B]=min{d[B], d[C] + a[C,B]}=min{9, 3 + }=9;

d[D]=min{d[D], d[C] + a[C,D]}=min{, 3 + 3}=6;

d[E] =;

S={S,C,A} T={B,D,E};

Пересчитываем

d[B]=min{d[B], d[А] + a[А,B]}=min{9, 3 + 4}=7;

d[D]=min{d[D], d[А] + a[А,D]}=min{6, 4 + 2}=6;

d[E] =;

S={S,C,A,D} T={B,E};

Пересчитываем

d[B]=min{d[B], d[D] + a[D,B]}=min{7, 6 + }=7;

d[E] = min{d[E], d[D] + a[D,E]}=8;

S={S,C,A,D,B} T={E};

Пересчитываем

d[E] = min{d[E], d[B] + a[B,E]}=min{9,8}=8;

S={S,C,A,D,B,E} T=;