Г л а в а 4 дискретизация и квантование непрерывных сообщений

4.1. Основные понятия и определения

Переход от аналогового представления сигнала к цифровому, который дает в ряде случаев значительные преимущества при передаче, хранении и обработке информации, связан с дискретизацией сигнала х(t) по времени и с квантованием по уровню.

Рассмотрим разновидности сигналов, которые описываются функцией х(t).

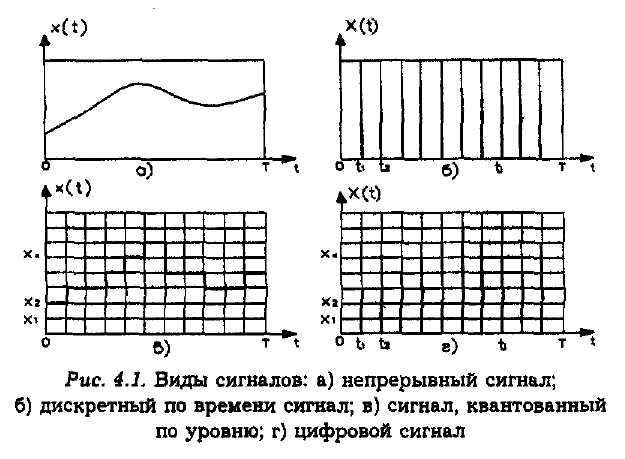Рис. 4.1. Виды сигналов: а) непрерывный сигнал;

б) дискретный по времени сигнал; в) сигнал, квантованный по уровню;

г) цифровой сигнал

Непрерывная функция непрерывного аргумента (непрерывный сигнал, рис. 4.1а). В этом случае значения, которые может принимать функция x(t)и аргумент t, заполняют конечные (или бесконечные) промежутки [0, X] и [0, T] соответственно.

Непрерывная функция дискретного аргумента (дискретный во времени сигнал, рис. 4.1б). Здесь значения функции x(t) определяются лишь на дискретном множестве значений аргумента t_i,i=0, 1, 2, …, (0<t<T).

Дискретная функция непрерывного аргумента (квантованный по уровню сигнал, рис. 4.1в). В этом случае значения, которые может принимать функция x(t), образуют дискретный ряд чисел x₁,x₂, …,x_k, …, т.е. такой конечный или бесконечный ряд, в котором каждому числу можно поставить в соответствие интервал (a_k,b_k), внутри которого других чисел данного ряда нет. Значение аргумента t может быть любым на отрезке [0, T].

Дискретная функция дискретного аргумента (цифровой сигнал, рис. 4.1г). Значения, которые могут принимать функция x(t) и аргумент t, образуют дискретные ряды чисел x₁,x₂, …,x_k, … и t₀,t₁,t₂, …,t_i, …, заполняющие отрезки [0, X] и [0, T]соответственно.

Дискретизация состоит в преобразовании сигнала x(t) непрерывного аргумента tв сигнал x(t_i) дискретного аргумента t_i.

Квантование по уровню состоит в преобразовании непрерывного множества значений сигнала x(t_i) в дискретное множество значений x_k,k=0, 1, 2, …,m-1.

Совместное применение операций дискретизации и квантования позволяет преобразовать непрерывный сигнал x(t) в дискретный по координатам x и t.

Применительно к детерминированной функции рассмотрим сущность понятия дискретизации сигнала x(t).

Дискретизация реализации сигнала x(t) связана с заменой промежутка изменения независимой переменной некоторым множеством точек, т.е. операции дискретизации соответствует выражение:

x(t)  x(t_i), (4.1)

где x(t) – функция, описывающая сигнал;

x(t_i) – функция, описывающая сигнал в результате дискретизации.

Следовательно, в результате дискретизации исходная функция x(t)заменяется совокупностью отдельных значений x(t_i).

По значениям функции x(t_i) можно восстановить исходную функцию x(t) с некоторой погрешностью. Функцию, полученную по результатам восстановления (интерполяции) по значениям x(t), будем называть воспроизводящей и обозначим через V(t).

Воспроизводящая функция V(t) строится как взвешенная сумма некоторого ряда функций f(t–t_k):

V(t) =  a_kf(t – t_k), (4.2)

k

причем коэффициенты a_kзависят от отсчетов x(t_i),x(t_i-1), …

При обработке сигналов дискретизация по времени должна производиться таким образом, чтобы по отсчетным значениям x(t_i) можно было получить воспроизводящую функцию V(t), которая с заданной точностью отображает исходную функцию x(t).

При дискретизации сигналов приходится решать вопрос о том, как часто следует производить отсчеты функции, т.е. каков должен быть шаг дискретизации t_i=t_i–t_i-1.

При малых шагах дискретизации t_i количество отсчетов функции на отрезке обработки будет большим и точность произведения – высокой. При больших t_iколичество отсчетов уменьшится, но при этом, как правило, снижается точность восстановления.

Оптимальной является такая дискретизация, которая обеспечивает представление исходного сигнала с заданной точностью при минимальном количестве выборок. В этом случае все отсчеты существенны для восстановления исходного сигнала. При неоптимальной дискретизации кроме существенных отсчетов имеются и избыточные отсчеты.

Избыточные отсчеты не нужны для восстановления сигнала с заданной точностью. Они загружают тракт передачи информации, отрицательно сказываются на производительности обработки данных ЭВМ, вызывают дополнительные расходы на хранение и регистрацию данных. В связи с этим актуальна задача сокращения избыточности данных. Сокращение избыточности для получателя информации может производиться в процессе дискретизации сигналов. В более общем плане задача сокращения избыточных отсчетов может рассматриваться как задача описания непрерывных сигналов с заданной точностью минимальным числом дискретных характеристик.