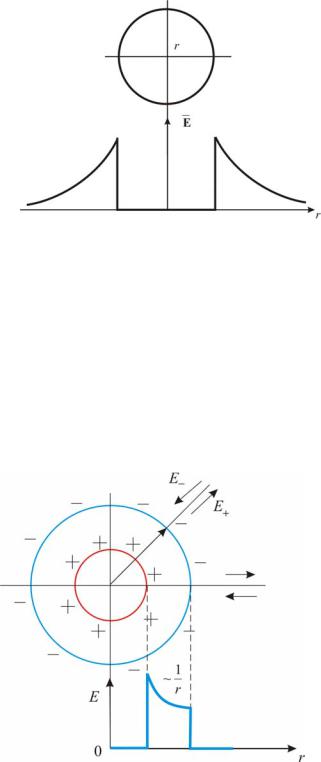
Рис. 2.14
2.5.4. Поле двух коаксиальных цилиндров с одинаковой линейной плотностью λ, но разным знаком.
Внутри меньшего и вне большего цилиндров поле будет отсутствовать Е = 0. В
зазоре между цилиндрами, поле определяется формулой:
E(r) = |
λ |
(2.5.8) |
|
2πε0 r |
|||
|
|
Это справедливо и для цилиндров конечной длины, если зазор между цилиндрами намного больше длины цилиндров (цилиндрический конденсатор).
Графически вышесказанное можно изобразить на рисунке 2.15.
Рис. 2.15
2.5.5. Поле заряженного пустотелого шара.
Пустотелый шар радиуса R, заряжен положительным зарядом с поверхностной r
плотностью σ. Поле в данном случае будет центрально симметричным, E – в любой точке проходит через центр шара. Еn = Е(r) и перпендикулярна поверхности в любой точке. Вообразим вокруг – сферу радиуса r (Рис. 2.16).
22
Рис. 2.16
Если r ≥ R, то внутрь попадет весь заряд q, распределенный по сфере
Е(r)4πr 2 = |
q |
(2.5.9) |
|||
ε0 |
|||||
откуда |
|
|
|||
q |
|
|
|
||
E(r) = |
|
|
(2.5.10) |
||
4πε0r2 |
|
||||
Если r < R, то Е(r) = 0.
Вне сферы поле тождественно полю точечного заряда той же величины, помещенному в центр сферы.
2.5.6. Поле объемного заряженного шара.
Как вы помните ρ – объемная плотность заряда. |
|
|||||||
ρ = |
q |
или ρ = |
|
q |
|
– для шара. |
(2.5.11) |
|
|
4 / 3πR3 |
|||||||
V |
|
|
|
|
||||
Для поля вне шара радиусом R (Рис. 2.17) получается тот же результат, что и для |
||||||||
пустотелой сферы, т.е. справедлива формула: |
|
|
|
|||||
|
|
E(r) = |
q |
|
|
(2.5.12) |
||
|
|
4πε0 r 2 |
|
|||||
Рис. 2.17
23
Но при r < R, сферическая поверхность будет содержать в себе заряд, равный
q = ρ |
4 |
πr3 , |
(2.5.13) |
|
3 |
|
|
где ρ – объемная плотность, 43 πr3 – объем.
Тогда по теореме Гаусса запишем:
Е(r) 4πr2 = 1 ρ 4 πr3
ε0 3
т.е. внутри шара
E(r) = ρr , 3ε0
Таким образом, внутри шара Е ~ r.
(2.5.14)
(2.5.15)
24
Тема 3. ПОТЕНЦИАЛ И РАБОТА ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ. СВЯЗЬ НАПРЯЖЕННОСТИ С ПОТЕНЦИАЛОМ.
3.1. Теорема о циркуляции вектора E .
3.2. Работа сил электростатического поля. Потенциальная энергия. 3.3. Потенциал. Разность потенциалов.
3.4. Связь между напряженностью и потенциалом.
3.5. Силовые линии и эквипотенциальные поверхности.
3.6. Расчет потенциалов простейших электростатических полей.
3.1. Теорема о циркуляции вектора E .
На прошлой лекции мы с вами говорили о том, что взаимодействие между покоящимися зарядами осуществляется через электростатическое поле. Описание
электростатического поля мы рассматривали с помощью вектора напряженности E , численно равного силе, действующей в данной точке на помещенный в нее пробный единичный положительный заряд.
Er = F
qпр.
Существует, однако, и другой способ описания – с помощью потенциала.
Однако для этого необходимо сначала доказать, что силы электростатического поля
консервативны, а само поле потенциально.
Рассмотрим поле, создаваемое неподвижным точечным зарядом q. В любой точке этого поля на пробный точечный заряд q' действует сила F (Рис. 3.1).
Рис. 3.1
r |
1 |
|
qq' r |
r |
||
F = |
|
|
|
lr = F(r)lr |
||
4πε0 |
ε r 2 |
|||||
|
|
|
||||
где F(r) – модуль вектора силы |
F , |
lr – орт |
радиуса-вектора r , определяющая |
|||
положение заряда q' относительно q, ε – электрическая постоянная, ε0 – относительная диэлектрическая проницаемость среды.
25
Для того чтобы доказать, что электростатическое поле потенциально, нужно доказать, что силы электростатического поля консервативны. Из механики известно,
что любое стационарное поле центральных сил является консервативным, т.е. работа сил этого поля не зависит от формы пути, а только от положения конечной и начальной точек.
Вычислим работу, которую совершает электростатическое поле созданное зарядом q по перемещению заряда q' из точки 1 в точку 2.
Работа на пути dl равна
dA = Fdlcosα = 4πεε1 0 qqr 2 ' dlcosα
dr – приращение радиус-вектора r при перемещении на dl; dr = dl·cosα, т. е.
dA = |
qq' |
dr |
|
4πεε0 r 2 |
|||
|
|
Тогда полная работа при перемещении q' из точки 1 в точку 2 равна интегралу:
|
|
qq' r2 |
dr |
|
qq' |
|
|
|
1 |
r2 |
|
qq' |
|
|
1 |
|
1 |
|
|||
A |
= |
|
|
|
|
= |
|
|
|
− |
|
|
|
= |
|
|
|
|
− |
|
|
4πεε |
|
∫r 2 |
4πεε |
|
r |
r |
4πεε |
|
|
r |
|||||||||||
12 |
|
0 |
|
0 |
|
|
|
|
0 |
r |
|
|
|||||||||
|
|
|
r |
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
2 |
|
|||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.1.1)
(3.1.2)
(3.1.3)
Получим, что работа электростатических сил не зависит от формы пути, а только лишь от координат начальной и конечной точек перемещения. Следовательно,
силы поля консервативны, а само поле – потенциально.
Этот вывод можно распространить и на поле, созданное системой зарядов. Это следует из принципа суперпозиции полей: E=ΣEi – напряженность поля системы зарядов равна сумме напряженностей полей, которые создавал бы каждый из зарядов системы в отдельности, мы его рассмотрели раньше.
Итак, как и в механике любое стационарное поле центральных сил является консервативными, т.е. работа сил этого поля не зависит от формы пути, а только от положения начальной и конечной точек. Именно таким свойством обладает электростатическое поле – поле, образованное системой неподвижных зарядов. Если в
качестве, пробного заряда, перенесенного из точки 1 (Рис. 3.2) заданного поля E в точку 2 взять единичный положительный заряд, то элементарная работа сил поля будет равна:
dA = Edl |
(3.1.4) |
Рис. 3.2
А вся работа равна:
2 |
r r |
|
A = ∫Edl |
(3.1.5) |
|
1 |
|
|
Такой интеграл по замкнутому контуру называется циркуляцией вектора E .
Из независимости линейного интеграла от пути между двумя точками следует,
что по произвольному замкнутому пути: |
|
∫Edl = 0 |
(3.1.6) |
Это утверждение и называют теоремой о циркуляции E .
26
Для доказательства теоремы разобьем произвольно замкнутый путь на две части: 1а2 и 2b1 (Рис. 3.2). Из сказанного выше следует, что
∫2 Edl = −∫1 Edl
1 |
2 |
(Интегралы по модулю равны, но знаки противоположны) поэтому:
r r |
2 |
r r |
1 |
r r |
|
|
q∫Edl |
= q∫Edl |
−q∫Edl |
= 0 |
(3.1.7) |
||
|
1 |
|
2 |
|
|
|
Поле, обладающее такими свойствами, называется потенциальным. Любое электростатическое поле является потенциальным.
Теорема о циркуляции позволяет сделать ряд важных выводов, практически не прибегая к расчетам:
Два примера:
1. Линии электростатического поля не могут быть замкнутыми. В самом
деле, если это не так, и какая-то линия E – замкнута, то, взяв циркуляцию вдоль этой линии, мы сразу же придем к противоречию с теоремой о циркуляции
вектора E . 
∫Edl = 0 . А в данном случае направление интегрирования в одну
сторону – поэтому циркуляция вектора E не равна нулю.
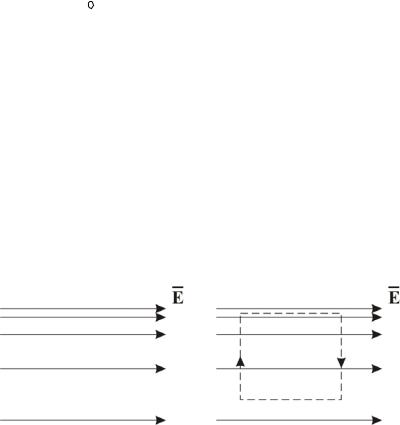
2. Возможна ли конфигурация электростатического поля как на рисунке
3.3?
Рис. 3.3
Нет невозможна! Применим теорему о циркуляции вектора E к замкнутому контуру, показанному пунктиром. Стрелки здесь показывают направление обхода.
На вертикальных участках E перпендикулярно dl и Edl = 0 . Остаются два одинаковых по длине горизонтальных участка. Из рисунка видно, что вклады в циркуляцию на этих участках противоположны по знаку, но не равны по модулю:
E больше там, где линии гуще, поэтому циркуляция отлична от нуля, что противоречит теореме о циркуляции.
3.2. Работа сил электростатического поля. Потенциальная энергия.
До сих пор мы рассматривали описание электрического поля с помощью вектора
напряженности E . Другой способ описания поля – с помощью потенциала.
Мы сделали заключение, что электростатическое поле потенциально. Следовательно, можно ввести функцию состояния зависящую от координат –
потенциальную энергию. Раньше мы показали, что
E = ∑Ei , тогда qE = q∑Ei |
|
F = ∑Fi |
(3.2.1) |
27