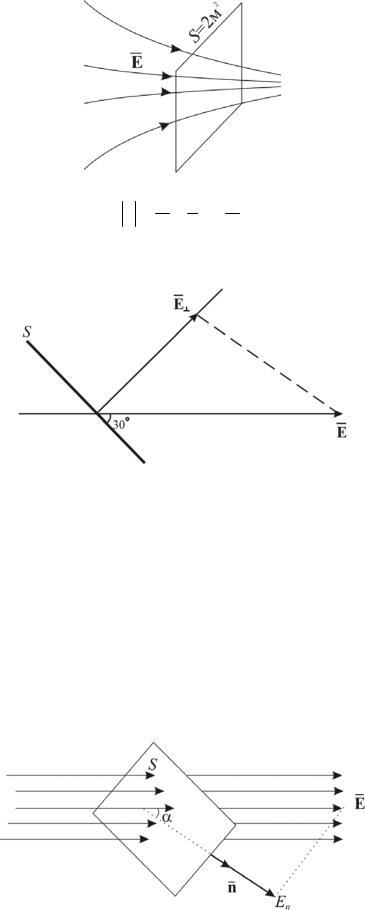
Рис. 2.3
Er = ФS = 42 = 2 Bм .
Пример 2: площадка S = 3м2 находится в однородном поле 100 Н/Кл. Сколько линий пересекает эту площадку, если угол составляет 30º (Рис. 2.4).
Рис. 2.4
Е┴= Е sin 300= 50 Н/Кл
Ф= Е┴·S = 50·3=150 линий
2.2.Поток вектора напряженности.
Итак, на примерах мы показали, что если силовые линии однородного
электрического поля напряженностью E пронизывают некоторую площадку S, то поток напряженности (раньше мы называли число силовых линий через площадку) будет определяться формулой
Фr E = ES = ES cos α = En S ,
где En – произведение вектора E на нормаль n к данной площадке (Рис. 2.5).
Рис. 2.5
14
А величина ФЕ здесь и называется потоком вектора напряженности электрического поля через площадку S, т.е. определение:
Полное число силовых линий, проходящих через поверхность S называется потоком вектора напряженности ФЕ через эту поверхность.
В векторной форме можно записать
r |
ФЕ = ( Е,S ) – скалярное произведение двух векторов, |
||
r |
|
||
где вектор S = nS . |
r |
||
Т.е. поток вектора |
|||
E есть скаляр, который в зависимости от величины угла α |
|||
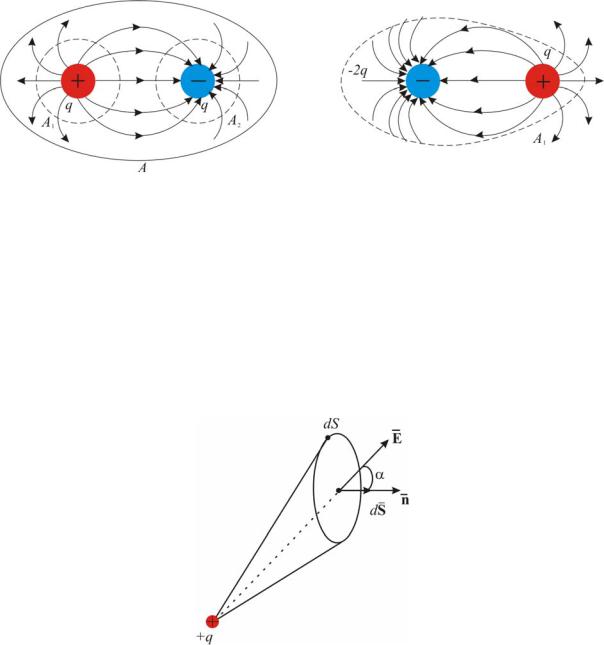
может быть как положительным, так и отрицательным. Рассмотрим (Рис. 2.6, 2.7).
Для этой конфигурации поток через поверхность А, отрицательный (подсчитайте число силовых линий).
Рис. 2.6 Рис. 2.7
Для рисунка 2.6 – поверхность А1 окружает положительный заряд и поток здесь направлен наружу, т.е. ФЕ > 0. Поверхность А2 – окружает отрицательный заряд и здесь ФЕ < 0 направлен внутрь.
Для рисунка 2.7 – поток будет не равно нулю если суммарный заряд внутри поверхности не равен нулю. Т.е. поток зависит от заряда. В этом смысл теоремы Гаусса.
2.3. Теорема Остроградского-Гаусса.
Итак, вспомним поток вектора напряженности электрического поля – равен числу линий напряженности, проходящей через площадь S (Рис. 2.8).
Рис. 2.8 |
|
dФЕ = ЕdS cosα = En dS |
(2.3.1) |
15
Т.е. в однородном поле ФЕ=ЕS в произвольном электрическом поле
|
ФЕ = ∫ЕndS = ∫EdS |
(2.3.2) |
|
|
S |
S |
|
|
dSr = dSnr – в векторной форме |
|
|
r |
Ориентация dS в пространстве задается с помощью единичного вектора nr . Т.е. |
||
dS |
– направление совпадает с направлением внешней нормали к поверхности. |
||
|
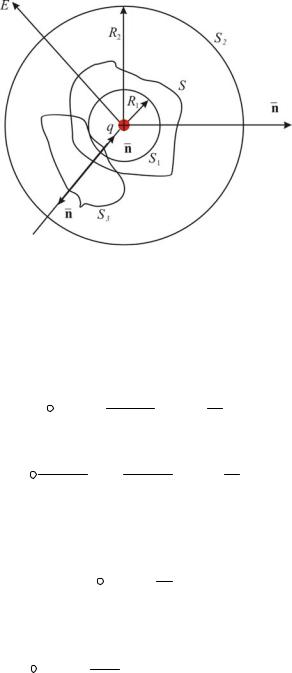
Подсчитаем поток вектора E через |
замкнутую поверхность |
S, окружающую |
точечный заряд q (Рис. 2.9.).
Рис. 2.9
Центр окружности совпадает с центром заряда. Радиус сферы S1 равен R1. В
каждой точке поверхности S1 проекция E на направление внешней нормали одинакова и равна
En = |
1 |
|
|
q |
|
(2.3.3) |
||
4πε |
0 |
|
R |
2 |
|
|
||
|
|
|
|
|
|
|||
Тогда поток через S1 |
|
1 |
|
|
|
|||
q |
|
|
|
|
q |
|
||
ФE = ∫EndS = |
|
2 4πR12 = |
(2.3.4) |
|||||
S |
4πε0 R1 |
|
|
ε0 |
|
|||
1 |
|
|
|
|
|
|
|
|
Подсчитаем поток через S2 (радиус
ФЕ = ∫4πεq R2 dS =
S2 r0 2
Линии напряженности E начинаются и заканчиваются на бесконечности) из непрерывности линии Е следует, что поток произвольную поверхность S будет равен этой же величине:
ФЕ = ∫ЕndS = |
q |
S |
ε0 |
|
(2.3.5) |
зарядах |
(или в |
и через |
любую |
|
(2.3.6) |
Полученный результат справедлив не только для одного заряда, но и для любого числа произвольно расположенных зарядов, находящихся внутри поверхности
ФЕ = ∫ЕndS = |
∑q |
– теорема Гаусса |
(2.3.7) |
|
ε0 |
||||
S |
|
|
Поток вектора напряженности электрического поля через замкнутую поверхность в вакууме равен алгебраической сумме всех зарядов, расположенных внутри поверхности, деленной на ε0.
16
При вычислении потока через замкнутую поверхность, вектор нормали n
следует считать направленным наружу! Линии E выходящие из объема,
ограниченного данной поверхностью создают положительный поток, линии же входящие в объем – отрицательный поток.
Если между нашими сферами расположить ещё одну поверхность S3, не
охватывающую заряд, то, как видно из (Рис. 2.9). Каждая линия напряженности E, будет дважды пересекать эту поверхность: один раз с положительной стороны – войдет
вповерхность S3, другой раз – с отрицательной стороны – выйдет из поверхности S3.
Врезультате алгебраическая сумма линий напряженности, проходящая через
замкнутую поверхность S3 будет равна нулю, т.е. полный поток проходящий через S3, равен нулю.
Таким образом для точечного заряда q, полный поток через любую замкнутую поверхность S будет равен:
Ф |
= |
q |
- если заряд расположен внутри замкнутой поверхности. |
Е |
|
ε |
|
|
|
0 |
|
ФЕ = 0 – если заряд расположен вне замкнутой поверхности и этот результат
не зависит от формы поверхности и знак потока совпадает со знаком заряда.
В общем случае электрические заряды могут быть «размазаны» с некоторой объемной плотностью ρ различной в разных местах пространства. Вспомним ещё одно понятие – объемная плотность заряда
ρ = |
q |
или |
dq |
, |
(2.3.8) |
|
dV |
||||
V |
|
|
|
||
где dV- бесконечно малый объем.
Под физически бесконечно малым объемом dV следует понимать такой объем, который с одной стороны достаточно мал, чтобы в пределах его плотность заряда считать одинаковой, а с другой – достаточно велик, чтобы не могла проявиться дискретность заряда, т.е. то, что любой заряд кратен целому числу элементарных зарядов e или P+ (протон). Тогда суммарный заряд
∑qi = ∫ρdV |
|
(2.3.9) |
|
|
V |
|
|
Тогда из теоремы Гаусса (2.3.7.) пишем |
|
|
|
r |
r |
|
|
|
1 |
ρdV |
(2.3.10) |
S |
ε0 V∫ |
|
|
- это ещё одна форма записи теоремы Гаусса, если заряд непрерывен.
Необходимо обратить внимание на следующее обстоятельство: в то время, как r
само поле E зависит от конфигурации всех зарядов, поток ФE сквозь произвольную замкнутую поверхность определяется только алгебраической суммой зарядов внутри поверхности S. Это значит, что если передвинуть заряды, то E изменится всюду, и на поверхности S, а вот поток вектора E через эту поверхность останется прежним. Удивительное свойство вектора напряженности E.
2.4.Дифференциальная форма теоремы Гаусса.
Вней установлена связь между объемной плотностью заряда ρ и изменением E в окрестности данной точки пространства
17