Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

МИРЭА - Российский технологический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Краткий курс математического анализа. Том 2

.pdf

Скачиваний:

383

Добавлен:

10.05.2015

Размер:

4.49 Mб

Скачать

☆

<<< < Предыдущая 17 18 19 20 21 22 23 24 25 26 27 2829 / 4729 30 31 32 33 34 35 36 37 38 39 40 41 > Следующая >>>

280 Гл. 6. Гармонический анализ

Поэтому функция f и функция f , рассматриваемая только на отрезке

[−π, π], имеют один и тот же ряд Фурье.
	З а м е ч а н и е 5. Если функция		f является		T -периодической,
		интегрируемой		на отрезке [0, T ] (в соб-
		ственном	или	несобственном смысле),
		ственном	или	несобственном смысле),
		то для любого числа a имеет место равен-
		ство (рис. 64)
		a+T			T
			f (x) dx =		f (x) dx.
			f (x) dx =		f (x) dx.
			a		0

В частности, для коэффициентов Фурье 2π-периодической функции, абсолютно интегрируемой на отрезке [−π, π], справедливы формулы

				1	2π
		a0	=	1			f (x) dx,
		a0	=	2π			f (x) dx,
				2π
					0
	1	2π			1		2π
an =	1	f (x) cos nx dx,	bn =		1		f (x) sin nx dx, n = 1, 2, ... .
an =	π	f (x) cos nx dx,	bn =			π	f (x) sin nx dx, n = 1, 2, ... .
	π					π
		0					0

51.2. Приближение функций ступенчатыми функциями.

Для изучения сходимости рядов Фурье полезно предварительно рассмотреть способ приближения абсолютно интегрируемых функций так называемыми ступенчатыми функциями (их определение будет дано ниже).

О п р е д е л е н и е 2. Пусть на множестве X Rn задана функ-

ция f. Замыкание множества всех точек x X, в которых функция f не равна 0, называется носителем функции f и обозначается supp f 1):

supp f = {x X : f (x) = 0}.

О п р е д е л е н и е 3. Если у функции f , определенной на всем пространстве Rn, ее носителем является компакт, лежащий в открытом множестве G (в частности, на интервале (a, b) числовой прямой R), то f называется финитной на множестве G функцией (соответственно финитной на интервале (a, b) функцией).

Если функция финитна на пространстве Rn (в частности, на R), то для краткости будем называть ее финитной, опуская указание, где

именно она финитна.

1) От латинского слова supportus — опора.

§ 51. Тригонометрические ряды Фурье

281

Если функция f финитна на интервале (a, b), т. е. supp f (a, b), то множество supp f является компактом, а следовательно, замкнутым множеством, лежащим на интервале (a, b). Поскольку точки a и b ему не принадлежат, то они не являются его точками прикосновения. Поэтому у них существуют окрестности, не со-

держащие точек множества supp f. Во всех

точках этих окрестностей функция f , очевидно, равна нулю (рис. 65).

О п р е д е л е н и е 4. Для всякого множе-

ства X Rn функция, равная 1 в точках этого

множества и равная 0 вне его, называется характеристической функцией множества X и обозначается χX (x).

Таким образом,

1, если x X,

χX (x) = 0, если x X.

В дальнейшем в этом параграфе мы будем рассматривать только функции одной переменной.

О п р е д е л е н и е 5. Всякая линейная комбинация конечного

множества характеристических функций попарно непересекающихся конечных полуинтервалов вида [a, b) называется ступенчатой функцией.

Таким образом, если ϕ — ступенчатая функция, то существуют такая конечная система попарно непересекающихся конечных полуинтервалов [aj , bj ) и такие числа αj , j = 1, 2, ..., k, что

k
j
ϕ(x) = αj χj (x),	(51.7)
=1

где χj — характеристическая функция полуинтервала [aj , bj ). Очевидно, что ступенчатая функция является финитной функ-

цией, ибо замыкание объединения конечного множества конечных промежутков является компактом.

З а м е ч а н и е 1. Ступенчатая функция интегрируема на всей числовой оси, причем, если она задана формулой (51.7), то

+∞	k	+∞	k	bj	k
ϕ(x) dx =	αj	χj (x) dx =	αj	dx =	αj (bj − aj ).
−∞	=1	−∞	j=1		j=1
−∞	j	−∞	aj

(51.8)

Те о р е м а 2. Если функция f абсолютно интегрируема на конечном или бесконечном промежутке с концами в точках a и b,

282	Гл. 6. Гармонический анализ

−∞ a < b +∞, то для любого ε > 0 существует такая ступенчатая функция ϕ с носителем в интервале (a, b):

что	supp ϕ (a, b),	(51.9)
что	b
	b
	\|f (x) − ϕ(x)\| dx < ε.	(51.10)

Пусть сначала функция f интегрируема по Риману на любом конечном отрезке [ξ, η] (a, b). Зададим произвольно ε > 0. В силу абсолютной интегрируемости функции f и согласно определению несобственного интеграла существуют такие точки ξ и η, что a < ξ < η < b и

ξ	b
	\|f (x)\| dx + \|f (x)\| dx <	ε	.	(51.11)
		2

aη

Пусть τ — некоторое разбиение отрезка [ξ, η], |τ | — его мелкость и sτ — нижняя сумма Дарбу функции f , соответствующая разбие-

нию τ ; тогда

lim sτ = f (x) dx.

|τ|→0

Отсюда в силу определения предела следует, что существует такое разбиение τ0 = {xi}ii==i00 отрезка [ξ, η], что

0 f (x) dx − sτ0 <

(51.12)

Положим

inf f (x),

= x

i −

i−1

, i = 1, 2,

;

(51.13)

[xi−1,xi ]

...

тогда

sτ0 =

mi xi =

mi(xi − xi−1).

(51.14)

i=1

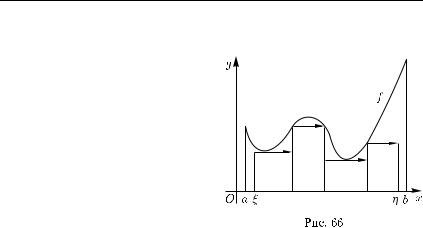
Это выражение напоминает формулу для значения интеграла от ступенчатой функции (51.8). Построим соответствующую ступенчатую функцию. Положим

def	mi,	если	xi−1 x < xi,	(51.15)
ϕ(x) =			i = 1, 2, ..., i0,	(51.15)
		если	x < ξ или x η
	0,	если	x < ξ или x η

	§ 51. Тригонометрические ряды Фурье			283
(рис. 66). Очевидно, что ϕ — ступенчатая финитная на интервале (a, b)
функция. Действительно, если χi — характеристическая функция
полуинтервала [xi−1, xi), то
	i0
ϕ(x) =	miχi(x);	(51.16)
	=1
i
при этом
supp ϕ [ξ, η] (a, b).		(51.17)
Сравнив	выражение	(51.14)
для суммы Дарбу sτ0 со зна-
чением интеграла от функции
(51.16) (см.(51.8)), убедимся, что
они равны:	η		i0
	η

	ϕ(x) dx =		mi(xi − xi−1) = sτ0 .	(51.18)
	ξ		=1
	ξ		i

Следовательно,

[f (x)

−

ϕ(x)] dx = f (x) dx

−

ϕ(x) dx =

f (x) dx − sτ0

(51.18)

(51.12)

(51.19)

Отметим, что при всех x [xi−1, xi), i = 1, 2, ..., i0,

выполняются

неравенства mi (51.13) f (x), поэтому ϕ(x)(51.15)f (x) для всех x [ξ, η) и

f (x) − ϕ(x) = |f (x) − ϕ(x)| 0.

(51.20)

Теперь из (51.11) и (51.19) имеем

|f (x) − ϕ(x)| dx (51.17)

f (x)

dx + f (x)

−

ϕ(x)

dx + f (x)

dx <

= ε.

(51.17)

(51.11)

(51.19)

(51.20)

В общем случае абсолютно интегрируемой функции, когда правильное разбиение {xi}ii==k0 промежутка интегрирования функции f (замечание 1 из п. 51.1) содержит точки, отличные от точек a и b, утверждение теоремы следует из того, что в силу доказанного оно справедливо для каждого промежутка с концами в точках xi−1 и xi этого разбиения, i = 1, 2, ..., k.

Положив ε = 1/n и обозначив соответствующую этому ε (в силу приведенной выше конструкции) ступенчатую функцию через

284	Гл. 6. Гармонический анализ

ϕn, получим такую последовательность таких ступенчатых функций {ϕn}, что

lim |f (x) − ϕn(x)| dx = 0, supp ϕn (a, b), n = 1, 2, ... (51.21)

n→∞

З а м е ч а н и е 2. Заметим, что из определения ступенчатой функции ϕ, построенной при доказательстве теоремы 2 (см. (51.15)), следует, что если для всех x [ξ, η] выполняется неравенство

			\|f (x)\| c,	(51.22)
то выполняется и неравенство
			\|ϕ(x)\| c.	(51.23)
Действительно, если	−c f (x) c,			то для любой точки x
[xi−1, xi], i = 1, 2, ..., i0,	будем иметь
c		m	inf
−			i = [xi−1,xi ] f (x) c.

Поэтому (см. (51.15)) для всех x [xi−1, xi) имеет место неравенство −c ϕ(x) c, т. е. |ϕ(x)| c на всех полуинтервалах [xi−1, xi),

аследовательно, и на отрезке [ξ, η] (заметим, что ϕ(η) = 0).

51.3.Теорема Римана. Стремление коэффициентов Фурье к нулю. Вернемся снова к изучению рядов Фурье абсолютно интегрируемых функций и покажем, что последовательность их коэффициентов Фурье стремится к нулю. Докажем даже более сильное

утверждение, принадлежащее Б. Риману.

Те о р е м а 3 (Риман). Если функция f абсолютно интегрируема на конечном или бесконечном промежутке с концами a и b, −∞a < b +∞, то

b	b
lim	f (x) cos λx dx = lim f (x) sin λx dx = 0.	(51.24)
λ→∞	λ→∞
a	a

С л е д с т в и е. Коэффициенты Фурье an и bn абсолютно интегрируемой на отрезке [−π, π] функции стремятся к нулю при n → ∞:

lim an =	lim bn = 0.	(51.25)
n→∞	n→∞

Доказательство теоремы разобьем на три этапа.

1. Если функция f является характеристической функцией χ по-

луинтервала [ξ, η) (a, b)

и λ = 0, то

|λ|

χ(x) cos λx dx

cos λx dx

sin λη − sin λξ

§ 51. Тригонометрические ряды Фурье

285

Отсюда	b
lim	χ(x) cos λx dx = 0.	(51.26)
λ→∞	a
Аналогично,	a
Аналогично,	b
lim	χ(x) sin λx dx = 0.	(51.27)
λ→∞	a
	a

2. Если функция f является ступенчатой функцией ϕ, носитель которой лежит на интервале (a, b), то она является конечной линейной комбинацией характеристических функций χi, i = 1, 2, ..., k, некото-

рых полуинтервалов [xi−1, xi), лежащих вместе со своими концами
в интервале (a, b):		k
		k
	ϕ(x) =		αiχi(x).
		=1
Следовательно,		i
Следовательно,
b	k		b
	k
lim ϕ(x) cos λx dx =	αi	lim	χi(x) cos λx dx = 0.	(51.28)
λ→∞	i=1	λ→∞	(51.26)
a			a
Аналогично,	b
lim	ϕ(x) sin λx dx = 0.			(51.29)
λ→∞			(51.27)
	a

3. Пусть f — произвольная абсолютно интегрируемая на промежутке с концами a и b функция. Зададим произвольно ε > 0. Согласно теореме 2 существует такая ступенчатая функция ϕ, что

b
\|f (x) − ϕ(x)\| dx <	ε	.	(51.30)
	2
a

В силу равенства (51.28) для этой функции ϕ существует такое λε, что для всех λ, удовлетворяющих неравенству |λ| > λε, выполняется

неравенство	b ϕ(x) cos λx dx	<	2ε .	(51.31)

Поскольку f (x) = [f (x) − ϕ(x)] + ϕ(x) и | cos λx| 1, то при |λ| > λε будем иметь

	b	b		b
		b	b

a f (x) cos λx dx		a	[f (x) − ϕ(x)] cos λx dx +	a	ϕ(x) cos λx dx

			ε		ε
\|f (x) − ϕ(x)\| dx +	ϕ(x) cos λx dx	<	2	+	2	= ε.

286	Гл. 6. Гармонический анализ
	b
Это означает, что	lim f (x) cos λx dx = 0. Аналогично доказыва-
b	λ→∞ a
b
ется равенство lim	f (x) sin λx dx = 0.
λ→∞

Отметим, что рассматриваемые в теореме 3 пределы дают примеры тех случаев, когда пределы от интегралов не равняются интегралам от пределов подынтегральных функций. Так, например, в случае функции f , равной постоянной, не равной нулю, и конечного промежутка (a, b) подынтегральные выражения в интегралах (51.24) вообще не имеют предела при λ → ∞, а пределы интегралов, как доказано выше, существуют.

51.4. Интеграл Дирихле. Принцип локализации. Займемся теперь изучением сходимости рядов Фурье. Пусть функция f имеет период 2π и абсолютно интегрируема на отрезке [−π, π] (или, как говорят, абсолютно интегрируема на периоде) и

∞

f a0 +	an cos nx + bn sin nx.	(51.32)
	n=1

Сумму Фурье порядка n для функции f будем обозначать Sn(x; f ), или, короче, Sn(x). Найдем для этой суммы выражение, удобное для ее изучения:

Sn(x) = Sn(x; f ) = a0 +

ak cos kx + bk sin kx =

k=1

(51.5)

f (t) dt +

cos kx

f (t) cos kt dt +

sin kx

f (t) sin kt dt =

(51.5) 2π

k=1

−π

π %

+ k=1 cos kx cos kt + sin kx sin kt&f (t) dt =

−

π %

+ k=1 cos k(t − x)&f (t) dt.

(51.33)

Функция

Dn(t) =

+ k=1 cos kt(,

n = 0, 1, 2, ...,

(51.34)

называется ядром Дирихле порядка n.

§ 51. Тригонометрические ряды Фурье

287

Используя обозначение (51.34), из (51.33) получим

π
Sn(x) = Dn(t − x)f (t) dt.	(51.35)

−π

Интеграл, стоящий в правой части этого равенства, называется интегралом Дирихле.

Л е м м а 2. Ядро Дирихле Dn:

1) является четной непрерывной периода 2π функцией;

ππ

2) Dn(t) dt = 2 Dn(t) dt = 1;									(51.36)
−π			0			,	если	t = 2πm,
					t	,	если	t = 2πm,
	sin		n +		1	t


	1		1
3) Dn(t) =		2π sin			2				(51.37)

								±	±
								±	±
	π	n +		2		,	если	t = 2πm,
			n = 0, 1, 2, ...,					m = 0, 1,	2, ...

Свойство 1) очевидным образом следует из формулы (51.34). Фор-

π
мула	Dn(t) dt = 1 получается из (51.34) интегрированием обеих
−π	π
частей этого равенства по отрезку [−π, π], а формула 2 Dn(t) dt = 1
	0

получается из предыдущей в силу четности ядра Дирихле. Докажем

свойство 3). Пусть t = 2πm, m = 0, ±1, ±2, ...;

тогда

(t) =

cos kt

sin

2 sin

cos kt

(51.34)

k=1

(

2π sin

k=1

(

sin n +

sin

k +

sin

2π sin

k=1

−

2π sin

Если же t = 2πm,

m = 0, ±1, ±2, ...,

то

1 1

(2πm) =

+ 1

n +

(51.34) π '2

k=1

(

288 Гл. 6. Гармонический анализ

Нас будет интересовать предел сумм Фурье функции f , т. е. согласно формуле (51.35), предел

nlim Dn(t − x)f (t) dt.	(51.38)
→∞
−π

Отметим, что для нахождения этого предела нельзя, вообще говоря, перейти к пределу при n → ∞ в подынтегральном выражении хотя бы уже потому, что оно, вообще говоря, не имеет этого предела (см. (51.37)).

Для того чтобы найти предел (51.38), докажем для сумм Фурье Sn(x; f ) справедливость одной асимптотической формулы.

Л е м м а 3. Если функция f 2π-периодическая и абсолютно интегрируема на периоде, то

				π
				Sn(x; f ) =	Dn(t)f (x + t) dt,		(51.39)
				−π
				π
				Sn(x; f ) = Dn(t)[f (x + t) + f (x − t)] dt.			(51.40)
				0
	С л е д с т в и е. Для любого δ, 0 < δ π, и любого x [−π, π] имеет
место асимптотическая формула
				δ
	Sn(x; f ) = Dn(t)[f (x + t) + f (x − t)] dt + o(1), n → ∞. (51.41)
				0
1. Докажем формулу (51.39):
				π	π−x
S	;	f )	=		=	Dn(u)f (x + u) du	=
	n(x	f )	(51.35)	Dn(t − x)f (t) dt u=t x		Dn(u)f (x + u) du	. 51.1
					−
				−π	−π−x	π
						= Dn(u)f (x + u) du.
						. 51.1
						−π

2. Для доказательства формулы (51.40) разобьем в формуле (51.39) промежуток интегрирования на отрезки [−π, 0] и [0, π], а затем сделаем в первом интеграле замену переменного t = −u:

Sn(x; f )	=
(51.39)
π	0	π
=	Dn(t)f (x + t) dt = Dn(t)f (x + t) dt + Dn(t)f (x + t) dt =
(51.39)

−π

§ 51. Тригонометрические ряды Фурье			289
π	π
= Dn(−u)f (x − u) du + Dn(t)f (x + t) dt =
0	0	π
		π
	= Dn(t)[f (x + t) + f (x − t)] dt.
		0

(мы воспользовались тем, что Dn(−u) = Dn(u), см. лемму 2, и обозначили u через t).

Докажем теперь следствие, т. е. формулу (51.41).

Зафиксируем произвольно δ, лишь бы выполнялись неравенства 0 < δ π, а затем разобьем промежуток интегрирования в фор-

муле (51.40) на отрезки [0, δ]

и [δ, π]. Тогда, использовав выраже-

ние (51.37) для ядра Дирихле, получим

n(x

;

Dn(t)[f (x + t) + f (x − t)] dt +

f ) (51.37)

(51.40) 0

f (x + t) + f (x − t)

sin

n +

t dt. (51.42)

2π

sin

Функция

непрерывна на отрезке [δ, π],

а функции f (x + t)

sin(t/2)

и f (x − t) как функции переменной t абсолютно интегрируемы на

этом отрезке. Поэтому и функция f (x + t) + f (x − t) абсолютно инте- sin(t/2)

грируема на отрезке [δ, π] (см. замечание в п. 29.5), и, следовательно, согласно теореме Римана (теорема 3 из п. 51.3) имеем

	1	π					1
lim			f (x + t) + f (x − t)		sin	n +		t dt = 0.	(51.43)

n→∞ 2π δ			sin	t		2
				2

Формулы (51.42) и (51.43) означают, что имеет место асимптотическое равенство (51.41).

Отметим, что в формуле (51.41) бесконечно малая o(1) зависит от числа δ и от точки x (см. (51.43)).

Те о р е м а 4 (принцип локализации). Если f является 2π-перио- дической и абсолютно интегрируемой на периоде функцией, то существование предела последовательности ее сумм Фурье Sn(x; f ), n = 1, 2, ..., в любой точке x R равносильно существованию предела

lim Dn(t)[f (x + t) + f (x − t)] dt, (51.44)

→∞

10 Л. Д. Кудрявцев

<<< < Предыдущая 17 18 19 20 21 22 23 24 25 26 27 2829 / 4729 30 31 32 33 34 35 36 37 38 39 40 41 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
24.09.2019317.95 Кб17Копия Т Ф К П.doc
#
10.05.20151.13 Mб11КР по ТПР Чекменёв А.С..docx
#
10.05.2015649.22 Кб91КР_Ромашин_РС110_2012_1.doc
#
24.09.2019131.07 Кб7КРАТКАЯ ХАРАКТЕРИСТИКА ОСНОВНЫХ АХОВ.doc
#
10.05.20155.57 Mб813Краткий курс математического анализа. Том 1.pdf
#
10.05.20154.49 Mб383Краткий курс математического анализа. Том 2.pdf
#
22.12.2019144.9 Кб0Кратко 31-40.doc
#
10.05.20151.56 Mб92краткое сожержание курса БЖД.doc
#
16.11.201929.92 Кб34кризис.docx
#
16.03.20162.51 Mб740Криминология Малков В. Д..doc
#
27.11.2019524.29 Кб78Курс лекций Интернет-технологии.doc