5.5. Однородные системы линейных уравнений.

Если в системе

все свободные члены равны нулю, то система называется однородной. Однородная система имеет вид

(9)

I) Из теоремы Кронекера –Капелли вытекает, что эта системасовместна всегда, так как добавление столбца из нулей не может повысить ранг расширенной матрицы. Система (9) всегда имеет нулевое решение.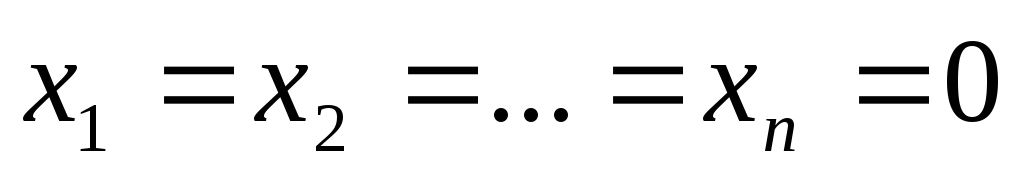

II) Пусть:

• Если , то есть число уравнений совпадает с числом неизвестных, то с помощью алгоритма Гаусса система приводится к виду

,

где ,,.

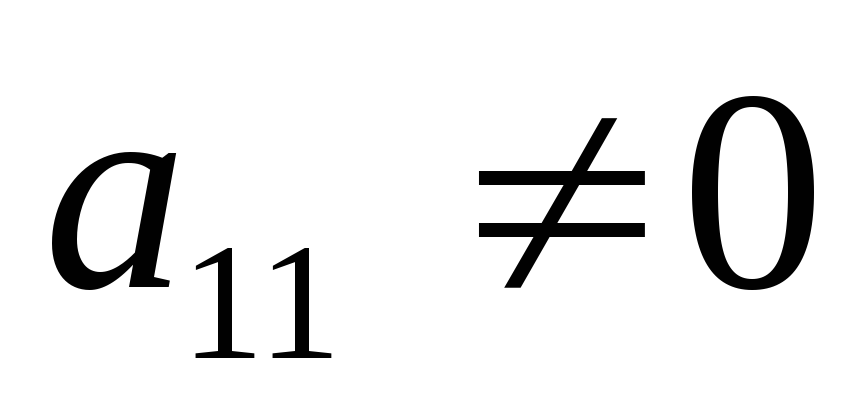Эта система имеет единственное нулевое решение .

• Если , то уравнений меньше чем неизвестных и систему алгоритмом Гаусса можно привести к виду

где ,,. Эта система имеет бесконечное множество ненулевых решений.

Теорема.

1. Однородная система линейных уравнений всегда совместна.

2. Если ранг матрицы Аоднородной системы равен числу неизвестных (), то система имеет единственное решение.

3. Если ранг матрицы Аоднородной системы меньше числа неизвестных (),то система всегда имеет ненулевое решение.

Пример.Решить систему

Решение. Выпишем расширенную матрицу системы и приведём её к ступенчатому виду.

(10)

Последняя матрица соответствует системе, эквивалентной исходной. Выберем базисный минор в первом и третьем столбце, имеющий вид . При таком выборе базисными неизвестными являютсяи, а свободнымии.

Запишем эквивалентную систему по последней матрице в цепочке (10) и решим её:

Ответ: .