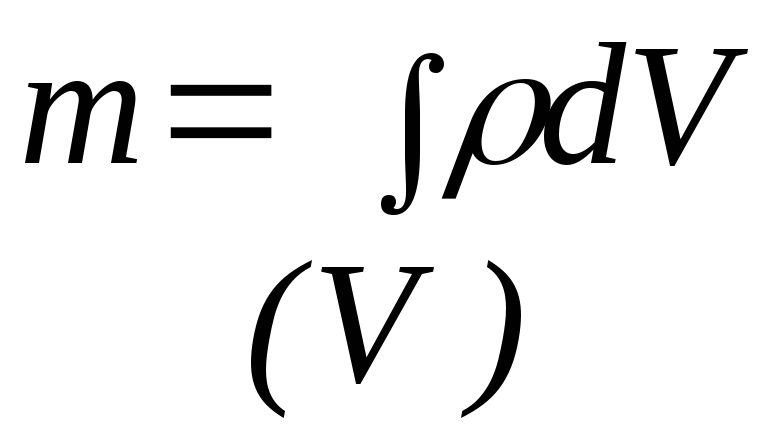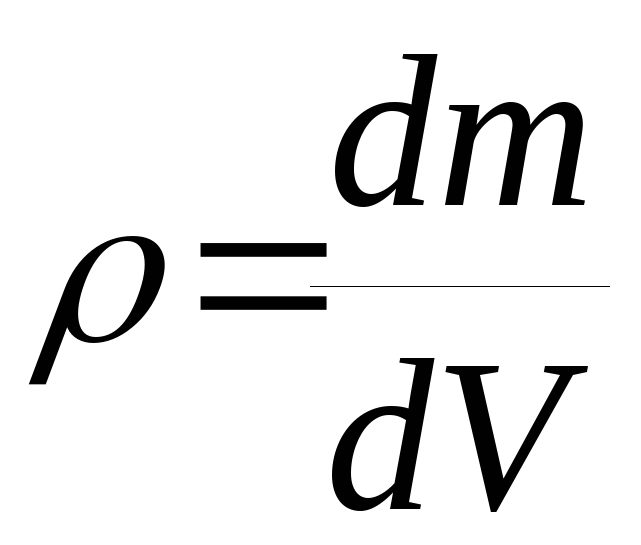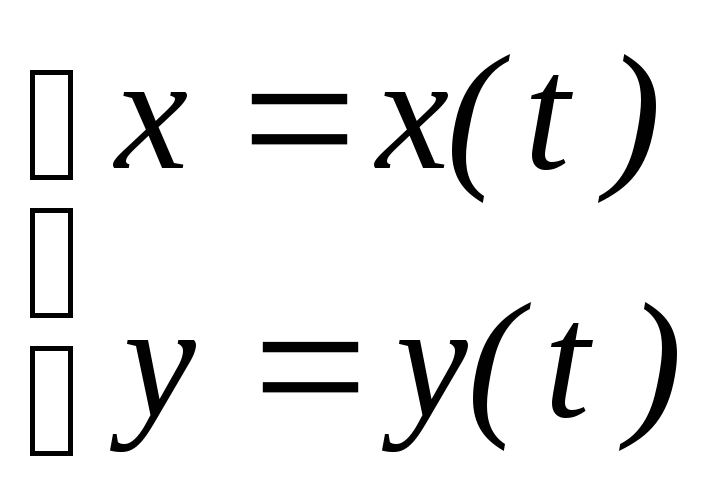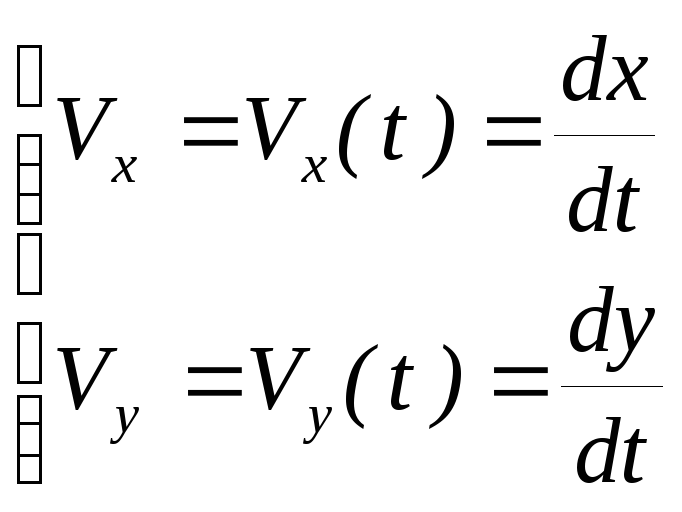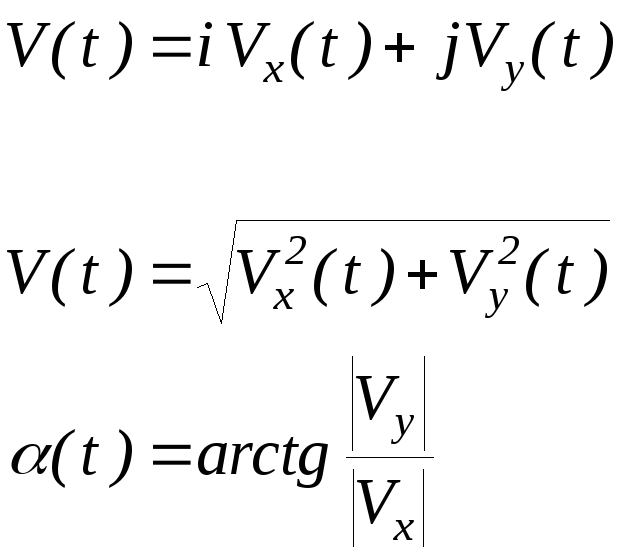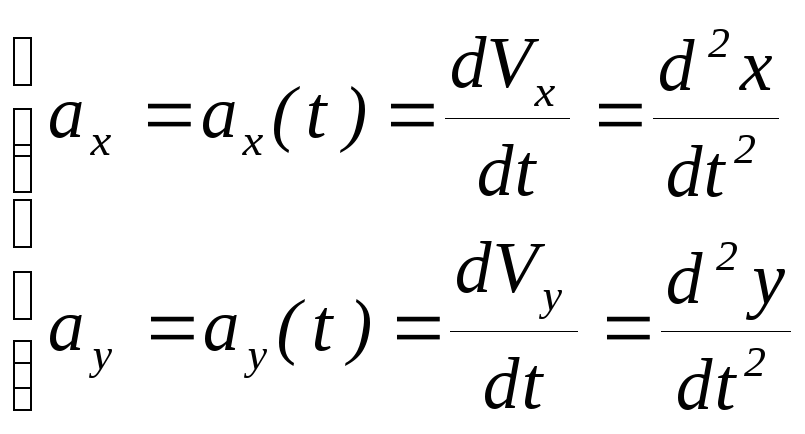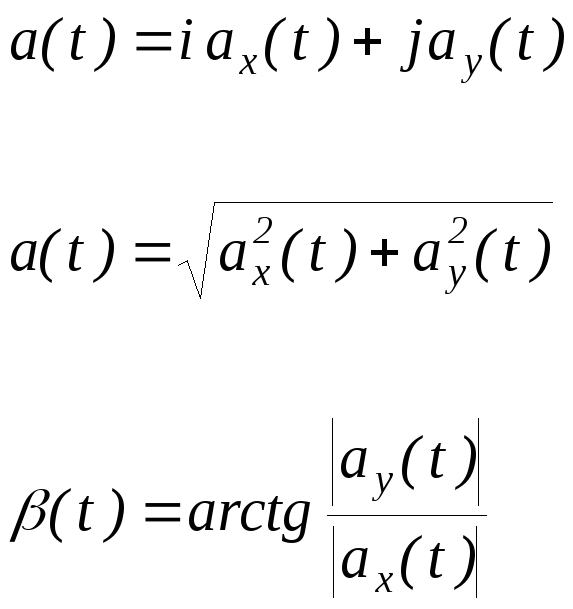Механика теор
.docКинематика и динамика материальной точки. Теоретический минимум.
|
|
№ |
Вопрос |
Формула |
Размерность |
Пояснения, определения |
||||
|---|---|---|---|---|---|---|---|---|---|
|
|
1 |
Тело отсчёта |
|
|
Тело, по отношению к которому рассматривается данное механическое движение, называется телом отсчета. |
||||
|
|
2 |
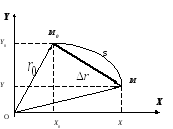
Радиус-вектор |
|
|
Вектор,
проведенный из начала координат в
интересующую нас точку, называют
радиусом – вектором
|
||||
|
|
3 |
Материальная точка
|
Материальной точкой называется тело, размерами которого в условиях данной задачи можно пренебречь. |
||||||
|
|
4 |
Система отсчёта |
|
Совокупность тела отсчета, связанной с ним системы координат, снабженной часами, называется системой отсчета.
|
|||||
|
|
5 |
Траектория |
|
Непрерывную линию, которую описывает в пространстве движущаяся материальная точка, называют траекторией. По форме, траектории механического движения делятся на прямолинейные и криволинейные. Траектории данного механического движения в разных системах отсчета могут иметь неодинаковую форму.
|
|||||
|
|
6 |
Перемещение |
|
|
Перемещение тела – вектор, соединяющий начальное и конечное положения материальной точки. |
||||
|
|
7 |
Путь |
|
[S]
=
|
Путь S – скалярная величина, равная длине участка траектории, пройденного движущейся точкой за данный промежуток времени. |
||||
|
|
8 |
Скорость
|
|
[V]= [1 м/с] |
Мгновенной скоростью (скоростью)
называется векторная физическая
величина, характеризующая быстроту
изменения положения точки в пространстве,
равная производной первого порядка
от радиус-вектора
Вектор скорости направлен по касательной к траектории.
где «+» соответствует случаю
|
||||
|
|
9 |
Ускорение |
|
|
Ускорением (мгновенным ускорением)
тела в момент времени
Направление вектора ускорения
совпадает с направлением изменения
вектора скорости
|
||||
|
|
10 |
Тангенциальая составляющая ускорения |
|
|
|||||
|
|
11 |
Нормальная составляющая ускорения |
|
Если
|
|||||
|
|
12 |
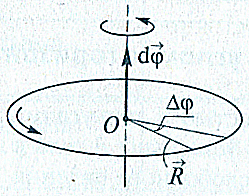
Элементарное угловое перемещение |
|
|
Поворот тела в пространстве за
бесконечно малый интервал времени dt
характеризуется псевдовектором
углового перемещения
|
||||
|
|
13 |
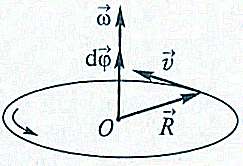
Угловая скорость |
|
|
Угловой
скоростью
|
||||
|
|
14 |
Угловое ускорение |
|
|
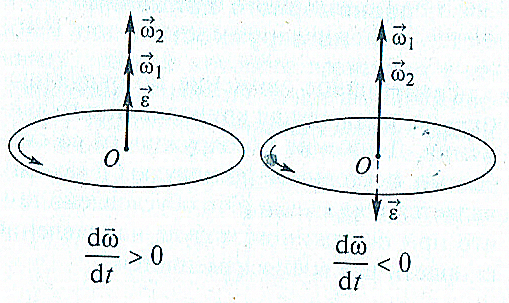
Угловое ускорение - псевдовектор, характеризующий быстроту изменения угловой скорости, равный первой производной от вектора угловой скорости по времени и второй производной от угловой координаты.
Псевдовектор углового ускорения,
как и всякий псевдовектор, характеризующий
вращательное движение, направлен
вдоль оси вращения перпендикулярно
плоскости вращения. Псевдовектор
углового ускорения сонаправлен с
псевдовектором угловой скорости (
|
||||
|
|
15 |
Связь линейных и угловых характеристик движения |
|
П
|
|||||
|
|
Описание движения в линейных и угловых характеристиках |
||||||||
|
|
Линейные величины |
Угловые величины |
|||||||
|
|
|
|
|||||||
|
|
|
|
|||||||
|
|
|
||||||||
|
|
|
|
|||||||
|
|
|
||||||||
|
|
Произвольное движение |
||||||||
|
|
|
«+» - при увеличении скорости вращения, «-» - при уменьшении скорости вращения.
|
|||||||
|
|
Равноускоренное движение |
||||||||
|
|
|
«+» - при увеличении скорости вращения, «-» - при уменьшении скорости вращения.
|
|||||||
|
|
Равномерное движение |
||||||||
|
|
|
|
|||||||
|
|
16 |
Период вращения Т |
Т = 1с
|
Периодом вращения Т называют
время одного полного оборота ( |
|||||
|
|
17 |
Частота вращения |
|
Частотой вращения n называют количество оборотов, совершаемых телом за единицу времени |
|||||
|
|
18 |
Преобразования Галилея:
Закон сложения перемещений:
Закон сложения скоростей:
Закон сложения ускорений: |
t=t′
|
|
|||||
|
|
19 |
Первый закон Ньютона: |
Существуют инерциальные системы отсчёта, относительно которых поступательно движущееся тело сохраняет состояние равномерного прямолинейного движения, если действие внешних сил на него взаимно скомпенсировано. |
||||||
|
|
20 |
Инерциальная система отсчёта: |
система отсчёта, относительно которой материальная точка, на которую не действуют внешние силы или их действие взаимно скомпенсировано, покоится или движется равномерно прямолинейно. |
||||||
|
|
21 |
Масса тела: |
|
[m]
=
|
Массой тела называется положительная скалярная величина, являющаяся мерой инертности тела в поступательном движении.
|
||||
|
|
22 |
Плотность тела |
|
|
Плотностью
|
||||
|
|
23 |
Импульс материальной точки |
|
[p]= [1 кг*м/с] |
Импульсом
|
||||
|
|
24 |
Сила |
Силой
|
||||||
|
|
25 |
Равнодействующая сил |
|
[F]= [1Н]= =[1 кг*м/с2] |
Сила, равная геометрической сумме всех приложенных к материальной точке сил и оказывающая эквивалентное им действие, называется равнодействующей силой. |
||||
|
|
26 |
Второй закон Ньютона (общий вид): В случае постоянной массы m=const |
|
Действие на тело внешних сил,
равнодействующая которых равна
Ускорение, приобретаемое телом
(материальной точкой) совпадает по
направлению с равнодействующей
|
|||||
|
|
27 |
Третий закон Ньютона: |
|
Тела взаимодействуют друг с другом силами одной природы, равными по модулю и противоположными по направлению. |
|||||
|
Закон движения:
|
|
|
|
|
|||||
|
Система уравнений движения:
|
|
Уравнение траектории: |
|
|
|||||
|
Законы изменения проекций скорости:
|
|
Законы изменения вектора скорости, модуля скорости, направления скорости: |
|
|
|||||
|
Законы изменения проекций ускорения: |
|
Законы изменения вектора ускорения, модуля ускорения,
направления ускорения - зависимость от времени радиуса кривизны траектории |
|
|
|||||

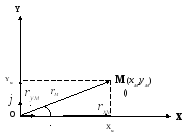
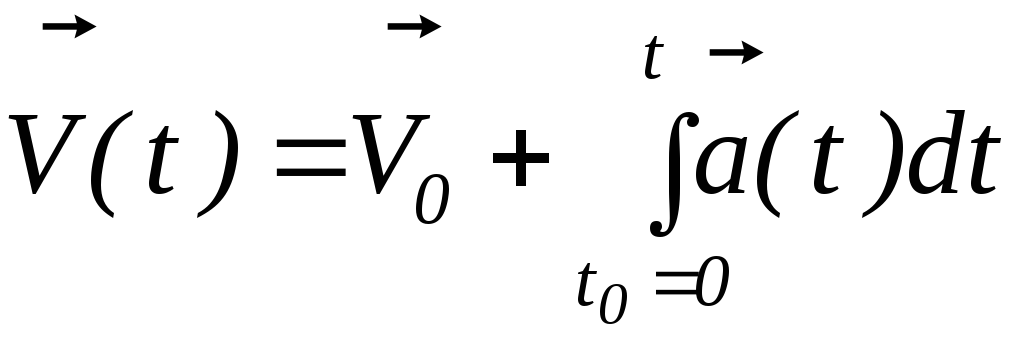

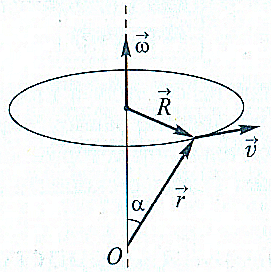 оложение
рассматриваемой точки задаётся
радиус-вектором
оложение
рассматриваемой точки задаётся
радиус-вектором