Фдз 1. Матрицы. Операции над матрицами.
Операции с матрицами: равенство матриц; умножение матрицы на число; сложение матриц; перемножение матриц.
Транспонирование матрицы.
Квадратные, треугольные, диагональные, симметричные матрицы. Единичная матрица.
Возведение квадратной матрицы в натуральную степень.
1. Для матриц
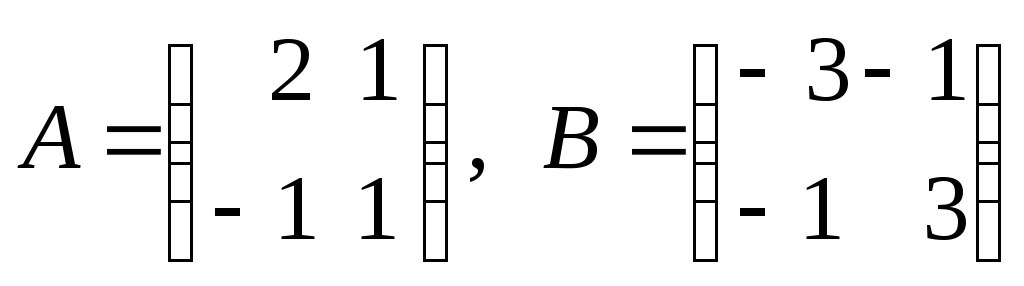найти:
.
2. Для матриц найти:
.
3.
.
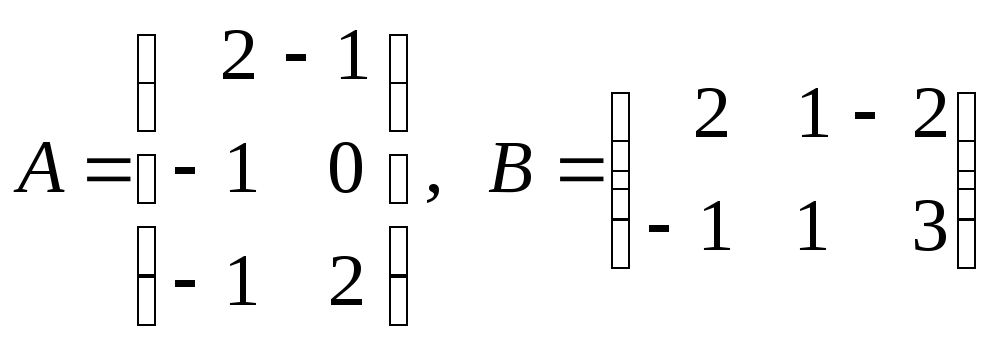Выполнить те из операций, которые
указаны ниже
(в случае невыполнимости операции указать причину невыполнимости):
.
4.
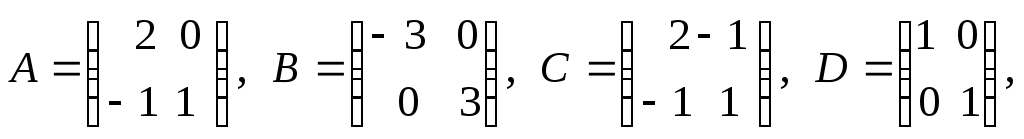
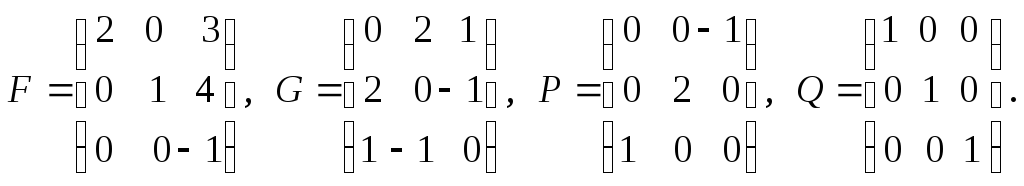
Какие из приведенных выше матриц являются:
1) симметрическими; 2) диагональными; 3) треугольными; 4) единичными.
________________________________________________________________________
Домашнее задание.
1. Для заданных матриц
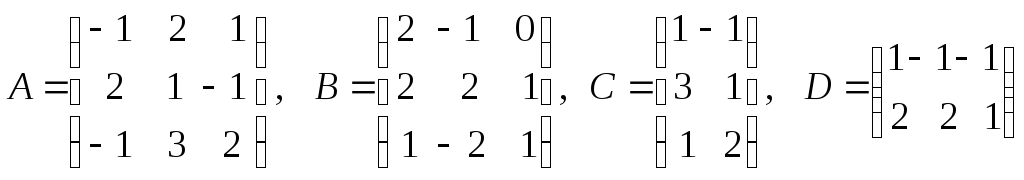
найти
.
Фдз 2. Определители.
Определитель
-го
порядка. Правила Саррюса вычисления
определителей 2-го и 3-го порядков.
Основные свойства определителей.
1. Установить четность (нечетность)
перестановок:
.
2. Дать определение определителя
го
порядка.
3. Записать правила Саррюса вычисления определителей 1-го, 2-го, 3-го порядков.
4. Вычислить по правилам Саррюса определители:
.
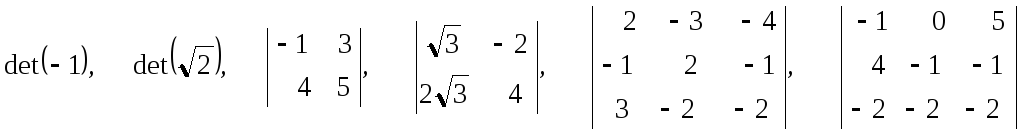5. Сформулировать основные свойства определителей.
6. Почему можно не вычисляя указанных ниже определителей сразу сказать, что каждый из них равен нулю?
.
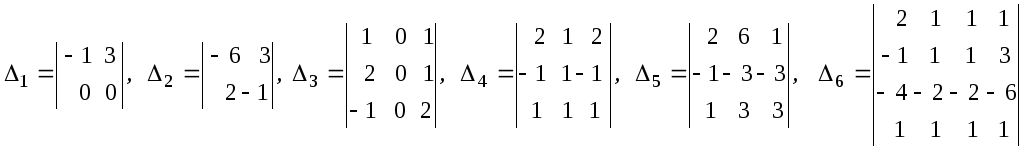7. Вычислить определители:
.
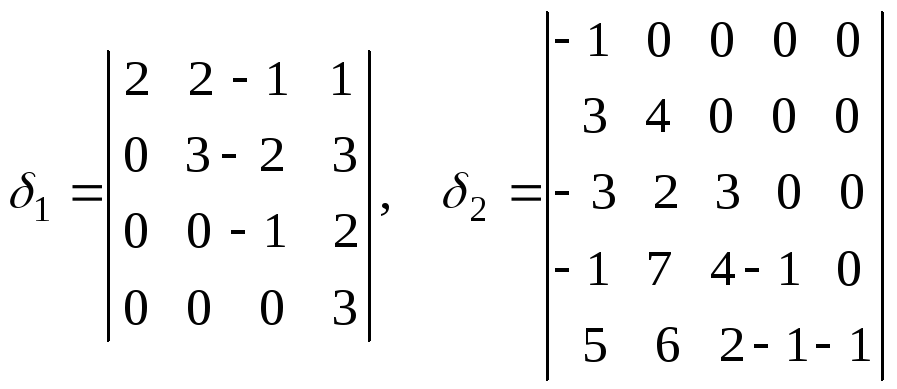8. Вычислить следующие определителя, сведя их к определителям треугольных матриц:
.
___________________________________________________________________________
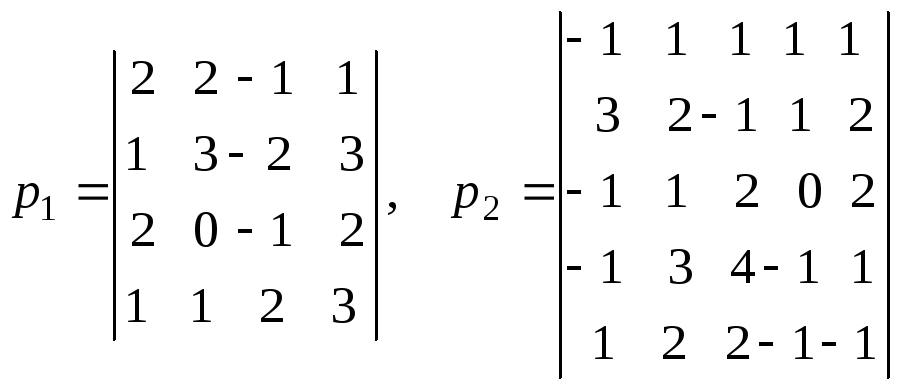Домашнее задание.
1. Определить четность перестановки
.
2. Даны квадратные матрицы
,
,
,
.
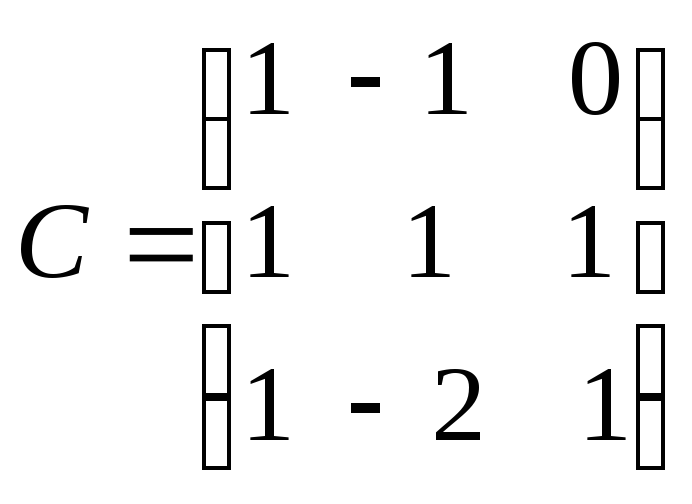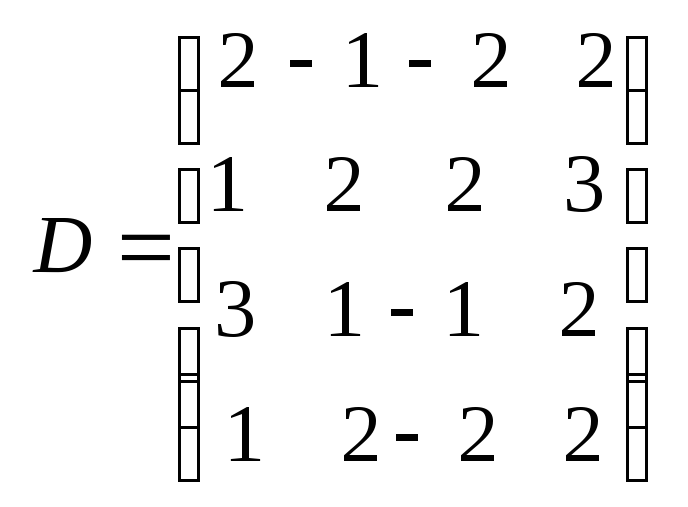1) Вычислить определители матриц
по правилам Саррюса.
2) Вычислить определитель матрицы
с помощью свойств
определителей (сведя его к определителю
матрицы треугольного вида).
Фдз 3. Определители (продолжение). Обратная матрица
Миноры и алгебраические дополнения.
Разложение определителя по строке (столбцу).
Обратная матрица, ее нахождение.
1. Сформулировать теорему о разложении определителя по строке (столбцу).
2. Найти миноры
и алгебраические дополнения
для матрицы
.
Вычислить затем
тремя способами:
по правилу Саррюса; разложением по 2-й строке; разложением по 1-му столбцу.
3. Найти миноры и алгебраические дополнения для матрицы . Вычислить затем тремя способами:
по правилу Саррюса; разложением по 3-й строке; разложением по 2-му столбцу.
4. Вычислить определитель
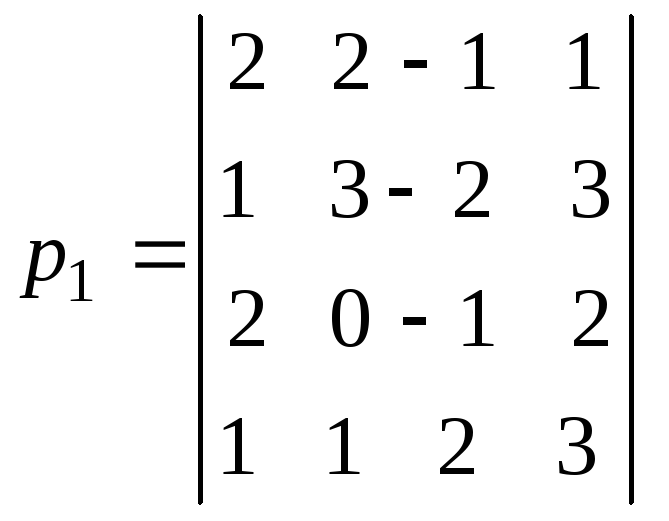двумя способами:
разложением по 2-й строке; разложением по 3-му столбцу.
5. Дать определение обратной матрицы.
6. Найти обратные матрицы для матриц (если это невозможно, указать причину):
.
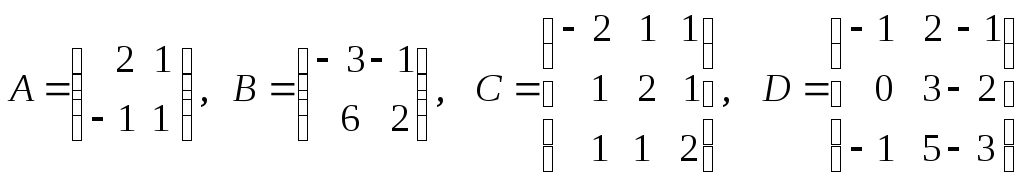Выполнить проверку найденных обратных матриц.
_________________________________________________________________________
Домашнее задание.
1. Дана матрица
.
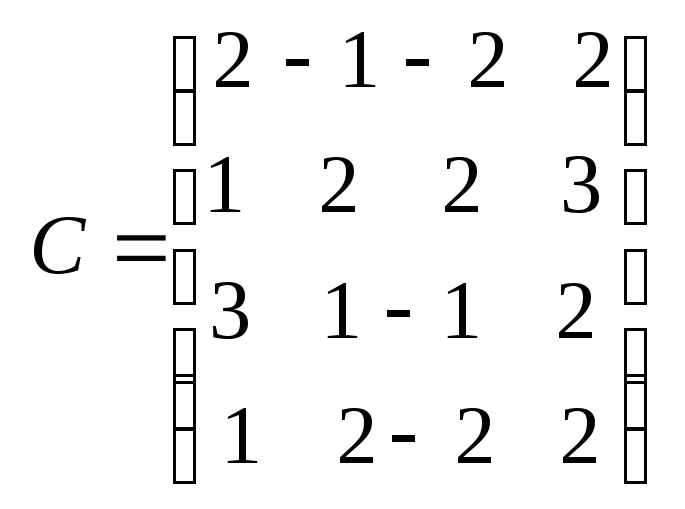Найти миноры
и алгебраические дополнения
Вычислить определитель матрицы
двумя способами:
а) разложением по 3-й строке; б) разложением по 4-му столбцу.
2. Найти обратные матрицы для матриц
,
.
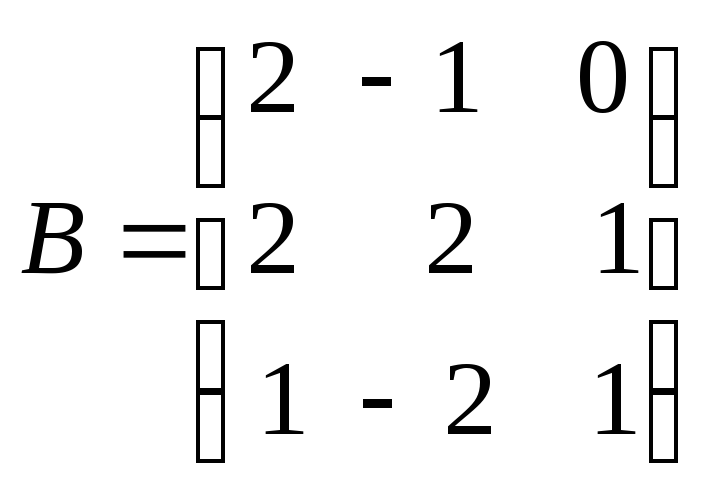