LK / Лекция 35

Баранов Виктор Павлович. Дискретная математика. Раздел 7. Элементы теории алгоритмов. Лекция 35. Формальное определение алгоритма. Представление об алгоритмически неразрешимых проблемах

Лекция 35. ФОРМАЛЬНОЕ ОПРЕДЕЛЕНИЕ АЛГОРИТМА.

АЛГОРИТМИЧЕСКИ НЕРАЗРЕШИМЫЕ ПРОБЛЕМЫ

План лекции:

1. Формальное определение алгоритма.

2. Представление об алгоритмически неразрешимых проблемах.

1. Формальное определение алгоритма

Определение. Словарный оператор

называется вычислимым по Тьюрингу, если существует машина Тьюринга с алфавитом ленты , которая работает следующим образом: если на ленту записать произвольное слово , установить головку на правый символ и запустить машину по ее программе, то после остановки машины на ленте будет написано слово .

Приведем одно из возможных формальных определений алгоритма:

алгоритм – это словарный оператор, вычислимый по Тьюрингу.

2. Представление об алгоритмически неразрешимых проблемах

Определение алгоритма состоит в том, что если ранее это понятие существовало на неточном, интуитивном уровне, то теперь ему сопоставлен некоторый точно определенный объект – программа машины Тьюринга. Фактически программа представляет собой слово в некотором алфавите и можно себе представить, что, анализируя какую-либо проблему, мы придем к выводу о несуществовании указанного слова, тем самым к алгоритмической неразрешимости проблемы.

Приведем несколько примеров алгоритмически неразрешимых проблем.

Первый результат об алгоритмической неразрешимости был получен в 1947 г. независимо друг от друга А.А. Марковым и Э.Л. Постом по проблеме равенства в полугруппах.

1. Проблема равенства в полугруппах.

Полугруппой или ассоциативной системой называют множество, на котором определена одна ассоциативная операция. Примером полугруппы является совокупность всевозможных слов в алфавите

(1)

с операцией конкатенации. называется свободной полугруппой с образующими. Свободная полугруппа с одной образующей состоит из слов и изоморфна полугруппе неотрицательных целых чисел с операцией сложения.

На основе свободной полугруппы можно построить новые полугруппы при помощи определяющих соотношений. Пусть

(2)

есть произвольная совокупность пар слов из . Элементарным преобразованием называется переход от слова к слову или обратно. Два слова из называются эквивалентными, если от одного можно перейти к другому конечным числом элементарных преобразований.

Проблема равенства слов в полугруппе заключается в отыскании алгоритма, устанавливающего эквивалентность любой пары слов.

Пусть определяющие соотношения имеют вид

.

Составом слова назовем вектор , где – количество букв в слове , . Элементарные преобразования не изменяют состав слова, причем каждое слово можно привести к виду

,

в котором буквы стоят в алфавитном порядке. Отсюда следует, что два слова эквивалентны в том и только том случае, когда они имеют одинаковый состав, что и дает алгоритм эквивалентности для данной полугруппы.

А.А. Марков и Э.Л. Пост построили примеры полугрупп, для которых алгоритма распознавания равенства (эквивалентности) не существует. В дальнейшем число таких примеров значительно увеличилось. Приведем пример Г.С. Цейтлина: полугруппа с образующими и определяющими соотношениями

имеет неразрешимую проблему равенства слов.

2. Проблема полноты автоматного базиса.

Ранее была сформулирована задача о полноте автоматного базиса: для заданного набора структурных автоматов требуется установить возможность построения на их основе любого наперед заданного автомата.

В 1964 г. М.И. Кратко установил алгоритмическую неразрешимость задачи о полноте автоматного базиса. Это означает, что не существует машины Тьюринга, работающей следующим образом: если на ленту машины поместить описания автоматов и запустить ее в работу, то машина остановится в состоянии !, если система полная и в состоянии !!, если эта система неполная.

3. 10-я проблема Гильберта.

В 1900 г. на II Международном Конгрессе математиков Д. Гильберт выступил с докладом «Математические проблемы», в котором сформулировал 23 проблемы , «исследование которых может значительно стимулировать развитие науки». Десятая из этих проблем называется «Задача о разрешимости диофантова уравнения».

Пусть задано диафантово уравнение с произвольными неизвестными и целыми рациональными чис ловыми коэффициентами. Указать способ, при помощи которого возможно после конечного числа операций установить разрешимо ли это уравнение в целых рациональных числах.

Диофантовым называют уравнение вида

, (3)

в котором – многочлен -ой степени от переменных с целыми коэффициентами:

.

В 1970 г. Ю.И. Митиясевич доказал, алгоритма, устанавливающего разрешимость диофантова уравнения не существует.

4. Проблема остановки машины Тьюринга.

Так как набор инструкций для машины Тьюринга может быть задан произвольно, то возможны ситуации, когда машина работает без остановки, то есть не переходит в заключительное состояние. Рассмотрим, например, машину с программой

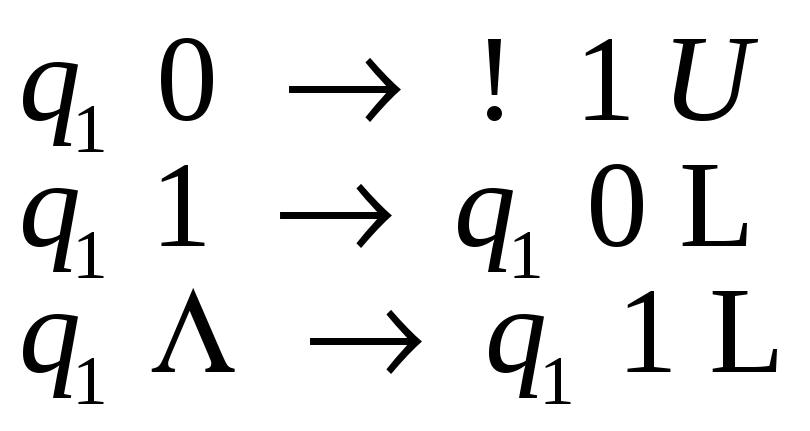
Машина с данной программой будет работать следующим образом: если в начальном слове на ленте есть нули, то дойдя до первого из них машина остановится; если начальное слово состоит из одних единиц, то головка будет без остановки перемещаться влево.

Проблема остановки машины Тьюринга состоит в следующем: для данной машины Тьюринга и данного слова требуется установить остановится ли машина, начав работу с правого символа слова или нет.

Можно доказать, что не существует алгоритма для решения этой проблемы.

3