LK / Лекция 34

Баранов Виктор Павлович. Дискретная математика. Раздел 7. Элементы теории алгоритмов.

Лекция 32. Вычислимые функции и операции суперпозиции, примитивной рекурсии и минимизации

Лекция 32. ВЫЧИСЛИМЫЕ ФУНКЦИИ И ОПЕРАЦИИ СУПЕРПОЗИЦИИ, ПРИМИТИВНОЙ РЕКУРСИИ И МИНИМИЗАЦИИ

План лекции:

1. Определение операций суперпозиции, примитивной рекурсии и минимизации.

2. Применение операций суперпозиции, примитивной рекурсии и минимизации к вычислимым функциями.

1. Определение операций суперпозиции, примитивной рекурсии и минимизации

На множестве определим три операции: (суперпозиция), (примитивная рекурсия) и (минимизация).

Операция суперпозиции вводится так же, как и для булевой алгебры

Операция примитивной рекурсии определяется следующим образом.

Пусть и – произвольные функции из . Построим функцию , используя «схему» примитивной рекурсии:

, .

Пусть – произвольный набор чисел из . Полагаем

.

Если на этом наборе определена, то полагаем

.

Через конечное число шагов мы либо определим , либо установим, что на этом наборе не определена. Говорят, что функция получена из функций и при помощи операции примитивной рекурсии.

Операция минимизации определяется следующим образом. Пусть – произвольная функция из . Построим функцию через оператор минимизации

,

что означает, что для произвольного набора составляется уравнение

.

а) Если существует из , являющееся решением этого уравнения, то берем минимальное из решений, обозначаем его через и полагаем

.

б) В противном случае функция не определена.

Про функцию говорят, что она получена из функции при помощи операции минимизации.

Данные операции позволяют построить три следующие функциональные системы.

1. Множество 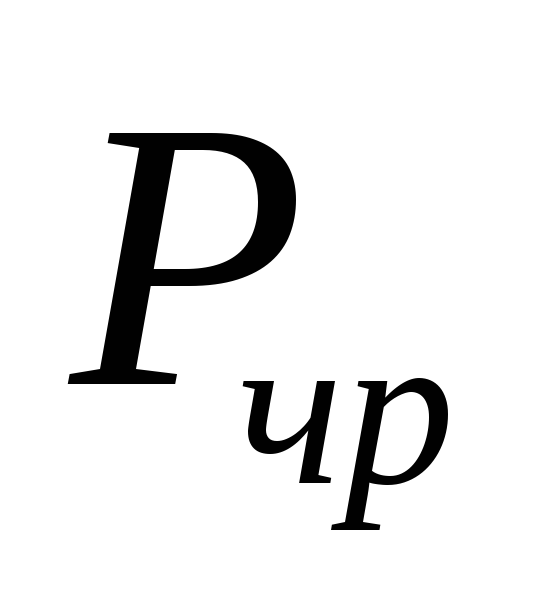всех функций, которые можно получить из системы 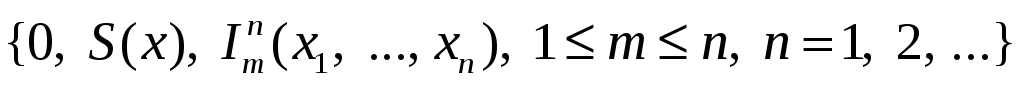при помощи операци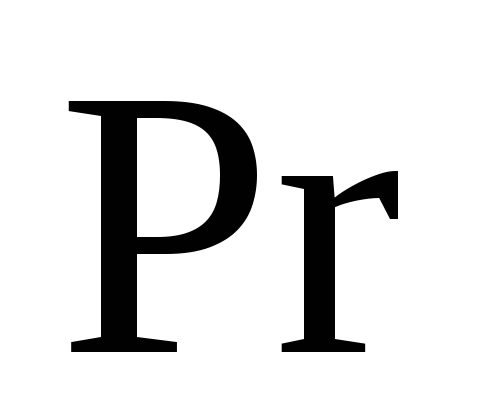й , и , называемое классом частично-рекурсивных функций.

2. Класс рекурсивных функций, т. е. множество всех всюду определенных функций из .

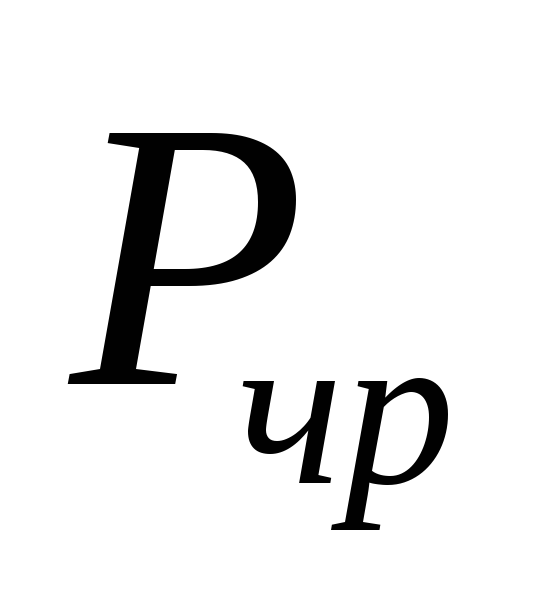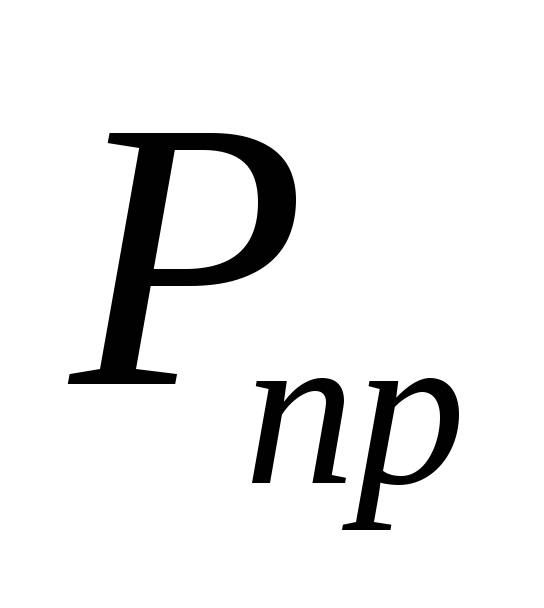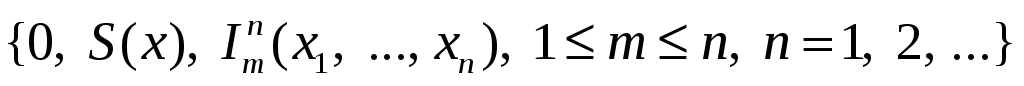3. Класс примитивно-рекурсивных функций, т. е. множество всех функций, которые можно получить из системы при помощи операций и .

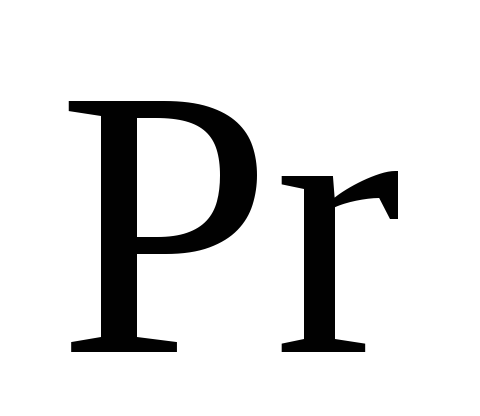Очевидно, что

.

2. Применение операций суперпозиции, примитивной рекурсии и минимизации к вычислимым функциями

Лемма 1. Из вычислимой функции при добавлении и изъятии несущественных переменных получается вычислимая функция.

Лемма 2. Если

, , …,

вычислимы, то функция

также вычислима.

Теорема 1. Класс замкнут относительно операции суперпозиции.

Теорема 2. Класс замкнут относительно операции .

Теорема 3. Класс замкнут относительно операции .

Теорема 4. Класс замкнут относительно операций .

Следствие. .

2