5. Задача о полноте автоматного базиса

Набор структурных автоматов называется полным (или автоматным базисом), если из них можно построить любой наперед заданный структурный автомат.

Усилия математиков для получения аналога теоремы Поста для автоматов не увенчались успехом. В 1964 г. М.И. Кратко доказал несуществование алгоритма для определения полноты системы . В этом случае представляют интерес варианты теоремы о полноте с дополнительными предположениями о системе . Рассмотрим наиболее популярный из них.

Теорема. Система автоматов , содержащая полный набор ФЭ и -триггер (или -триггер) является полной.

Доказательство. Рассмотрим произвольный автомат , заданный соотношениями (2), и опишем его схему из указанных автоматов, называемую канонической структурой (рис. 6).

Схема состоит из двух частей.

…

СФЭ

…

…

Рис. 6.

Левая половина называется запоминающей частью. Она состоит из триггеров, набор состояний которых образует состояние автомата: если в момент времени

, …, ,

то это означает, что автомат находится в состоянии .

Правая половина называется комбинационной частью и представляет СФЭ. Входы этой схемы:

1. двоичное слово – входной сигнал автомата ;

2. двоичное слово – текущее внутреннее состояние автомата .

Выходы:

1. двоичное слово – выходной сигнал автомата , который реализуется по формулам (3);

2. двоичное слово 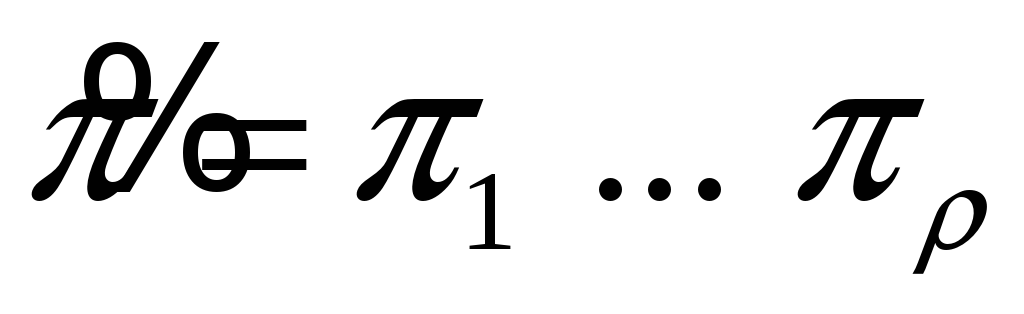, которое поступает на входы триггеров в запоминающей части и управляет памятью автомата.

Покажем, что сигналы управления памятью являются булевыми функциями от тех же переменных, что и выход автомата, а, значит, они могут быть реализованы полной системой ФЭ.

В каждый момент времени сигналы управления памятью должны переводить автомат из состояния в состояние . Для этого надо изменить состояние каждого триггера

, .

Используемые в канонической схеме -триггеры или -триггеры обладают следующим свойством: для любой пары состояний существует входной сигнал, переводящий автомат из состояния в состояние . Обозначим этот сигнал через . Для -триггера , так как состояние, в которое устанавливается -триггер, равно входному сигналу. Для -триггера : при на вход надо подать 0, чтобы состояние не изменилось; при – 1, чтобы триггер «перевернулся».

Итак, , или в векторной форме

.

Выразим из закона функционирования автомата (2). Тогда

.

Теорема доказана.

6. Канонический метод синтеза автомата

Рассмотрим этот метод на конкретном примере.

Пример. На конвейере, по которому двигаются детали двух типов и , установлен автомат, задачей которого является такая сортировка деталей, чтобы после прохождения мимо автомата они образовывали группы . Неподходящую деталь автомат сталкивает с конвейера. Требуется построить схему такого автомата, используя -триггер и элементы «И», «ИЛИ», «НЕ».

Синтез автомата разбивается на следующие этапы.

1. Построение абстрактного автомата .

Входной алфавит – . Выходной алфавит – , где С – сталкивание детали, П – ее пропуск. Внутренние состояния автомата отражают его память о том, какую часть группы он уже сформировал: . По мере формирования группы автомат циклически перемещается по этим состояниям, не изменяя состояния при поступлении неподходящей детали. Диаграмма переходов-выходов показана на рис. 7.

| | |

| |

|

Рис. 7.

2. Кодирование алфавитов .

Один из возможных вариантов кодирования приведен в следующих таблицах.

Вход Выход Состояние

A	0		С	0			00
B	1		П	1			01
							11

3. Построение канонической структуры автомата.

Каноническая структура разрабатываемого автомата показана на рис. 8.

СФЭ

Рис. 8.

Найдем зависимости выходов СФЭ , от переменных сначала в табличном виде (таблица 8), по которым далее построим формулы

, , .

Таблица 8

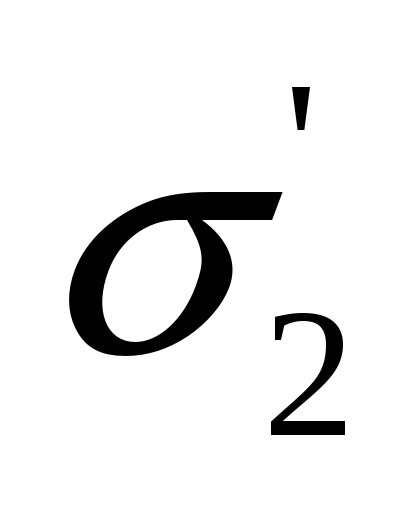
0	0	0	1	0	1	0	1
0	0	1	0	0	1	0	0
0	1	0	*	*	*	*	*
0	1	1	0	1	1	0	0
1	0	0	0	0	0	0	0
1	0	1	1	1	1	1	0
1	1	0	*	*	*	*	*
1	1	1	1	0	0	1	1

Эти функции называются частично определенными, так как они не определены при . Для представления этих функций формулами их доопределяют таким образом, чтобы получить более простой вид формул.

4. Представление функций выхода автомата и функций управления памятью формулами.

Используя методы минимизации булевых функций, строим по возможности экономное представление функций , , формулами в базисе :

,

,

.

5. Реализация СФЭ и окончательная схема автомата (рис. 9).

НЕ

И

И

И

ИЛИ

ИЛИ

Рис. 9.

9