Баранов Виктор Павлович. Дискретная математика. Раздел 6. Конечные автоматы и формальные языки.

Лекция 31. Определение и способы задания конечного автомата. Задача синтеза. Элементарные автоматы

Лекция 31. ОПРЕДЕЛЕНИЕ И СПОСОБЫ ЗАДАНИЯ КОНЕЧНОГО АВТОМАТА.

Задача синтеза. Элементарные автоматы

План лекции:

1. Определение конечного автомата.

2. Способы задания конечного автомата.

3. Задача синтеза автоматов.

4. Элементарные автоматы.

5. Задача о полноте автоматного базиса.

6. Канонический метод синтеза автомата.

1. Определение конечного автомата

СФЭ не учитывают тот факт, что реальные устройства работают во времени. По сравнению с СФЭ конечный автомат является более точной моделью дискретного преобразователя информации. При этом понятие конечного автомата, как и любая модель, связано с рядом упрощающих предположений.

Во-первых, предполагается, что вход и выход автомата в каждый момент времени может находиться только в одном из конечного числа различных состояний. Если реальный преобразователь имеет непрерывный входной сигнал, то для его описания с помощью конечного автомата необходимо провести квантование этого сигнала. В формальном определении автомата конечный набор состояний входа и выхода автомата называется соответственно входным и выходным алфавитом, а отдельные состояния – буквами этих алфавитов.

Во-вторых, предполагается, что время изменяется дискретно. Состояния входа и выхода соответствуют дискретной временной последовательности Поскольку момент времени однозначно определяется его индексом, то с целью упрощения будем считать, что время принимает значения 1, 2, …, , … Временной промежуток называется тактом.

Работа автомата представляется следующим образом.

На вход автомата поступают сигналы из входного алфавита , что приводит к появлению сигналов на выходе из входного алфавита . Зависимость выходной последовательности от входной зависит от внутреннего устройства автомата. Заметим, что в отличие от СФЭ, которые не обладают памятью, автомат представляет собой устройство с памятью, т. е. выход автомата определяется не только входом , но и предысторией . Учет предыстории осуществляется зависимостью выходного сигнала не только от входа, но и от текущего состояния, которое обозначим .

Дадим формальное определение автомата.

Конечным автоматом называют пятерку объектов

, (1)

где

– конечное множество, называемое входным алфавитом; – одно из возможных состояний входа;

– конечное множество, называемое выходным алфавитом; элементы этого множества определяют возможные состояния выхода;

– конечное множество, называемое алфавитом внутренних состояний;

– функция переходов автомата: ; эта функция каждой паре «вход-состояние» ставит в соответствие состояние;

– функция выходов автомата: ; эта функция каждой паре «вход-состояние» ставит в соответствие значение выхода.

Закон функционирования автомата: автомат изменяет свои состояния в соответствии с функцией и вырабатывает выходные сигналы в соответствии с функцией :

, ,

2. Способы задания конечного автомата

1. Табличный способ задания. Поскольку для функций и области определения и значений принадлежат конечному множеству, то их задают при помощи таблиц.

Пример 1. Зададим автомат следующим образом: , , .Функцию определим с помощью таблицы переходов, а функцию – с помощью таблицы выходов.

Таблица 1. Таблица переходов Таблица 2. Таблица выходов

	Вход	Состояние

Вход	Состояние

Если известна последовательность сигналов на входе автомата, то таблицами переходов и выходов однозначно определяется выходная последовательность.

2. Графический способ задания. Используется диаграмма переходов-выходов. Она представляет собой ориентированный мультиграф, в котором каждому внутреннему состоянию автомата соответствует вершина. Переходы автомата из состояния в состояние изображаются стрелками, на каждой из которых пишутся входной символ, вызывающий данный переход, и выходной символ, вырабатываемый автоматом.

| | |

| |

| |

|

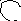
Рис.1 Диаграмма переходов-выходов

Пример 2. Требуется построить автомат, который работал бы следующим образом: в каждый такт на вход автомата поступают очередные двоичные разряды слагаемых, автомат вырабатывает соответствующий двоичный разряд их суммы. Для двухразрядных слагаемых имеем: , , .

Автомат находится в состоянии 1, если при сложении предыдущих разрядов возникает перенос, и в состоянии 0 – в противном случае. Диаграмма переходов-выходов показана на рис. 2.

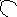
00|0 11|1 01|0

01|1 10|0

10|1 00|1 11|1

Рис. 2