LK / Лекция 31

Баранов Виктор Павлович. Дискретная математика. Раздел 6. Конечные автоматы и формальные языки.

Лекция 29. Функциональное описание автомата. автоматы

Лекция 29. ФУНКЦИОНАЛЬНОЕ ОПИСАНИЕ АВТОМАТА

План лекции:

1. Словарные операторы.

2. Словарный оператор, реализуемый автоматом.

3. Минимизация автомата.

Рассмотрим задачу анализа для конечного автомата, которая заключается в установлении функции, реализуемой данным автоматом. Далее мы используем «метод черного ящика», то есть будем рассматривать автомат как преобразователь входных слов в выходные и попытаемся установить какие именно преобразования при этом он выполняет.

1. Словарные операторы

Рассмотрим конечный алфавит , составленный из букв :.

Элементы декартового произведения называют словами длины в алфавите : . При имеем пустое слово, которое обозначается . Множество всех слов в алфавите обозначается : .

Длину слова обозначим . Например, , .

Пусть и – произвольные слова из алфавита . Приписывание слова к слову называется конкатенацией. Полученное при этом слово обозначается : .

Операция конкатенации обладает следующими свойствами:

а) ассоциативность: ;

б) существование нейтрального элемента: .

Очевидно, что эта операция некоммутативна.

Пусть и – два алфавита, и – соответствующие им множества слов. Отображение

называется словарным оператором.

Рассмотрим примеры словарных операторов для двоичных алфавитов .

Пример 1. Оператор сопоставляет каждому слову его первую букву:

.

Пример 2. Оператор производит в слове-аргументе замену каждого нуля на единицу и каждой единицы на нуль:

.

Пример 3. Оператор переписывает каждое слово слева направо:

.

Пример 4. Оператор определяется следующим образом:

,

где

,

,

…

.

2. Словарный оператор, реализуемый автоматом

По определению автомата :

– состояние автомата, в которое он переходит из состояния , когда на его вход поступает символ ;

­ символ на выходе автомата, находящегося в состоянии , в момент, когда на его вход поступает символ .

Обе функции определены на множестве . Расширим область определения до , полагая, что на вход поступает не символ , а слово .

Формальное определение функций и можно дать индуктивно по длине слова.

Базис индукции. Полагаем , .

Индуктивный переход. Предположим, что функции и определены для всех слов , длина которых не превосходит . Рассмотрим произвольное слово длины с первой буквой , то есть . Определим и :

, (1)

. (2)

Из формул (1) и (2) следует, что функции и полностью определяются функциями и , задающими закон функционирования автомата, и являются суперпозициями этих функций. Например, для слова из (1):

.

Из формул (1) и (2) :

,

.

Будем считать, что в момент автомат находится в состоянии , которое будем называть начальным.

Словарным оператором, реализуемым автоматом , называется отображение

,

определяемое следующим образом:

. (3)

Поставим вопрос: каждое ли преобразование слов можно реализовать на автомате? Формально нужно проверить выполнение условия: .

Оказывается, что для выполнения этого условия необходимо, чтобы словарный оператор обладал следующими тремя свойствами.

1. . Следует из (2) и (3).

2. , где . Словарный оператор должен отображать слова с общим началом в слова с общим началом.

Словарный оператор , обладающий свойствами 1 и 2, называется детерминированным.

3. Пусть – детерминированный оператор, а – некоторое слово.

Остаточным оператором оператора , порожденным словом , называется словарный оператор , действующий по правилу:

, если . (4)

Корректность этого определения вытекает из свойства 2. Правило (4) можно сформулировать так: чтобы найти образ слова при отображении , припишем к нему слева слово , найдем образ полученного слова при отображении и удалим в полученном слове букв.

Из определения (4) получим соотношение

. (5)

Действительно, из равенства по определению (4) следует

и .

При . Отсюда получаем (5).

Рассмотрим остаточный оператор для словарного оператора, реализуемого автоматом. Для множества слов, имеющих общее начало , имеем

.

Отсюда

.

Так как – одно из состояний автомата , то

.

Таким образом, – выход автомата, установленного в состояние , на вход которого подано слово . Так число состояний автомата конечно, то получаем свойство 3, согласно которому словарный оператор должен иметь конечное число остаточных операторов.

Словарный оператор, обладающий свойствами 1–3, называется ограниченно-детерминированным.

Мы доказали следующую теорему.

Теорема. Словарный оператор, реализуемый конечным автоматом, является ограниченно-детерминированным.

Справедлива и обратная теорема.

Теорема. Для каждого ограниченно-детерминированного словарного оператора существует реализующий его конечный автомат.

Доказательство. Пусть – ограниченно-детерминированный словарный оператор. Обозначим через число различных остаточных операторов словарного оператора . Если , то – множество всех остаточных операторов словарного оператора (). Поскольку каждый остаточный оператор порождается некоторым словом , разобьем множество всех слов на классов:

, (6)

где . Обозначим класс, в который входит слово через . Имеем

.

Разбиение (6) обладает следующим свойством

. (7)

Построим автомат , реализующий оператор .

Так , то , . В качестве состояний автомата возьмем классы разбиения (6):

. (8)

Функция переходов:

. (9)

Соотношение (9) можно по индукции распространить на слова:

. (10)

Функция выходов:

. (11)

Покажем индукцией по длине слова, что , то есть

. (12)

.

Пусть (12) справедливо для всех слов длины . Рассмотрим произвольное слово длины с последней буквой :

.

По предположению индукции . На основании (10) . Тогда

.

Теорема доказана.

3. Минимизация автомата

Каждый остаточный оператор реализуется в некотором состоянии автомата. Отсюда следует, что у любого автомата , реализующего ограниченно-детерминированный оператор , число состояний не меньше числа различных остаточных операторов оператора :

. (13)

Автомат с наименьшим числом состояний, реализующий ограниченно-детерминированный оператор , называется минимальным автоматом оператора .

Построенный при доказательстве последней теоремы автомат – минимальный.

Теорема. Минимальный автомат единственен с точностью до обозначения состояний.

Из теоремы следует признак минимальности автомата: автомат будет минимальным, если для любых двух его состояний и реализуемые в этих состояниях остаточные операторы различны.

Задача минимизации автомата: для данного автомата построить минимальный автомат, реализующий ограниченно-детерминированный оператор . Рассмотрим алгоритм ее решения.

Пусть . В процессе работы алгоритма строятся разбиения множества на непересекающиеся классы:

.

На очередном шаге алгоритма происходит измельчение предыдущего разбиения до тех пор, пока это возможно. Классы разбиения после завершения алгоритма будут состояниями минимального автомата.

1-й шаг. Состояния и отнесем к одному классу, если

.

Получим разбиение :

.

-й шаг. Пусть на -ом шаге получено разбиение :

.

Состояния и отнесем к одному классу нового разбиения, если выполнены два условия:

1. и 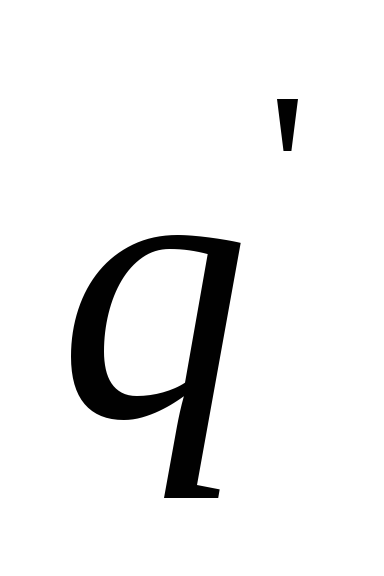входят в один класс предыдущего разбиения ;

2. для каждого символа состояния и 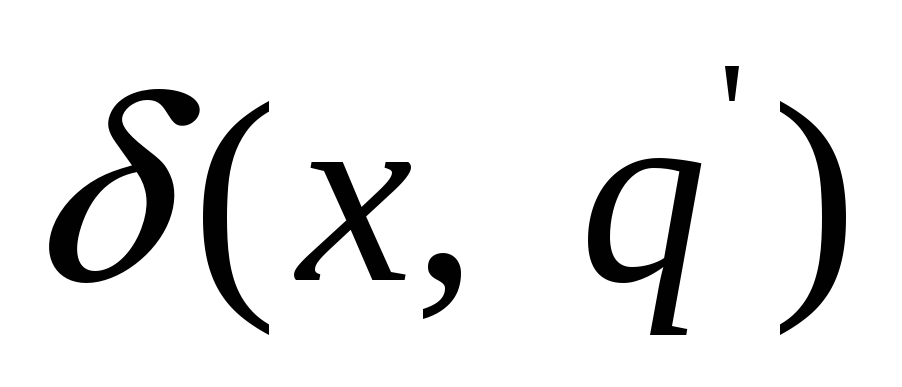входят в один класс предыдущего разбиения .

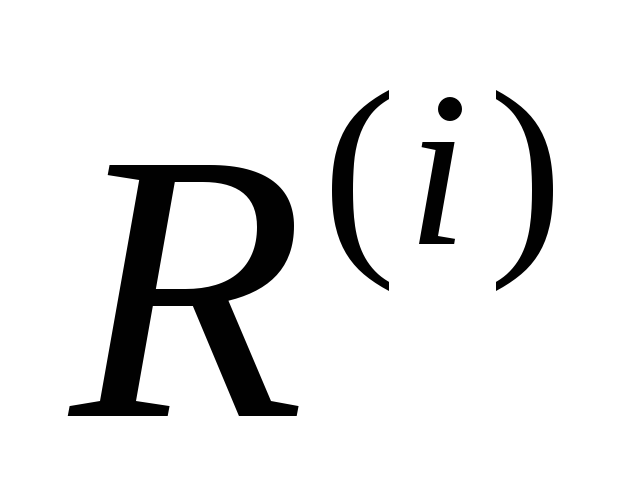Обозначим через класс, в который входит состояние . Тогда условия 1) и 2):

1. ;

2. .

Алгоритм заканчивает работу, когда на некотором шаге не произойдет дальнейшего измельчения разбиения:. Последнее разбиение :

.

Тот факт, что алгоритм закончил работу можно выразить следующим образом:

.

Строим автомат :

, , , , .

Автомат реализует тот же словарный оператор, что и автомат , и является минимальным.

5