

Определенный интеграл. Формула Ньютона Лейбница.
Свойства.
Лекция 4
Определенный интеграл. Задача о площади.
Y•
)
∆ |
x

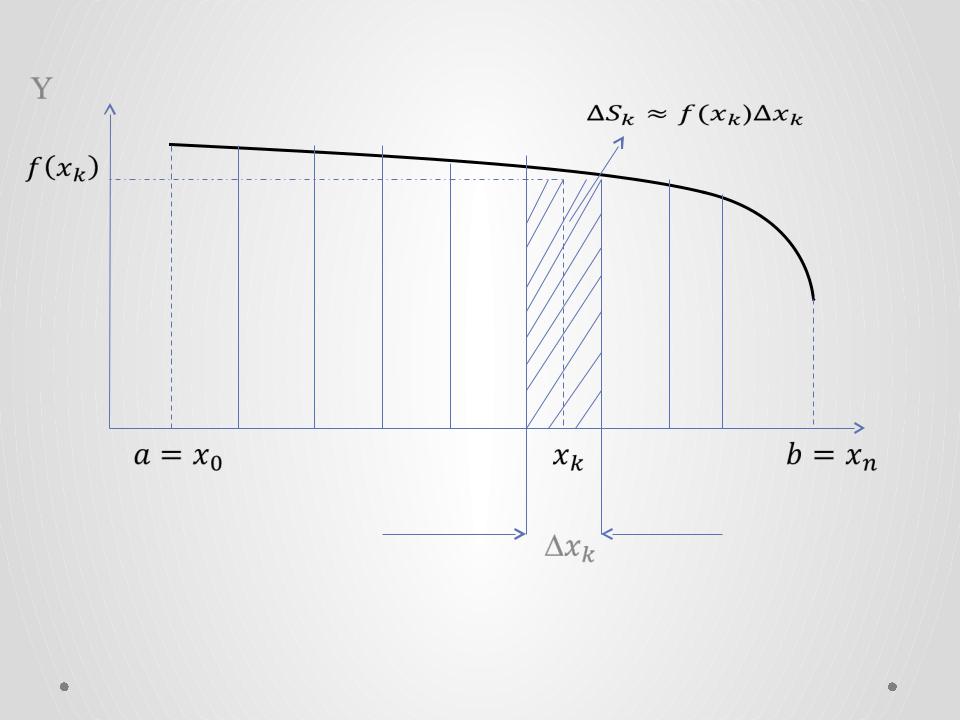
Определенный интеграл. Задача о площади.
Функция• непрерывна на и поэтому имеет следующие свойства:
1.Ограничена на отрезке
2.Принимает на этом отрезке наибольшее и наименьшее значения:
3.Принимает все промежуточные значения между наибольшим
инаименьшим: если ) =
Для вычисления площади разбиваем отрезок на частей шириной . Произвольным образом на каждом интервале выбираем точку вычисляем значение функции Элементарную площадь приближенно представляем как площадь прямоугольника ). А полную площадь представляем как сумму элементарных площадей.

Определенный интеграл. Интегральная сумма.
•= - интегральная сумма.
•Интегральные суммы образуют последовательность:
•………………….
•Определение. Если существует предел последовательности интегральных сумм при условии и этот предел не зависит от способа разбиения на участки и выбора точки , то его называют
определенным интегралом от функции на отрезке
•=
•Геометрический смысл: определенный интеграл – это число, равное площади под графиком функции при условии .
•Если , то
|
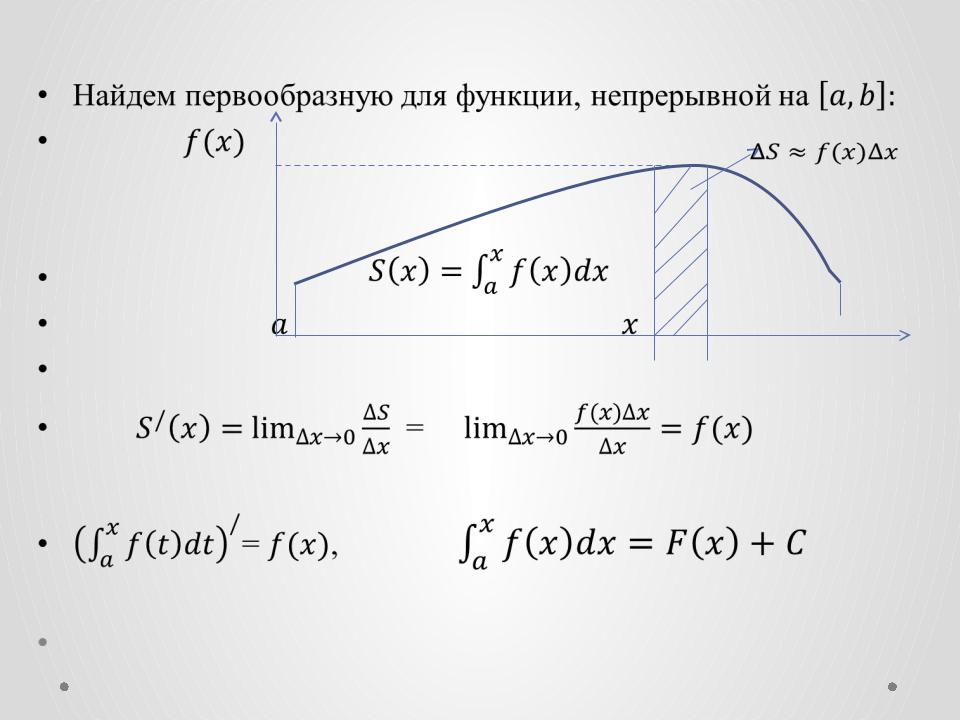
Интеграл с переменным верхним пределом |
• |
Найдем первообразную для функции, непрерывной на |
• |
|
• |
|
• |
|
• |
|
• |
= |
• |
= , |
• |
|

Формула НьютонаЛейбница
•
•Пределы интегрирования – конечные величины
•– непрерывна на
•Пример: )
• Пример: = = = + = ln2
• Площадь.docx

Замена переменной
• Если функция непрерывна на , а функция на где , то
• Пример:
• : соответствует = = 0. соответствует
•= 2 =
•) =

Свойства определенного интеграла
•1. Линейность следует из свойств первообразных и формулы Ньютона – Лейбница:
•2. Аддитивность:
•3.
•4. Свойство знака:
•
•5. Интеграл от нечетной функции на симметричном интервале равен нулю:
•6. Интеграл от четной функции на симметричном
интервале
•

Оценки и приближенное вычисление
•Интегралы бывают «неберущимися», то есть первообразные не могут быть выражены через элементарные функции. Например:
1.Монотонность:,
2.Оценки: где наибольшее и наименьшее значения на отрезке .
3.Теорема о среднем: функция непрерывна на ,
.
Среднее значение функции на интервале интегрирования:
)=
4.Способы приближенного вычисления интегралов при помощи приближенной замены интеграла интегральной суммой (формулы прямоугольников, трапеций и парабол ( метод Симпсона ))выучить самостоятельно.
