Функция нескольких переменных

Лекция 16

Функция нескольких переменных. Определение

Функция• нескольких переменных ─ это закон, по которому группе

упорядоченных действительных чисел ставится в соответствие одно число : .

В случае функции двух переменных каждой паре упорядоченных действительных чисел по определенному правилу ставится в соответствие число: ри этом областью определения называют множество точек плоскости, для которых вычисления по формуле имеют смысл. Графиком функции является поверхность в пространстве.

Примеры:1) для функции + областью определения являются все точки плоскости а графиком является параболоид

Область определения

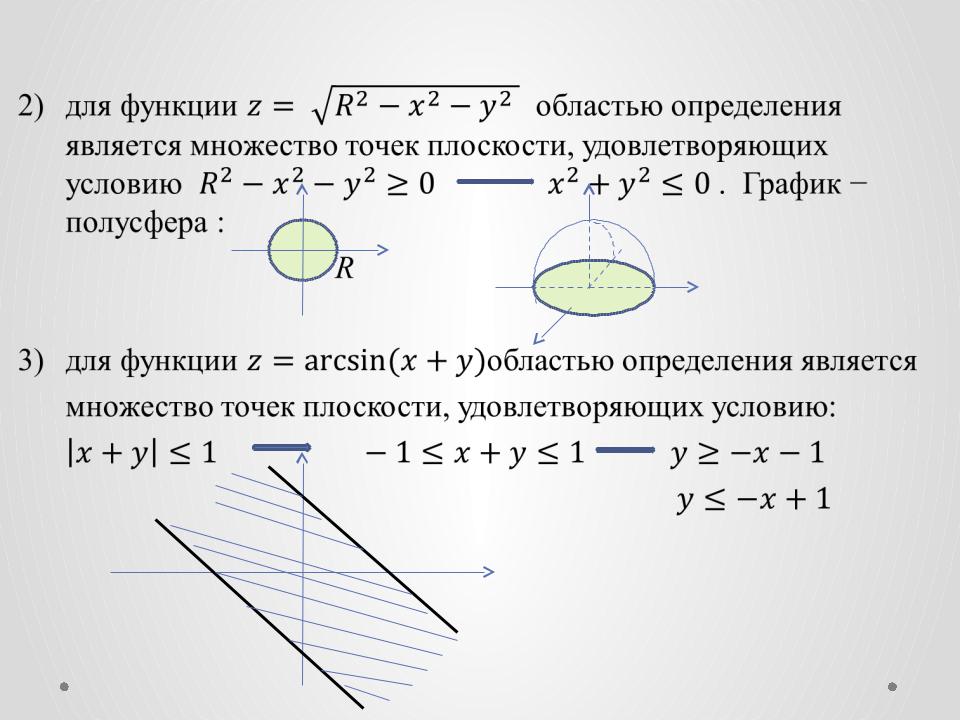
2)• для функции областью определения является множество точек плоскости, удовлетворяющих условию . График − полусфера :

R

3)для функции областью определения множество точек плоскости, удовлетворяющих условию:

1

Виды множеств точек

δ• - окрестность точки задается неравенством

Область − связное открытое множество. Замкнутая область включает точки границы. Ограниченную область можно вписать в круг конечного радиуса.

Замкнутая ограниченная область − аналог понятия отрезок для функции одной переменной.

Понятия линии уровня, предела, непрерывности

Линия• (поверхность) уровня − множество точек, принадлежащих области определения , для которых сохраняется постоянное значение функции.

Пример. Для функции линями уровня являются окружности с центром в начале координат, радиус которых задается постоянным значением z . При − это окружность радиуса

Определение предела: число называют пределом функции при условии , если для любого ε > 0 найдется число δ > 0 такое, что для всех значений из δ – окрестности точки выполняется неравенство .

Предел существует, если он единственный и не зависит от того, по

какой линии . Пример: = = = зависит от углового коэффициента прямой, по которой идет приближение к началу координат, то есть предел не существует

Частные производные первого порядка

•− частное

приращение по переменной − частное приращение по переменной

(– полное приращение

Функция дифференцируема в точке, если в окрестности этой точки полное приращение функции имеет вид:

+

Дифференциал функции – главная , линейная по часть приращения

+,

Единичный вектор направления − приращение функции по направлению .

Производная по направлению или скорость изменения функции в данном направлении:

=

Пример: Найти скорость изменения функции в точке в направлении .

, =,

Градиент

Градиентом• функции в точке называется вектор, координаты которого равны частным производным, взятым в точке. Обозначают

Взаимосвязь градиента и производной по направлению:

Выражение для производной по направлению можно представить как скалярное произведение вектора градиента

и единичного вектора направления или как проекцию градиента на это направление:

Скорость изменения функции максимальна в направлении градиента: φ = 0

Пример: градиент в точке равен Скорость изменения функции в направлении градиента

Касательная плоскость и нормаль к поверхности

нормали к линии (поверхности) уровня, нормаль (нормальный вектор ) в каждой точке поверхности совпадает с направлением градиента:

Уравнение плоскости

Для случая, когда уравнение поверхности