Линейные
дифференциальные уравнения с постоянными коэффициентами
Лекция 6
Линейные дифференциальные уравнения высших порядков с постоянными коэффициентами
•
-постоянные коэффициенты.
–функция, непрерывная на отрезке
Если правая часть уравнения равна нулю то уравнение называют однородным:
0.
Если правая часть уравнения , то уравнение называют
неоднородным.
Уравнение порядка имеет вид
.
Уравнение затухающих колебаний
= 0
Механические колебания
•– смещение
-скорость
– коэффициент упругости пружины
– коэффициент 
трения
Второй закон Ньютона:
Электрические колебания
•
C
L
R
Закон Кирхгофа:
- коэффициент затухания
квадрат частоты собственных - коэффициент затухания колебаний
частоты собственных колебаний
Структура общего решения однородного уравнения
• |
0. |
Совокупность линейно – независимых решений уравнения
образуют фундаментальную систему решений (базис).
Общее решение однородного уравнения записывается как линейная комбинация базисных решений
Решения уравнения подбирают в виде C учетом того, что , ,…… и получают характеристическое уравнение для параметра λ:
+ …… + .
Вид базисных решений определяется видом корней этого характеристического уравнения.
Виды корней многочленов
• |
+ +…… + . |
|||
1. Действительный корень кратности |
, если |
|||
, |
|
|
|
|
Пример: |
|
|
||
2. Действительный корень кратности , |
если |
|||
, |
|
|
|
|
Пример: |
λ = кратности |
|
||
3. Комплексные корни кратности |
|
|||
Вводим мнимую единицу ; |
|
|||
(= 0 |
= |
|
||
Oбозначим |
|
|
||
Пример: |
= ; =1 |
|
||
Общее решение однородного уравнения. Примеры
Уравнению• порядка соответствует
характеристическое уравнение = 0 :
Вид корней |
Базисные |
Общее решение |
Пример |
|
решения |
|
|
D |
; |
|
|
D |
; |
D |
+ |
|
) |
cos
Структура решения неоднородного уравнения
•
Общее решение неоднородного уравнения определяется суммой общего решения соответствующего однородного уравнения ) и какого-либо частного решения неоднородного уравнения
.
Одним из способов нахождения частного решение неоднородного уравнения является подбор по виду правой части специального вида. При этом частное решение в общих чертах повторяет вид правой части. Кроме того, в каждом случае требуется следить за контрольным числом. Если это контрольное число является корнем характеристического уравнения кратности для соответствующего однородного уравнения, то частное решение умножают на 
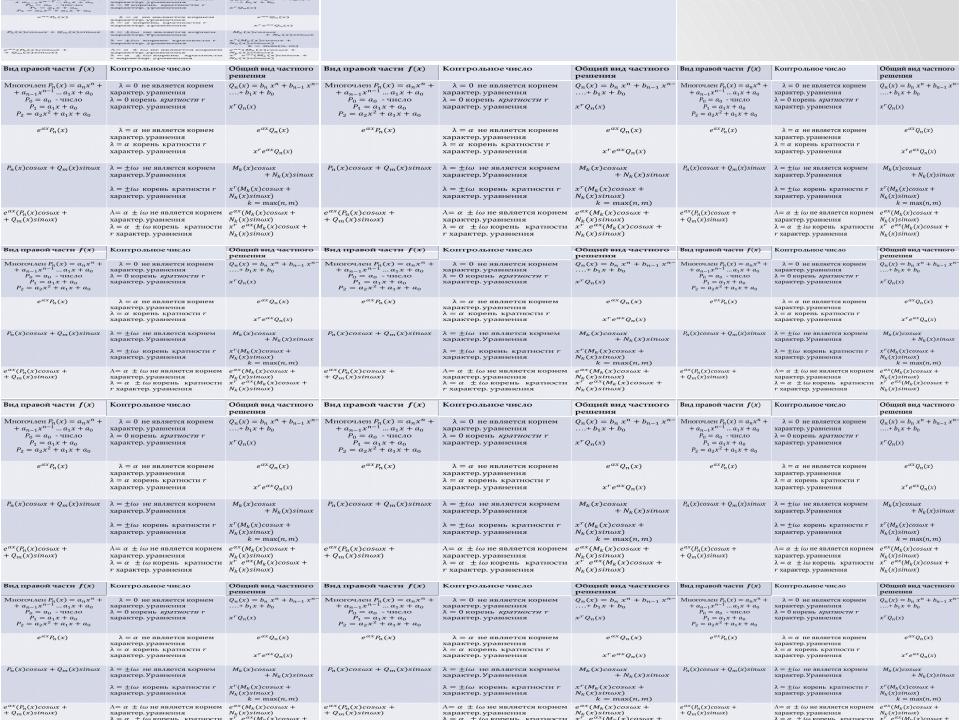
Вид правой части
Многочлен число
Контрольное число |
Общий вид частного |
|
решения |
уравнения |
….+ |
кратности |
|
уравнения |
(x) |
равнения |
|
кратности |
|
уравнения |
(x) |
не является корнем равнения
(
кратности
уравнения
) |
λ |
) |
|
равнения |
( |
|
кратности |
уравнения |
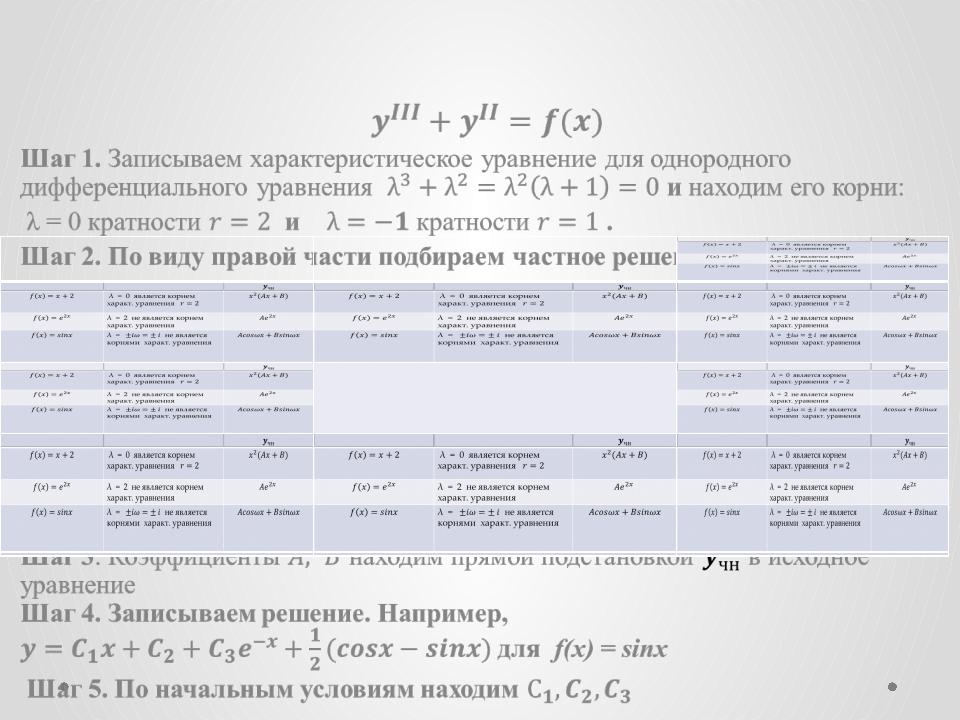
Подбор частного решения по правой части специального вида. Пример.
•
Шаг 1. Записываем характеристическое уравнение для однородного дифференциального уравнения и находим его корни:
λ = 0 кратности и кратности .
Шаг 2. По виду правой части подбираем частное решение:
λ = 0 является корнем характ. уравнения
λ= 2 не является корнем характ. уравнения
λ= не является корнями характ. уравнения
Шаг 3. Коэффициенты находим прямой подстановкой в исходное уравнение
Шаг 4. Записываем решение. Например, для f(x) = sinx
Шаг 5. По начальным условиям находим