Введение в математический анализ: функция , предел, непрерывность
Лекция 1
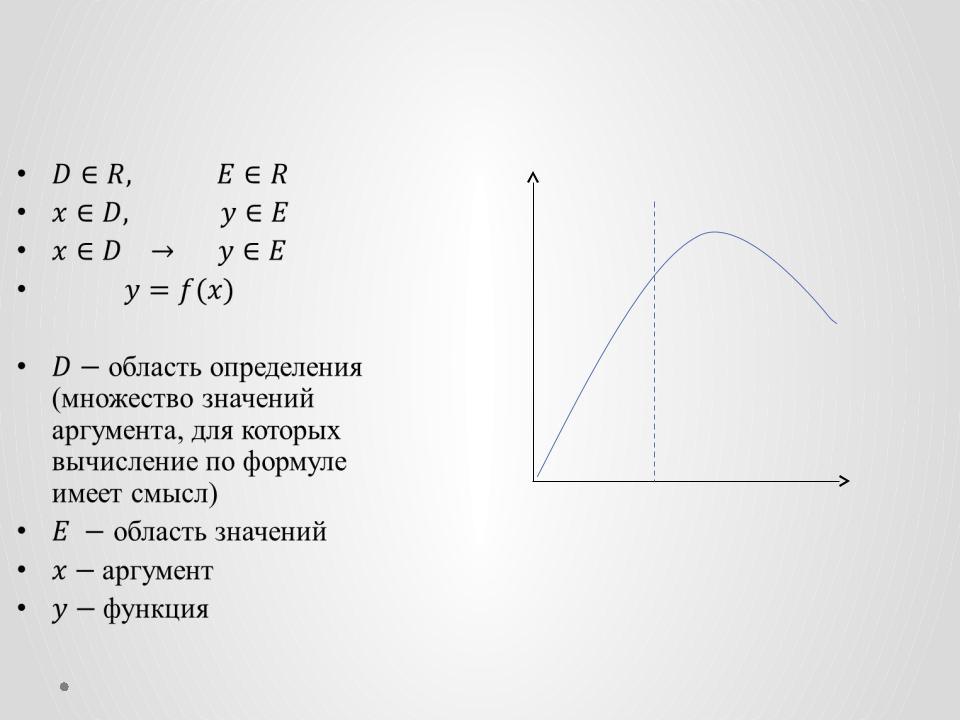
Функция одной действительной независимой переменной
• |
|
y |
• |
|
|
• |
|
|
• |
|
|
• |
область определения |
|
|
(множество значений |
|
|
аргумента, для которых |
|
|
вычисление по формуле имеет |
x |
|
смысл) |
|
|
График функции |
|
• |
область значений |
|
• |
аргумент |
|
• |
функция |
|
2
Основные элементарные функции
•Степенная
•Показательная
•Экспонента
•Логарифмическая (натуральный логарифм, десятичный логарифм)
•Тригонометрические:
•Синус
•Косинус
•Тангенс
•Котангенс
•Литература: Алексеев Д.В. и др. Элементарные аналитические методы и свойства основных элементарных функций. КузГТУ, 1998
•Обратные
тригонометрические функции:
•Арксинус
•Арккосинус
•Арктангенс
•Арккотангенс
•Гиперболические функции: синус, косинус, тангенс, котангенс
•Обратные гиперболические функции: ареасинус, ареакосинус, ареатангенс, ареакотангенс
3
Гиперболические функции
• Основная функция |
• Обратная функция |
• |
• |
• ,
• ,
4
Понятие предела
•Предел последовательности
•Числоназывается пределом
последовательности , если для каждого существует такое натуральное что для любого верно неравенство :
•=
• при
•Примеры:
= 0
Вычисление предела функции по оп ределению.docx
•Предел функции
•Число называется пределом функции в точке (или при если для каждого числа существует такое число , что для всех удовлетворяющих условию выполняется неравенство :
•при
Пример: =8
5
|
Односторонние пределы |
|
|
• |
1. Число называется пределом |
• |
|
|
слева функции в точке (при если |
y |
|
|
для каждого числа существует |
|
|
|
такое число , что для всех |
|
|
|
удовлетворяющих условию |
|
|
|
выполняется неравенство : |
|
|
• |
при - |
|
|
• |
2. Число называется пределом |
|
|
|
справа функции в точке (при |
|
x |
|
если для каждого числа существует |
• |
|
|
такое число , что для всех |
• |
|
|
удовлетворяющих условию |
|
|
|
выполняется неравенство : |
|
|
• |
при + |
|
|
|
|
|
6 |
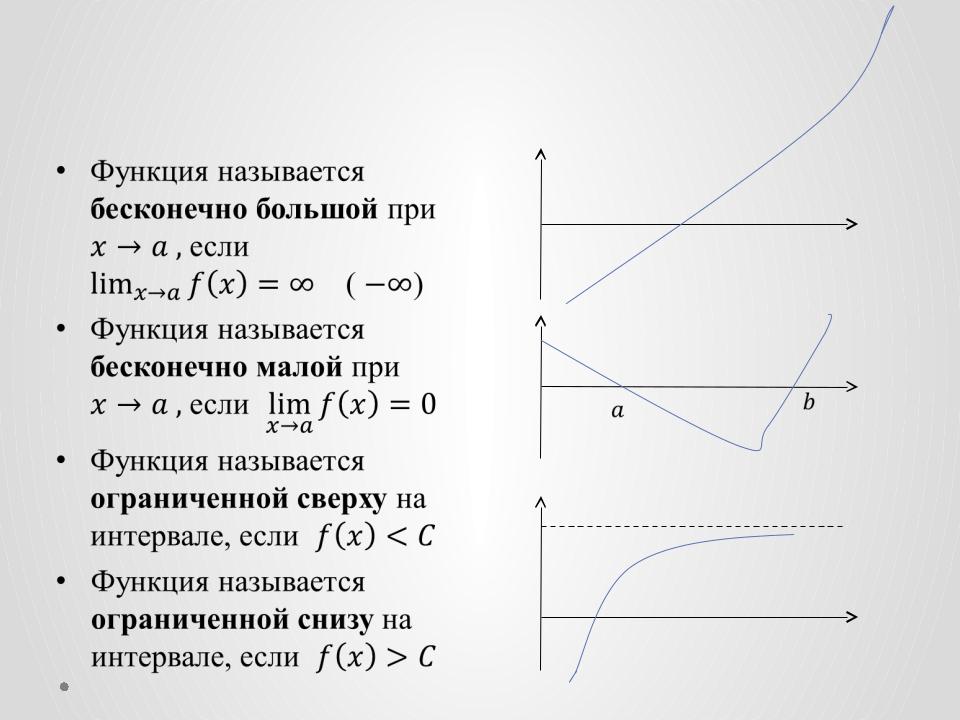
Функции бесконечно большие, бесконечно малые, ограниченные
• |
Функция называется |
|
|
бесконечно большой при |
|
|
если ( ) |
|
• |
Функция называется |
|
|
бесконечно малой при |
|
|
если |
|
• |
Функция называется |
|
|
ограниченной сверху на |
|
|
интервале, если |
|
• |
Функция называется |
С |
|
ограниченной cнизу на |
|
|
интервале, если |
|
7
Действия с бесконечно малыми и бесконечно большими. Неопределенности
1•. Сумма (разность) бесконечно малых функций есть функция бесконечно малая
2.Произведение бесконечно малой и ограниченной функции, а также произведение бесконечно малых есть функция бесконечно малая
3.Произведение бесконечно большой и ограниченной функции, а также произведение бесконечно больших есть бесконечно большая функция
4.Если в окрестности некоторой точки функция является бесконечно большой, то функция является бесконечно малой
5.Если в окрестности некоторой точки функция является бесконечно малой, то функция является бесконечно большой
6.Сумма бесконечно больших одного знака бесконечно большая функция
7.Неопределенности ,, , ,
7. Замечательные пределы.docx
8
Сравнение бесконечно малых |
|
• Определения |
• Обозначения |
1•. Функция называется
бесконечно малой по сравнению с функцией при если =0
2.Функция называется
бесконечно малой одного порядка с функцией при если
=A
3.Функции и называются
эквивалентными бесконечно малыми функциями при если =1
•
Пример: = 0
=
2.
•.,
•.=),
•.3. Пример: =1
9
Эквивалентные бесконечно малые функции при
•
•
10