
Otvety_k_ekzamenu_po_dop_glavam
.pdf
Теории множеств и отношениий
Вопрос №1. Элемент множества, подмножество, пустое и универсальное множества. Операции над множествами и их свойства.
Множеством называется совокупность некоторых элементов, объединенных каким-либо общим признаком.
Элементами множества могут быть числа, фигуры, предметы, понятия и т.п. Совокупность объектов во множестве называется элементами множества. Элементы множеств заключаются в фигурные скобки.
Множество А называется подмножеством множества В, если любой элемент из А является
элементом множества В. (А |
В или В А). |
|
|
}. |
множество, которое не содержит ни одного элемента { |
|
|||
Пустое множество – |
|
определенным свойством, |
||
Универсальное множество — множество, содержащее все элементы с |
|
|
|
|
содержащее в себе все множества, рассматриваемые в задаче. |
|
|
|
|
Операции: |
|
|
|
|
1. Объединением называется множество, содержащее все элементы, принадлежащие либо множеству A, либо B, либо им обоим. Объединение обозначается через A B;
2.Пересечением множеств A и B называется множество, которое обозначается через A ∩ B и содержит элементы, одновременно принадлежащие и множеству A, и множеству В;
3.Разность между множеством A и множеством B состоит из тех элементов первого множества, которые не принадлежат второму, и обозначается через A \ B;
4.Если A и B — и В А, то разность В\А называется дополнением множества А в В и обозначается
5.Симметрической разностью множеств A и B называется множество: A∆B = (A \ B) (B \ A).
Введенные выше операции над множествами обладают следующими свойствами:
Вопрос №2. Равные и равномощные множества, законы алгебры множеств.
Два множества А и В называются равными ( А = В ), если они состоят из одних и тех же элементов, то есть каждый элемент множества А является элементом множества В и наоборот, каждый элемент множества В является элементом множества А .
Два множества называют равномощными, если между ними можно установить взаимно однозначное соответствие, при котором каждому элементу одного множества соответствует ровно один элемент другого. f: A→ B. Понимать это можно так: множества равномощны, если в них одинаковое количество элементов.

Таблица 1. Законы алгебры множеств. |
|
|
1. |
Коммутативность объединения |
1’. Коммутативность пересечения |
2. |
Ассоциативность объединения |
2’. Ассоциативность пересечения |
3. |
Дистрибутивность объединения относительно |
3’. Дистрибутивность пересечения относительно |
пересечения |
объединения |
|
4. |
Законы действия с пустым и универсальным |
4’. Законы действия с пустым и универсальным |
множествами |
множествами |
|
5. |
Закон идемпотентности объединения |
5’. Закон идемпотентности пересечения |
6. |
Закон де Моргана |
6’. Закон де Моргана |
7. |
Закон поглощения |
7’. Закон поглощения |
8. |
Закон склеивания |
8’. Закон склеивания |
9. |
Закон Порецкого |
9’. Закон Порецкого |
 10. Закон двойного дополнения
10. Закон двойного дополнения
Вопрос №3. Булеан, битова строка, характеристические векторы.
Множество всех подмножеств множества 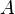 называется булеаном
называется булеаном 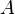 (также степенью множества, показательным множеством или множеством частей) и обозначается
(также степенью множества, показательным множеством или множеством частей) и обозначается 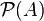 или
или 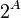 . Ясно, что
. Ясно, что
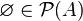 и
и 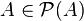 .
.
Множество В состоит из последовательностей нулей и единиц длины n. Они называются строкой бит или битовой строкой длины n.
Пусть S = {s1, s2,... ,sn} причем элементы множества мы пометили числовыми индексами исключительно для удобства ссылок. Если А В , мы поставим ему в соответствие n-битную строку (b1, b2, …, bn), где bi = 1, если si € А и bi = 0 в противном случае. Такая строка бит называется характеристическим вектором подмножества А.
Вопрос №4. Декартово произведение множеств и его мощность. Декартова степень множества.
Если каждому элементу из множества A сопоставлен в соответствие определенный элемент из
множества B, то возникает множество, составленное из пар элементов множеств A и B декартово произведение множеств. Записывают декартово произведение множеств так:
A × B = {(a; b) | a A, b B}.
Мощность декартова произведения равна: |X1 × . . . × Xn| = |X1| · · · · · |Xn|
Произведения вида A×A,A×A×A,A×A×A×A и т.д. принято записывать в виде степени: A2,A3,A4 (основание степени — множество-множитель, показатель — количество произведений). Читают такую

запись как «декартов квадрат» (куб и т.д.). Существуют и другие варианты чтения для основных множеств. К примеру, Rn принято читать как «эр энное».
Вопрос №5. Мощность множества всех подмножеств конечного множества.
Число подмножеств конечного множества, состоящего из 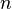 элементов равно
элементов равно 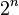 . Доказательство проведем методом математической индукции:
. Доказательство проведем методом математической индукции:
1.База. Если 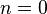 , т. е. множество пусто, то у него только одно подмножество – оно само, и интересующее нас число равно
, т. е. множество пусто, то у него только одно подмножество – оно само, и интересующее нас число равно 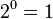 .
.
2.Индукционный шаг. Пусть утверждение справедливо для некоторого n и пусть 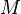 – множество с кардинальным числом
– множество с кардинальным числом 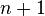 . Зафиксировав некоторый элемент
. Зафиксировав некоторый элемент 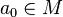 , разделим подмножества множества
, разделим подмножества множества 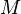 на два типа:
на два типа:
содержащие 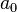 ,
,
не содержащие 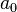 , то есть являющиеся подмножествами множества
, то есть являющиеся подмножествами множества 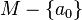 .
.
3.Подмножеств типа (2) по предположению индукции 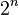 . Но подмножеств типа (1) ровно столько же, так как подмножество типа (1) получается из некоторого и притом единственного подмножества типа (2) добавлением элемента
. Но подмножеств типа (1) ровно столько же, так как подмножество типа (1) получается из некоторого и притом единственного подмножества типа (2) добавлением элемента 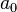 и, следовательно, из каждого подмножества типа (2) получается этим способом одно и только одно подмножество типа (1)
и, следовательно, из каждого подмножества типа (2) получается этим способом одно и только одно подмножество типа (1)
Вопрос №6. Формула включений и исключений для n-множеств.
Формула включений и исключений для n-множеств:
Вопрос №7. Бинарные отношения: способы задания и свойства.
Бинарным отношением между множествами А и В называется подмножество R прямого произведения А х В. В том случае, когда А = В мы говорим просто об отношении R на А. Способ задания бинарного отношения:
1.Матрица бинарного отношения R на множестве Х = {а1, а2,…аn} определяется следующим образом. Порядок матрицы - n, элементы матрицы cij равны:
2. Формула. При составлении отношений с числовыми множествами удобным инструментом их |
|
R | |
|
задания является формула. Например, пусть отношение Q задано следующим образом: Q = {(x,y) |
|
2 |
= |
x2. y = x }, т. е. пара (х,у) для х и у, являющихся действительными числами, связана отношением y |
|
Свойства бинарных отношений
Отношение называется рефлексивным, если каждый элемент x A находится в этом отношении сам с собой: x x для всех x A;
Отношение называется симметричным, если из того, что x y , следует, что y x;
Отношение называется транзитивным, если из того, что x y и y z, следует, что x z;
Нерефлексивным
Несимметричным;
Нетранзитивным;
Антирефлексивным;

Антисимметричным;
Антитранзитивным.
Вопрос №8. Отношение эквивалентности и теорема о разбиении множества на классы эквивалетности.
Отношение эквивалентности. Некоторые х Х можно рассматривать в определенных случаях как эквивалентные, т.е. когда любой из этих элементов может быть заменен на другой из этого же множества. Например, «числа, делящиеся на 2» или «быть студентом группы №222» и т. д. Отношение эквивалентности обозначается символом «º».
Свойства отношений эквивалентности:
1.Рефлексивность;
2.Симметричность;
3.Транзитивность.
Таким образом, отношение называется отношением эквивалентности, если оно рефлексивно, симметрично и транзитивно.
Теорема: каждое отношение эквивалентности, определенное на А, соответствует некоторому разбиению множества А. Всякое разбиение множества А соответствует некоторому отношению эквивалентности на множестве А.
Коротко: между классами всех определенных на множестве А отношений эквивалентностей и классом всех разбиений множества А существует взаимнооднозначное соответствие.
Вопрос №9. Кольцо вычетов по модулю 3.
Вопрос №10. Отношения частичного и линейного порядков. Диаграмма Хассе.
Рефлексивное, транзитивное, но кососимметричное отношение R на множестве А называется частичным порядком. Множества с частичным порядком принято называть частично упорядоченными множествами. Линейным порядком на множестве А называется отношение частичного порядка, при котором из любой пары элементов можно выделить предшествующий и последующий.
Непосредственных предшественников можно условно изобразить с помощью графа, известного как
диаграмма Хассе.
Вопрос №11. Отношения «k делитель n» и «А подмножество В».
Функции
Вопрос №1. Обратное отношение, композиция отношений, матрица композиций отношений.
Обратным к P отношением является множество P -1 = { (y, х) : (x,y) € P }, т. е. P -1 связывает те же пары элементов, что и отношение P, но в другом порядке.
Композицией R и S называется бинарное отношение между A и С, которое обозначается
S о R и определяется формулой: S о R = {(а, с): а € А, с € С и aRc, bSс для некоторого b € В}. Композиция - это применение одной функции к результату другой. Новое отношение устанавливает связь между элементами множеств А и С, используя элементы из В в качестве посредников.
Композицию бинарных отношений можно вычислить и с помощью матриц, их определяющих. Имея матрицы двух отношений, мы построим матрицу их композиции. Она называется логическим или булевым произведением матриц. Матрица отношения R строится:
М(i, j) = И если (аi, bj) € R, M{i, j) = Л если (аi, bj) € R.
Матрица отношения S строится:
N(i, j) = И если (bi, cj) € S,

N(i, j) = Л если (bi, cj) € S.
Матрица композиции строится:
Р(i, j) = [М(i, 1) и N(1, j)] или [М(i, 2) и N(2, j)]… или [М(i, n) и N(n, j)].
Вопрос №2. Функция на множестве А, область определения функции, множество значений функции, инъекция, сюръекция и биекция.
Функцией из множества А в множество В называется бинарное отношение, при котором каждый элемент множества А связан с единственным элементом множества В. В графических терминах функция описывается таким графом, у которого из каждой вершины, изображающей элементы множества
A, выходит ровно одна стрелка.
Область определения функции — множество, на котором задаётся функция f : А → B Множеством значений функции f называется подмножество в B, состоявшее из образов всех
элементов a € А. Оно обозначается символом f(A) и формально определяется так: f(А) = { f(x) : х € А}.
Инъекцией или взаимно однозначной функцией называется функция если:
F(a1) = f(a1) = a1=a2 для всех a1,a2 € А.
Функция сюръективна, если множество ее значений совпадает с областью значений. Это означает, что для каждого b € В найдется такой
а € А что b = f(a).
Функция биективна, если она как инъективна, так и сюръективна.
Вопрос №3. Обратимая и обратная функция, необходимое и достаточное условие обратимости функции.
Обратимая функция — это функция, которая принимает каждое своё значение в единственной точке области определения.
Обратная функция — функция, обращающая зависимость, выражаемую данной функцией. Например, если функция от x даёт y, то обратная ей функция от y даёт x.
Функция обратима тогда и только тогда, когда она биективна.
Вопрос №4. Принцип Дирихле. Обобщённый принцип Дирихле.
Принцип Дирихле гласит, что если |А| > |В|, то по крайней мере одно значение встретится более одного раза. Проще говоря, найдется пара элементов аi ≠ aj для которых f(аi) = f(aj).
Принцип можно обобщить следующим образом. Рассмотрим функцию f : А → B, где А и В — конечные множества. Если |А| > k|В| для некоторого натурального числа k, то найдется такое значение функции f, которое она будет принимать, по крайней мере, (k + 1) раз.
Комбинаторика
Вопрос №1. Правило суммы, правило произведения, правило взаимно-однозначного соответствия.
Правило суммы гласит, что если А и В — несвязанные события, и существует n1 возможных исходов события A, и n2 возможных исходов события B, то возможное число исходов события
«А или B» равно сумме n1+n2.
Правило произведения утверждает, что если дана последовательность k событий с n1 возможными исходами первого, n2 — второго, и т. д., вплоть до nk возможных исходов последнего, то общее
число исходов последовательности k событий равно произведению n1+n2 + … + nk.

Правило взаимно однозначного соответствия (правило биекции или правило равенства): множества A и B имеют одинаковое количество элементов | A | = | B | тогда и только тогда, когда между ними можно установить взаимно однозначное соответствие.
Вопрос №2. Вывести формулу числа всех (n,k)-размещения и (n,k)-сочетания с повторением элементов.
(n,k)-размещений с повторениями. На первое место выборки мы можем поставить любой из п элементов множества. Поскольку повторения разрешены, то на второе место мы опять можем поставить любой элемент из этого же множества, и т. д. Поскольку у нас k мест в
выборке, то опираясь на правило произведения, получаем, что число всех (n,k)-размещений с повторениями равно nk.
Возвращаясь к общему случаю (n,k)-сочетаний с повторениями (k объектов из n данных), заметим, что нам потребуется n - 1 метка и k объектов. Таким образом, у нас будет {п — 1) + k ячеек для заполнения. Значит, число (n,k)-сочетаний без повторений совпадает
с количеством способов размещения (n - 1) метки в (n + k - 1) ячейку. Итак, общее число (n,k)-сочетаний без повторений равно:
Вопрос №3. Вывести формулу числа всех (n,k)-размещения и (n,k)-сочетания без повторения элементов.
Для числа всех (n,k)-размещений без повторений зафиксировано специальное обозначение (n,k).Подсчитаем это число. На первое место выборки мы можем поставить любой из n элементов. Поскольку здесь нам не разрешены повторения, то для второго места мы можем выбрать любой из (n - 1) оставшихся элементов. На третье - из (n - 2) и так далее, вплоть до k-го места, куда можно написать любой из (n – k +1) элементов. Теперь для окончательного ответа нам нужно применить правило произведения. Имеем:
A |
A 
Таким образом, на каждое (n,k)-сочетание без повторений приходится k! различных (n,k)- размещений без повторений. Стало быть,
Вопрос №4. Сочетания с повторением элементов. Задача про садовника. Задача о числе целочисленных решений уравнения a + b + c + … + z = n.
Вопрос №5. Задача о числе счастливых билетов.
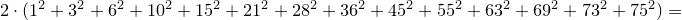
Само решение требует достаточно большого числа вычислений, однако они не очень сложные. Важно понять, как их сократить.
Найдем 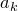 — число билетов, у которых сумма первых трех цифр равна сумме трех последних цифр и равна
— число билетов, у которых сумма первых трех цифр равна сумме трех последних цифр и равна 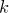 . Ясно, что
. Ясно, что 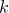 может принимать значения от
может принимать значения от 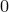 (три
(три 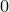 ) до
) до 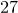 (три “девятки’’).
(три “девятки’’).
Сначала докажем, что 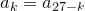 . В самом деле, каждой последовательности из трех десятичных цифр с суммой цифр
. В самом деле, каждой последовательности из трех десятичных цифр с суммой цифр 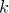 от
от 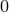 до
до 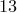 можно поставить в соответствие последовательность из трех десятичных цифр с суммой цифр
можно поставить в соответствие последовательность из трех десятичных цифр с суммой цифр 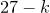 следующим образом: каждую цифру
следующим образом: каждую цифру в исходной последовательности заменим на цифру
в исходной последовательности заменим на цифру 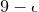 . Тем самым, каждой последовательности из трех десятичных цифр с суммой цифр
. Тем самым, каждой последовательности из трех десятичных цифр с суммой цифр 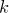 от
от 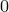 до
до 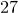 будет соответствовать одна и только одна последовательность из трех десятичных цифр с суммой цифр
будет соответствовать одна и только одна последовательность из трех десятичных цифр с суммой цифр 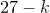 , принимающей значения от
, принимающей значения от 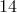 до
до 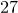 . Значит, таких последовательностей с суммой цифр
. Значит, таких последовательностей с суммой цифр 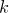 , где
, где 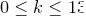 столько же, сколько последовательностей с суммой цифр
столько же, сколько последовательностей с суммой цифр 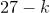 (
(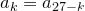 ).
).
Далее нам понадобится число способов представления целого неотрицательного числа 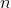 в виде
в виде
суммы трех целых неотрицательных слагаемых. Это можно сделать 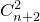 способами. Действительно, число способов равно числу сочетаний с повторениями из
способами. Действительно, число способов равно числу сочетаний с повторениями из 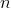 по
по 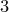 (или иначе, разбиваем
(или иначе, разбиваем 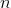 единиц на три группы — три слагаемых, в качестве разделителей используем нули, всего
единиц на три группы — три слагаемых, в качестве разделителей используем нули, всего 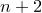 элемента, из которых нужно выбрать
элемента, из которых нужно выбрать 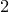 нуля, см. сочетания с повторениями).
нуля, см. сочетания с повторениями).
Число способов 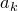 получить сумму
получить сумму 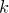 от
от 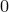 до
до 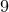 можно вычислить по полученной формуле:
можно вычислить по полученной формуле: 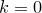 :
: 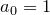 (впрочем, это и так очевидно,
(впрочем, это и так очевидно, 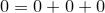 , иначе никак),
, иначе никак),
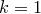 :
: 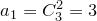 ,
,
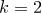 :
: 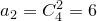 ,
,
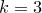 :
: 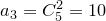 ,
,
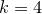 :
: 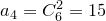 ,
,
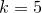 :
: 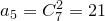 ,
,
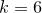 :
: 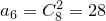 ,
,
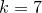 :
: 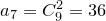 ,
,
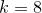 :
: 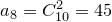 ,
,
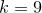 :
: 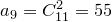 .
.
Теперь перейдем к  . Здесь все немного сложнее, потому что цифры
. Здесь все немного сложнее, потому что цифры  не существует, и нам нужно из всех способов разбиения числа
не существует, и нам нужно из всех способов разбиения числа 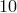 не три целых неотрицательных слагаемых вычесть те способы, в которых одно из слагаемых равно
не три целых неотрицательных слагаемых вычесть те способы, в которых одно из слагаемых равно 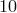 . Подсчитать эти способы можно довольно легко. Мы первое слагаемое в разложении числа
. Подсчитать эти способы можно довольно легко. Мы первое слагаемое в разложении числа 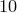 на сумму трех слагаемых положим равным
на сумму трех слагаемых положим равным 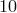 , а дальше подсчитаем количество способов представить оставшееся число (
, а дальше подсчитаем количество способов представить оставшееся число (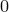 ) в виде суммы трех целых неотрицательных
) в виде суммы трех целых неотрицательных
слагаемых (этих способов 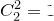 ). Получаем (с учетом того, что слагаемое
). Получаем (с учетом того, что слагаемое 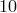 может стоять на трех разных местах)
может стоять на трех разных местах)
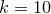 :
: 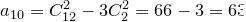 .
.
Для 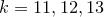 поступаем точно так же. Сначала находим число способов представить
поступаем точно так же. Сначала находим число способов представить 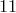 в виде суммы трех целых неотрицательных слагаемых — оно равно
в виде суммы трех целых неотрицательных слагаемых — оно равно 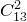 , а затем вычитаем те способы, в которых одно из слагаемых больше либо равно десяти — их всего
, а затем вычитаем те способы, в которых одно из слагаемых больше либо равно десяти — их всего 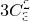 . Итак,
. Итак, 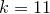 :
: 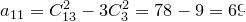 ,
, 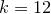 :
: 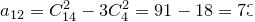 ,
,
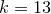 :
: 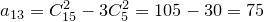 .
.
Число билетов, у которых сумма первых трех цифр равна сумме последних трех цифр и равна 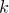 ,
,
находится как 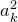 (независимо от способа выбора первых трех цифр с суммой
(независимо от способа выбора первых трех цифр с суммой 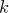 мы можем выбрать три последние цифры, сумма которых также равна
мы можем выбрать три последние цифры, сумма которых также равна 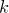 ).
).
Осталось найти общую сумму:
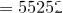 .
.
Итак, всего есть 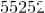 “счастливых’’ билета.
“счастливых’’ билета.

Вопрос №6. Перестановки без повторения и с повторением элементов.
Фактически, нам нужно подсчитать количество (k,k)-размещений без повторений:
С повторениями:
Вопрос №7. Разбиения множества на части (упорядоченные и неупорядоченные).
Неупорядоченное разбиение n -элементного множества X— это любое семейство {X1, X2,…, Xk}, где 1 ≤ k ≤n; X1, X2,…,Xk - непустые попарно непересекающиеся подмножества множества X , объединение которых равно X.
Называем такое разбиение неупорядоченным, так как семейство — это неупорядоченная совокупность.
Упорядоченным разбиением конечного множества X с n-элементами называется любой кортеж вида <X1, X2,…,Xk>, где 1 ≤k ≤ n; X1, X2,…,Xk - непустые попарно непересекающиеся, подмножества множества X, объединение которых равно X. Называем такое разбиение упорядоченным, так как элементы кортежа упорядочены.
Вопрос №8. Свойства чисел сочетаний Cnk , бином Ньютона.
Свойства чисел:
1.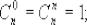
2.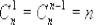
3.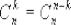 ;
;
4.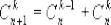 ;
;
5.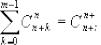 , (m 1);
, (m 1);
Числа С(n, к) возникают как коэффициенты при раскрытии скобок в биноме (а + b)n. Например,
Эта формула называется биномом Ньютона. Ровно поэтому коэффициенты С(n, к) часто называют биномиальными коэффициентами. Биномиальные коэффициенты полезно выстроить в так называемый треугольник Паскаля

Вопрос №9. Мультиномиальные коэффициенты.
Мультиномиальные (полиномиальные) коэффициенты — коэффициенты в 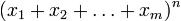 разложении
разложении 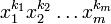 по мономам :
по мономам :
Группы, кольца, поля
Вопрос №1. Группа, кольцо, поле. Примеры числовых групп, колец, полей.
Множество 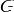 с алгебраической операцией
с алгебраической операцией  называется группой, если выполняются следующие условия:
называется группой, если выполняются следующие условия:
1.Операция  в
в 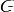 ассоциативна:
ассоциативна: 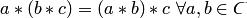 ;
;
2.В 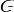 существует нейтральный элемент
существует нейтральный элемент 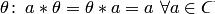 ;
;
3.для каждого элемента 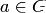 существует обратный ему элемент
существует обратный ему элемент
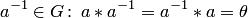 . Примеры групп:
. Примеры групп:
Все целые, все рациональные, все действительные и все комплексные числа являются группами относительно операции сложения чисел, играющего роль групповой операции умножения;
Все рациональные, все действительные и все комплексные числа, исключая число 0, являются
группами относительно операции умножения чисел.
Если операция  коммутативна, то группа называется коммутативной, или абелевой. В противном случае группа называется некоммутативной.
коммутативна, то группа называется коммутативной, или абелевой. В противном случае группа называется некоммутативной.
Множество 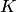 , на котором заданы две операции — сложение
, на котором заданы две операции — сложение 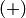 и умножение
и умножение 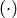 , называется кольцом, если выполняются следующие условия:
, называется кольцом, если выполняются следующие условия:
1.Относительно операции сложения множество 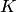 — коммутативная группа, т.е.
— коммутативная группа, т.е.
операция сложения коммутативна: 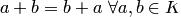 ;
;
операция сложения ассоциативна: 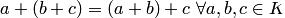 ;
;
существует нулевой элемент 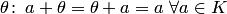 ;
;
для каждого элемента 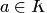 существует противоположный ему элемент
существует противоположный ему элемент 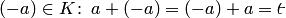 ;
;
2.Операция умножения во множестве 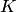 ассоциативна;
ассоциативна;
3.Операции сложения и умножения связаны законами дистрибутивности.

Если операция умножения коммутативна: 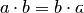 , то кольцо называется коммутативным, в противном случае кольцо называется некоммутативным. Если для операции умножения существует единичный элемент
, то кольцо называется коммутативным, в противном случае кольцо называется некоммутативным. Если для операции умножения существует единичный элемент  , то говорят, что кольцо
, то говорят, что кольцо 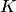 — есть кольцо с единицей.
— есть кольцо с единицей.
Примеры колец при обычных операциях сложения и умножения кольцом является:
1.Множество целых чисел;
2.Множество рациональных чисел;
3.Множество действительных чисел;
4.Множество рациональных чисел;
5.Множество, состоящее лишь из одного числа 0;
6.Множество четных чисел и вообще множество целых чисел, кратных некоторому числу n;
7.Множество комплексных чисел a + bi с целыми a и b (так называемое кольцо целых комплексных чисел).
Множество 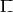 , на котором заданы две операции: сложение
, на котором заданы две операции: сложение 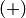 и умножение
и умножение 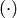 , называется полем, если выполняются следующие условия:
, называется полем, если выполняются следующие условия:
1.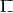 — коммутативное кольцо с единицей
— коммутативное кольцо с единицей 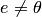 ;
;
2.Для каждого элемента 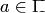 , отличного от нулевого
, отличного от нулевого 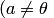 , существует обратный элемент
, существует обратный элемент
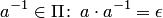 .
.
Поле — это множество, в котором определены четыре операции: сложение, умножение, вычитание и деление. Полями, например, являются множества рациональных и действительных чисел.
Примеры полей:
1.Множество комплексных чисел a + bi с любыми рациональными a, b;
2.Множество всех рациональных функций с действительными коэффициентами от одного или нескольких переменных;
3.Множество из двух элементов, которые обозначим через 0 и 1, при следующем определении операций:
Вопрос №2. Группа подстановок (биекций), циклическая запись подстановок, циклическая группа.
Множество всех подстановок множества X (т.е. биекций X →X) с операцией композиции образуют группу, которая называется симметрической группой или группой подстановок X.
Обычно обозначается S(X). Если X = {1, 2,..., n}, то S(X) обозначается через Sn.
Подстановки удобно записывать в циклической форме. При такой записи индексы, остающиеся на месте, обычно не пишутся. Так, подстановка a имеет следующие переходы индексов: 0 → 0, 1 → 4 → 2 → 1, 3 → 3, 5 → 6 → 5. Следовательно, в циклической форме она запишется следующим образом:
а = = (0)(142)(3)(56) = (0)(142)(3)(56)(7)(8)... = (142)(56).
Группа 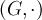 называется циклической, если существует такой элемент
называется циклической, если существует такой элемент 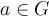 , что любой элемент
, что любой элемент
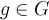 записывается в виде
записывается в виде 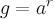 для некоторого
для некоторого 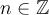 . При этом элемент
. При этом элемент 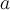 называется образующей циклической группы.
называется образующей циклической группы.
Вопрос №3. Действие группы на множестве, орбита элемента, подгруппа, теорема Лагранжа о порядке подгруппы.
Группа 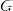 действует на
действует на 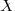 , если любых
, если любых 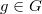 и
и 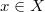 определено действие элемента
определено действие элемента 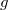 на элемент
на элемент  (обозначаемое
(обозначаемое 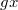 ), обладающее следующими свойствами:
), обладающее следующими свойствами:
1.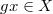 ,
,
2.Для любых 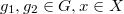 выполнено
выполнено 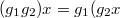 ,
,
3.Для любого 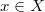 выполнено
выполнено 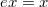 .
.
Действие группы:
