
Otvety_k_ekzamenu_po_dop_glavam
.pdf
Действие группы на себя. Пусть 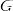 — группа с операцией и множество
— группа с операцией и множество  . Зададим отображение
. Зададим отображение  , такое что
, такое что 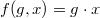 . Тогда все свойства из определения выполнятся вследствие соответствующих свойств группы. Таким образом группа
. Тогда все свойства из определения выполнятся вследствие соответствующих свойств группы. Таким образом группа 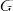 действует на
действует на  . Такое действие называется "действие левыми сдвигами".
. Такое действие называется "действие левыми сдвигами".
Действие сопряжением. Пусть  — группа с операцией и множество
— группа с операцией и множество 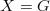 . Зададим отображение
. Зададим отображение  , такое что
, такое что  . Все свойства из определения выполнены, следовательно группа
. Все свойства из определения выполнены, следовательно группа 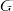 действует на
действует на 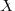 .
.
X под действием G называется множество Gx = {gx | g G}. Количество
элементов в данной орбите называется длиной орбиты (в разных орбитах может быть разное количество элементов). Любые две орбиты либо не пересекаются, либо совпадают. Таким образом, множество X разбивается в дизъюнктное объединение орбит
Подгруппа ― подмножество 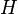 группы
группы  , само являющееся группой относительно операции, определяющей
, само являющееся группой относительно операции, определяющей  .
.
Подмножество 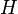 группы
группы  является её подгруппой тогда и только тогда, когда:
является её подгруппой тогда и только тогда, когда:
содержит произведение любых двух элементов из 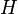 ,
,
содержит вместе со всяким своим элементом 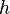 обратный к нему элемент
обратный к нему элемент  .
.
В случае конечных и, вообще, периодических групп проверка условия 2 является излишней. Теорема Лагранжа: В конечных группах порядок любой подгруппы делит порядок группы
Вопрос №4. Формула (лемма) Бернсайда о числе орбит.
Количество орбит действия группы G на множестве X равно:
Вопрос №5. Задача о числе раскрасок вершин правильного многогранника (куба, тетраэдра, октаэдра). Вопрос №6. Кольца и поля вычетов, решение уравнений в кольцах и полях вычетов.
Вопрос №7. Обратимые элементы в поле и кольце вычетов, формула Эйлера для числа взаимопростых чисел с данным числом.
Обратимым элементом, а также единицей кольца или делителем единицы, называется всякий элемент a кольца, для которого существует обратный элемент относительно умножения, то есть такой
элемент b, что ab = ba = e, где e — единичный элемент кольца.
Логика и доказательство
Вопрос №1. Формы мышления, объём и содержания понятий. Закон обратного отношения. Отношения между объёмами понятий.
Форма мышления – это способ, которым мы выражаем (фиксируем) наши мысли, или схема, по которой они строятся. Существует всего три формы мышления: понятие, суждение и умозаключение. Каждое понятие имеет содержание и объем.
Содержание понятия – это совокупность существенных признаков, отраженных в данном понятии. Объем понятия – это множество предметов, которые имеют эти существенные признаки. Существует обратная зависимость: чем больше объем понятия, тем меньше его содержание и
наоборот.
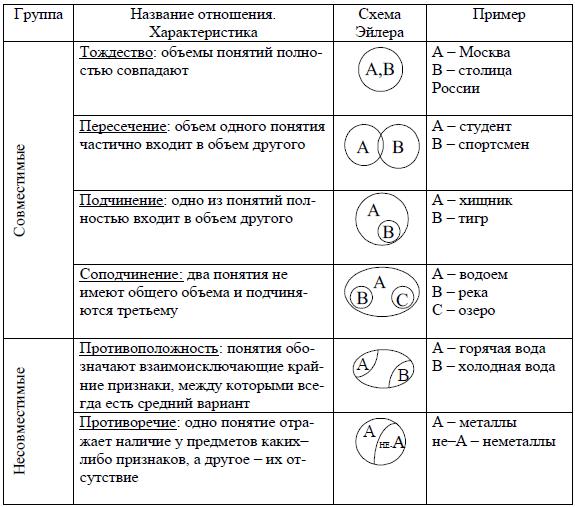
Понятия бывают сравнимые («город» и «населенный пункт», «спортсмен» и «россиянин») и несравнимые («романс» и «кирпич», «истина» и «нитка»).
Вопрос № 2. Форма суждения. Субъект и предикат суждения, кванторы и логические связки. Логическое значение суждения.
Суждение – форма мышления, в которой что–либо утверждается или отрицается о предметах, их свойствах или отношениях между ними.
Суждение характеризуется содержанием и формой.
Содержание суждения – это то, о чем в нем идет речь, его смысл.
Логическая форма суждения – его строение, способ связи его составных частей.
В суждении выделяют субъект S (логическое подлежащее) – это понятие, о котором идет речь в суждении; предикат P (логическое сказуемое) – это понятие, с помощью которого что–либо утверждается или отрицается о субъекте и связку – слова есть, является, называется (часто отсутствует).
Простым называется суждение, в котором присутствуют только один субъект и один предикат. Суждение называется сложным, если оно образовано из простых с помощью логических операций
(связок).
По качеству простые суждения делятся на утвердительные (связка есть) и отрицательные (связка не
есть).
Пример 1. Дано суждение "Земля является планетой".
В нем субъект S – "Земля", предикат P – " планета", связка – слово "является". Следовательно, суждение простое, утвердительное.
Количественная характеристика суждений передается с помощью кванторов. Единичные суждения относятся к общим.
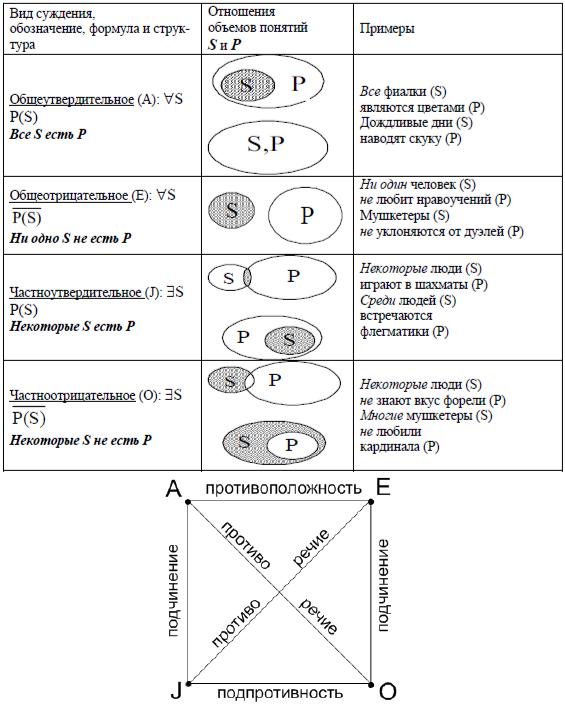
Вопрос №3. Классификация суждений-высказываний по количеству и качеству, логический квадрат.
По количеству суждения делятся на общие, частные. Количество определяется объемом субъекта суждения. Объем субъекта может быть пол ным (все, ни один) или частичным (некоторые).
Простое суждение можно записать в виде формулы. Количественная характеристика суждений передается с помощью кванторов. Единичные суждения относятся к общим.
Классификация простых суждений:
Вопрос №4. Форма умозаключения. Разновидности умозаключений. Правильность умозаключений.
Умозаключение – форма мышления, в которой из одного или нескольких суждений (называемых посылками) выводится новое суждение – заключение (вывод).

По составу все умозаключения делятся на простые и сложные. Простыми называются умозаключения, элементы которых не являются умозаключениями. Сложными называют умозаключения, состоящие из двух или более простых умозаключений.
По количеству посылок умозаключения делятся на непосредственные (из одной посылки) и опосредованные (из двух и более посылок).
Дедуктивное умозаключение - умозаключение, в котором переход от общего знания к частному является логически необходимым. Путем дедукции получаются достоверные выводы: если истинны посылки, то будут истинны и заключения.
Индуктивное умозаключение - умозаключение, в котором переход от частного знания к общему осуществляется с большей или меньшей степенью правдоподобности (вероятности).
Рассмотрим умозаключения, содержащие две и более посылок. Умозаключение является логически правильным, если из истинности всех его посылок следует истинность заключения.
Умозаключение логически неправильно, если при истинности всех его посылок заключение может быть как истинным, так и ложным.
Правильность умозаключения проверяется с помощью таблиц истинности или, в том случае если посылок много, индуктивным методом.
Общая схема проверки Запишем формулу каждой Посылки (П) и Заключения:
Оформим задачу в виде схемы
Запишем конъюнкцию посылок Посылка 1 ^ Посылка 2.
Строим таблицу истинности.
Исследуем строки, где Посылка 1 ^ Посылка 2 = 1. Если во всех этих строках Заключение = 1, то умозаключение логически правильно. Если встречается строка, в которой Заключение = 0, то умозаключение логически неправильно.
Вопрос №5. Виды непосредственных умозаключений
Виды непосредственных умозаключений:
Превращение.
Обращение.
Противопоставление предикату.
Покажем преобразования суждений каждого логического вида на конкретных примерах. Для каждого суждения запишем формулу, определим понятия соответствующие субъекту (S) и предикату (P)
1.«Все фиалки являются цветами» (А), ) S( P S; S – «быть фиалкой», P – «те, кто является цветком».
2.«Никто из мушкетеров не уклонялся от дуэлей» (Е), SP(S) ; S – «быть мушкетером», P – «те, кто
уклоняется от дуэлей».
Превращение – операция, при которой изменяется качество посылки, без изменения ее количества. Осуществляется двумя способами:
1.используя двойное отрицание, которое ставится перед связкой и перед предикатом: S есть P → S не
есть не–P. Ни одна фиалка не является не–цветком.
2.перевод отрицания из связки в предикат: S не есть P → S есть не–P. Все мушкетеры являются
теми, кто не уклоняется от дуэлей.
Обращение – операция, при которой качество суждения остается прежним, а субъект и предикат меняются местами.
1.Все S есть P (A) → Некоторые P есть S (J). Некоторые цветы являются фиалками.
2.Ни одно S не есть P (Е) → Ни одно P не есть S (Е). Ни один человек, уклоняющийся от дуэлей, не является мушкетером.
Противопоставление предикату – логическая операция, при которой в заключении предикатом является субъект, субъектом – понятие, противоположное предикату исходного суждения, связка меняется на противоположную:
S есть P → не–P не есть S. Схема построения:

Вместо Р берем не–Р.
Меняем местами S и не–Р.
Связку меняем на противоположную.
1.Все S есть P (A) → Ни одно не–P не есть S (О) Ни один не–цветок не является фиалкой.
2.Ни одно S не есть P (Е) → Некоторые не–P есть S (J) Некоторые люди, не уклоняющиеся от дуэлей, являются мушкетерами.
Вопрос №6. Логические операции над суждениями и таблицы истинности, равносильные суждения.
Логической операцией называется образование сложных суждений из простых. В таблице 3 приведены виды логических операций В таблице 4 значения их истинности, то есть в каких случаях полученные суждения истинные, а в каких – ложные. Ложное значение обозначается 0, истинное 1.
Виды логических операций
Значение истинности логических операций
Таблица истинности – таблица, в которой показано при каких логических значениях переменных, входящих в формулу простых суждений, данное сложное суждение истинно (1), а при каких – ложно (0).
В логике говорят, что суждения равносильны, если они одновременно истинны и одновременно ложны. Одновременно, т.е. при одних и тех же значениях переменных. Обозначается равносильность
знаком . Проверку равносильности проводят с помощью таблиц истинности. Исходные суждения записывают в виде формул. Для каждой формулы составляют таблицу истинности (можно по отдельности, можно общую). Анализируют результаты: одинаковы ли полученные значения. Если да, то суждения равносильны, если есть отличия, то неравносильны.
Вопрос №7. Законы логики
Наиболее важные равносильности формул логики высказываний называют законами логики:
1.X X – закон тождества. Всякая мысль тождественная сама себе и, в процессе рассуждения, сохраняет свое значение. Необходимо следить, чтобы не было подмены значения. «Я иду в новых брюках, а ты идешь в гимназию». Два понятия «идти» – не тождественны.
2. Х |
´ |
–закон противоречия. Два противоречивых суждения об одном и том же предмете не |
X 0 |
могут быть одновременно истинны. Х – Иванов отличник, Х – Иванов не отличник (речь идет об одном и том же человеке, в один и тот же период времени).
3.Х Х 1 – закон исключенного третьего. Два противоречивых суждения об одном и том же предмете не могут быть одновременно ложными - «Завтра будет дождь или завтра не будет дождя».
4. Х |
´ |
X – закон двойного отрицания. «Неверно, что все студенты нашей группы не сдали |
зачет по логике» «Все студенты нашей группы сдали зачет по логике».
5.X Y Y Х, X Y Y Х – законы коммутативности. «Я почитаю газету или журнал» «Я
почитаю журнал или газету».
6.(X Y) Z X (Y Z); (X Y) Z X (Y Z) – законы ассоциативности. «Я схожу в
магазин, вымою пол, а также приготовлю ужин» «Я схожу в магазин, а также вымою пол и приготовлю ужин».
7.X (Y Z) (X Y) (X Z); X (Y Z) (X Y) (X Z) – законы дистрибутивности. «Я сегодня сдам зачет по геологии, а также по химии или по физике» «Я сегодня сдам зачет по геологии и по химии или по геологии и по физике».
8.X X X; X X X – закон идемпотентности. «На улице тепло, на улице тепло» «На улице тепло».
9.X 1 X; X 0 0; X 1 1; X 0 X – свойство констант.
10.Х Y Х Y; Х Y Х Y – законы де Моргана. «Неверно, что я знаю арабский или китайский язык» «Я не знаю арабского языка и не знаю китайского языка».
11.X (X Y) X; X (X Y) X – законы поглощения. «Я сдам сессию или сдам сессию и поеду домой» «Я сдам сессию».
12.X Y X Y – закон контрапозиции. «Если Винни–Пух съел мед, то он сытый» «Если Винни– Пух голоден, то он не ел мед».
13.X Y Y X ; YXYX – законы замены импликации. Если я выиграю конкурс, то получу приз» «Я не выиграю конкурс или получу приз». С помощью законов логики можно упростить суждение, выбрать более четкую формулировку.
Вопрос №8. Силлогизм: термины и посылки, фигуры и модусы. Правила силлогизмов. Ошибки посылок и вывода.
Категорический силлогизм – это умозаключение, в котором из двух простых суждений (посылок) следует новое простое суждение (заключение). Понятия в суждениях, из которых состоит силлогизм, называются терминами силлогизма. Различают больший, меньший и средний термины.
Больший термин (Р)– понятие, которое входит в одну из посылок и выступает в заключении предикатом. Посылка с этим термином называется большей и обычно ставится первой.
Меньший термин (S)– понятие, которое входит в другую посылку и выступает субъектом в заключении. Посылка с этим термином называется меньшей и обычно ставится после большей посылки.
Средний термин (М)– понятие, которое присутствует в обеих посылках и отсутствует в заключении.
Правила терминов
1.В каждом силлогизме должно быть только три термина, то есть средний термин должен быть одним и тем же в обеих посылках.
2.Средний термин должен являться или субъектом общего суждений или предикатом отрицательного суждения.

Правила посылок
Из двух частных посылок невозможно сделать заключение.
Из двух отрицательных посылок невозможно сделать заключение.
Из двух утвердительных посылок заключение всегда утвердительное.
Если есть частная посылка, то заключение всегда частное.
Если есть отрицательная посылка, то заключение всегда отрицательное.
Фигуры силлогизма – взаимное расположение терминов силлогизма друг относительно друга. Всего выделяют четыре фигуры категорического силлогизма.
Модусы:
1.I фигура:
Модус Barbara: обе посылки и вывод являются общеутвердительными суждениями;
Модус Celarent: большая посылка является общеотрицательным суждением, меньшая — общеутвердительным, а вывод — общеотрицательным;
Модус Darii: большая посылка является общеутвердительным суждением, а меньшая посылка и вывод — частноутвердительными;
Модус Ferio: большая посылка является общеотрицательным суждением, меньшая — частноутвердительным, вывод — частноотрицательным;
2.II фигура:
Модус Cesare: большая посылка является общеотрицательным суждением, меньшая посылка — общеутвердительным, а вывод — общеотрицательным;
Модус Camestres: большая посылка является общеутвердительным суждением, меньшая посылка и вывод являются общеотрицательными суждениями;
Модус Festino: большая посылка является общеотрицательным суждением, меньшая посылка — общеутвердительным, а вывод — частноотрицательным. Иными словами, вывод является обращением вывода модуса Ferio;
Модус Baroko: большая посылка является общеутвердительным суждением, меньшая
посылка и вывод — частноотрицательными.
Правила второй фигуры:
одна из посылок является отрицательным суждением,
вывод является отрицательным суждением,
большая посылка является общим суждением
3.III фигура:
Модус Darapti: большая и меньшая посылки являются общеутвердительными суждениями; вывод является частноутвердительным суждением.
Модус Disamis: большая посылка и вывод — частноутвердительные суждения, меньшая посылка — общеутвердительное суждение.
Модус Datisi: большая посылка является общеутвердительным суждением, меньшая посылка и вывод – частноутвердительными.
Модус Felapton: большая посылка является общеотрицательным суждением, меньшая посылка — общеутвердительным, вывод — частноотрицательное суждение.
Модус Bokardo: большая посылка и вывод — частноотрицательные суждения, меньшая посылка - общеутвердительное суждение.
Модус Ferison: большая посылка — общеотрицательное суждение, меньшая посылка —
частноутвердительное суждение, вывод — частноотрицательное суждение.
Правила третьей фигуры:
меньшая посылка является утвердительным суждением;
вывод является частным суждением.
4.IV фигура:
Модус Bramantip: большая и меньшая посылки являются общеутвердительными суждениями, а вывод — частноутвердительным, при этом средний термин — субъект меньшей и предикат большей посылок.
Модус Camenes: большая посылка — общеутвердительное суждение, меньшая посылка и вывод — общеотрицательные.
Модус Dimaris: Большая посылка и вывод — частноутвердительные суждения, меньшая посылка — общеутвердительное суждение.
Модус Fesapo: большая посылка — общеотрицательное суждение, меньшая — общеутвердительное суждение, вывод — частноотрицательное суждение.
Модус Fresison: большая посылка — общеотрицательное суждение, меньшая посылка —
частноутвердительное суждение, вывод — частноотрицательное суждение.
Правила четвертой фигуры:
если большая посылка является утвердительным суждением, то меньшая посылка является общим суждением;
если меньшая посылка является утвердительным суждением, то вывод является частным суждением,
в отрицательных модусах большая посылка является общим суждением.
Вопрос №9. Диаграмма Эйлера-Венна.
Любое высказывание на диаграмме изображается кругом, а его отрицание - частью плоскости, находящейся вне круга.
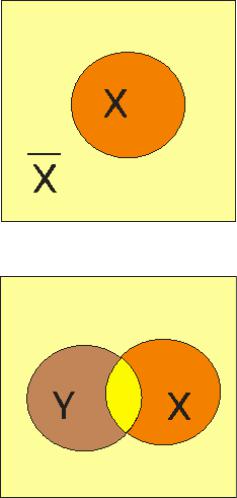
Рисунок. Диаграмма Эйлера -Венна
Если у нас есть два высказывания X и Y, то их на диаграмме изображают двумя кругами, как правило, разного цвета.
Рисунок. Логическое умножение двух высказываний X и Y
Вопрос №11. Методы доказательства: прямой, обратный и «от противного».
При доказательстве теорем применяется логическая аргументация. Доказательства в информатике неотъемлемая часть проверки корректности алгоритмов. Необходимость доказательства возникает, когда нам нужно установить истинность высказывания вида (А В). Существует несколько стандартных типов доказательств, включающих следующие:
1.Прямое рассуждение (доказательство). Предполагаем, что высказывание А истинно и показываем справедливость В. Такой способ доказательства исключает ситуацию, когда A истинно, a B ложно, поскольку именно в этом и только в этом случае импликация (А В) принимает ложное значение (см. табл). Таким образом, прямое доказательство идет от рассмотрения аргументов к доказательству тезиса, т. е. истинность тезиса непосредственно обосновывается аргументами. Схема этого доказательства такая: из данных аргументов (а, b, с, ...) необходимо следует доказываемый тезис q.
2.Обратное рассуждение (доказательство). Предполагаем, что высказывание В ложно и показываем ошибочность А. То есть, фактически, прямым способом проверяем истинность импликации ((не В) (не А)), что согласно таблицы, логически эквивалентно истинности исходного утверждения (А В).
3.Метод «от противного». Этот метод часто используется в математике. Пусть а - тезис или теорема, которую надо доказать. Предполагаем от противного, что а ложно, т. е. истинно не-а (или ). Из допущения выводим следствия, которые противоречат действительности или ранее доказанным теоремам. Имеем , при этом - ложно, значит, истинно его отрицание, т.е. , которое по закону двузначной классической логики (→а) дает а. Значит, истинно а, что и требовалось доказать. Примеров доказательства “от противного” очень много в школьном курсе математики. Так, пример, доказывается теорема о том, что из точки, лежащей вне прямой, на эту прямую можно опустить лишь один перпендикуляр. Методом “от противного” доказывается и следующая теорема: “Если
две прямые перпендикулярны к одной и той же плоскости, то они параллельны”. Доказательство этой теоремы пpямо начинается словами: “Предположим противное, т. е. что прямые АВ и CD не параллельны”.
Вопрос №12. Принцип математической индукции.
Принцип математической индукции это следующая теорема: Пусть мы имеем бесконечную последовательность утверждений P1,P2,...,Pn занумерованных натуральными числами, причём: утверждение P1 истинно; если некоторое утверждение Pk истинно, то следующее утверждение Pk+1 тоже истинно. Тогда принцип математической индукции утверждает, что все утверждения последовательности истинны. Другими словами принцип математической индукции можно сформулировать так: если в очереди первой стоит женщина, и за каждой женщиной стоит женщина, то все в очереди – женщины. Способ рассуждений, основанный на принципе математической индукции называется методом математической индукции. Для решения задач методом математической индукции необходимо:
1. сформулировать утверждение задачи в виде последовательности утверждений P1, P2, ..., Pn , ... ; 2. доказать, что утверждение P1 истинно (этот этап называется базой индукции);
3.доказать, что если утверждение Pn истинно при некотором n= k, то оно истинно и при n = k + 1 (этот этап называется шагом индукции). Ввиду недостоверности заключения индукция не может служить методом доказательства. Но она является мощным эвристическим методом, т. е. методом открытия новых истин.
