
III. Квантовая оптика
1. Тепловое излучение
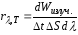 –спектральная
плотность энергетической светимости;
–спектральная
плотность энергетической светимости;
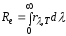 –энергетическая
светимость;
–энергетическая
светимость;
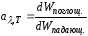 –спектральная
поглощательная способность, для абсолютно
черного тела
–спектральная
поглощательная способность, для абсолютно
черного тела
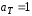 ;
;
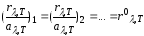 –закон Кирхгофа,
где
–закон Кирхгофа,
где
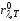 – универсальная функция Кирхгофа
одинаковая для всех черных тел;
– универсальная функция Кирхгофа
одинаковая для всех черных тел;
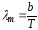 –закон смещения
Вина, где b=2,90.10-3
м.К;
–закон смещения
Вина, где b=2,90.10-3
м.К;
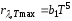 –закон Вина, где
b1=1,29.10-5
Вт.м-3.К-5;
–закон Вина, где
b1=1,29.10-5
Вт.м-3.К-5;
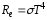 –закон
Стефана-Больцмана,
–закон
Стефана-Больцмана,
где
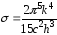 =5,67.10-8
Вт.м-2К-4;
=5,67.10-8
Вт.м-2К-4;
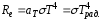 –для серого тела,
где аТ
– коэффициент серости (черноты);
–для серого тела,
где аТ
– коэффициент серости (черноты);
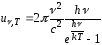 –формула Планка.
–формула Планка.
2. Квантовые свойства света
а) Энергия, импульс фотона. Давление света
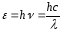 –энергия
фотона;
–энергия
фотона;
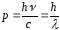 –импульс фотона;
–импульс фотона;
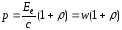 –давление света;
–давление света;
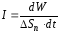 –интенсивность
света.
–интенсивность
света.
б) Внешний фотоэлектрический эффект
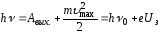 –уравнение
Эйнштейна для внешнего фотоэффекта;
–уравнение
Эйнштейна для внешнего фотоэффекта;
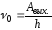 ;
;
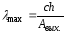 – красная граница фотоэффекта;
– красная граница фотоэффекта;
в) Эффект Комптона
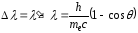 –изменение длины
волны при эффекте Комптона.
–изменение длины
волны при эффекте Комптона.
Примеры решения задач
Задача 1
Теплопроводящий шар по размеру равен объему Земли (R=6.4.106 м). Удельная теплоемкость 200 Дж/кг.К, плотность шара 5500 кг/м3, начальная температура 300 К. Определить время остывания шара на 0,001 К. Шар считать абсолютно черным.
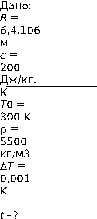 Решение:
Решение:
По определению
полной энергетической светимости:
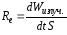 ;
здесь
;
здесь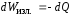 – энергия, излучённая телом площадиS
за время dt;
– энергия, излучённая телом площадиS
за время dt;
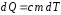 – количество теплоты, полученной телом
массойm
при нагреве на dT.
По закону Стефана-Больцмана для абсолютно
чёрного тела
– количество теплоты, полученной телом
массойm
при нагреве на dT.
По закону Стефана-Больцмана для абсолютно
чёрного тела
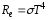 .
Тогда
.
Тогда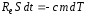 ,
или
,
или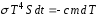 ,
откуда
,
откуда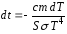 .
Проинтегрируем это равенство и вынесем
постоянные величины за знак интеграла:
.
Проинтегрируем это равенство и вынесем
постоянные величины за знак интеграла: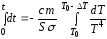 .
Отсюда
.
Отсюда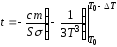 ,
,
или:
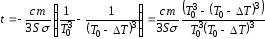 .
После преобразований получим:
.
После преобразований получим: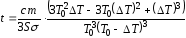 .
Поскольку
.
Поскольку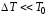 ,
в числителе можно пренебречь двумя
последними слагаемыми, и в знаменателе
– вторым слагаемым; тогда
,
в числителе можно пренебречь двумя
последними слагаемыми, и в знаменателе
– вторым слагаемым; тогда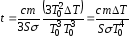 .
.
Масса шара
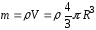 ,
а площадь поверхности
,
а площадь поверхности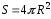 ,
тогда
,
тогда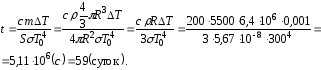
Задача 2
Монохроматический пучок света интенсивностью 0,1 Вт/см2 падает под углом 30о на плоскую отражающую поверхность с коэффициентом отражения 0,7. Определить нормальное давление, оказываемое светом на эту поверхность.
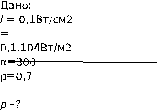
 Решение:
Решение:
Пусть на поверхность
площадью S
за время Δt
падает N
фотонов. По условию ρ=0.7, то есть 70% фотонов
отражается (N1=ρN=0.7N),
30% – поглощается (N2=(1–ρ)N=0.3N).
Импульс фотона равен
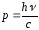 .
При отражении изменение импульса фотона
.
При отражении изменение импульса фотона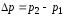 направлено по нормали к площадке и равно
по величине
направлено по нормали к площадке и равно
по величине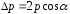 (см. рис.1), здесь
(см. рис.1), здесь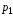 –
импульс падающего фотона,
–
импульс падающего фотона,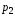 – импульс отражённого фотона.
– импульс отражённого фотона.
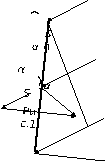 Изменение
величины импульса поглощённого фотона
равно величине самого импульса; его
проекция на нормаль к площадке (поскольку
требуется найти нормальное
давление):
Изменение
величины импульса поглощённого фотона
равно величине самого импульса; его
проекция на нормаль к площадке (поскольку
требуется найти нормальное
давление):
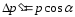 .
По закону сохранения импульса суммарное
изменение импульса фотонов равно
величине импульса, полученного площадкой:
.
По закону сохранения импульса суммарное
изменение импульса фотонов равно
величине импульса, полученного площадкой: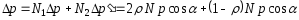 ,
или
,
или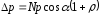 ,
откуда по второму закону Ньютона в
импульсной форме
,
откуда по второму закону Ньютона в
импульсной форме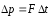 найдём силу нормального давления света:
найдём силу нормального давления света: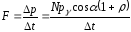 ,
и давление:
,
и давление: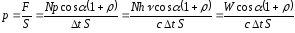 ,
,
где W
– суммарная энергия всех фотонов,
падающих на площадку S
за время
Δt.
Выразим W
через интенсивность света I:
интенсивностью света называется энергия
световой волны, переносимая за единицу
времени через единичную площадку,
перпендикулярную лучу:
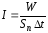 ;
здесь
;
здесь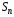 – величина площадки, перпендикулярной
лучу, так что
– величина площадки, перпендикулярной
лучу, так что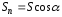 (см. рис.),
(см. рис.), .
Тогда
.
Тогда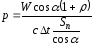 ,
или
,
или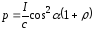 .
.
Подставим
численные значения:
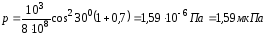 .
.
Задача 3
Угол рассеяния фотона при эффекте Комптона 90o. Угол отдачи электрона 30o. Определить энергию падающего фотона.
 Решение:
Решение:
 По
закону сохранения импульса: импульс
падающего фотона равен сумме импульса
электрона отдачи и импульса рассеянного
фотона:
По
закону сохранения импульса: импульс
падающего фотона равен сумме импульса
электрона отдачи и импульса рассеянного
фотона:
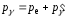
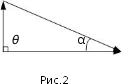
(см. рис.2). Из рисунка
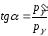 .
Импульс фотона выразим через длину
волныλ
падающего фотона и рассеянного
.
Импульс фотона выразим через длину
волныλ
падающего фотона и рассеянного
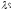 :
: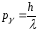 ,
,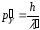 ,
тогда
,
тогда ,
или
,
или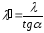 .
Длины волн падающего и рассеянного
фотона связаны соотношением:
.
Длины волн падающего и рассеянного
фотона связаны соотношением: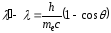 .
Подставим в него выражение для
.
Подставим в него выражение для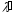 :
: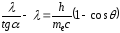 .
.
Отсюда можно выразить λ:
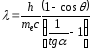 .
.
Энергия
фотона
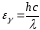 ,
следовательно,
,
следовательно,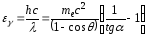
Подставим численные значения:
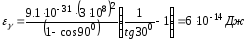 .
.
