3.4. Проверка устойчивости системы по критерию Михайлова

Подставим в этот полином вместо p мнимую переменную j. В результате получим комплексную функцию

Здесь U_D() - действительная часть, полученная из членов А(р), содержащих четные члены р, a V_D() - мнимая часть, полученная из членов А(р) с нечетными степенями р.

Изобразим A(j) в виде годографа в комплексной плоскости. Этот годограф называется годографом Михайлова.

Критерий Михайлова формулируется так: система устойчива, если годограф A(j), начинаясь на действительной положительной полуоси, огибает против часовой стрелки начало координат, проходя последовательно n квадрантов, где n - порядок системы.

Для проверки устойчивости по критерию Михайлова заменим в характеристическом уравнение р на j.

A(j) = 0,00288 * (j)⁴ + 0,1654 * (j)³ + 0,318 * (j)² + j + 0,18 =

= 0,00288 * ⁴ - 0,1654 * j³ - 0,318 * ² + j + 0,18 =

= 0,00288 * ⁴ - 0,318 * ² + j (- 0,1654³) + 0,18

Найдем точки пересечения годографа вектора частотной функции F(j) с осями на комплексной плоскости:

a) с j

0,00288 * ⁴ - 0,318 * ² + 0,18 = 0

₁ = 10,48;

₂ = 0,75;

при ₁ j₁= ₁- 0,1654₁³ = 10,48 - 0,1654*10,48³ = -179,9

при ₂ j₂= ₂- 0,1654₂³ = 0,75 - 0,1654*0,75³ = 0,7

б) с “+1;-1”

- 0,1654³= 0

₃= 0;

₄= 2,46;

при ₃ “+1” = 0,00288 * ₃⁴ - 0,318 * ₃² + 0,18 = 0,18

при ₄ “-1” = 0,00288 * ₄⁴ - 0,318 * ₄² + 0,18 = -1,64

Годограф последовательно проходит четыре квадранта. Годограф берет свое начало из точки 0,18, находящейся на действительной положительной полуоси и проходит последовательно против часовой стрелки 4 квадранта. Следовательно, по критерию Михайлова система устойчива.

3.5. Определение статической и скоростной ошибки

1. Поскольку исследуемая САР в структуре имеет астатическое звено, то статическая ошибка САР равна 0.

2. Коэффициент ошибки по скорости:

1/k1k2k3 = l / (0.12*0.15* 10) = 5,56

4. Оценка показателей точности работы сар

4.1. Частотные критерии качества переходных процессов

Для минимально-фазовых систем качество переходных процессов может быть оценено по амплитудной характеристике замкнутой системы Аз().

Построим АЧХ для передаточной функции:

Для этого заменим коэффициент р на j. тогда получим

Отделим мнимую часть от действительной.

отделим амплитуду от фазы

Построим АЧХ

По АЧХ можно оценить колебательность и длительность переходной характеристики системы. Колебательность определяется по величине относи-тельного максимума характеристики, который поэтому называется показателем колебательности:

М=А(p)/А(0)

М=0,32/0,045=7,11

Длительность переходной характеристики может быть оценена по величине резонансной частоты _p.

t_max =  / _p

t_max = l.4c

4.2. Корневые критерии качества переходных процессов

Чтобы проверить корневые критерии качества, необходимо решить следующее уравнение четвертой степени

0,00288 ⁴ + 0,1654 ³ + 0,318 ² +  + 0,18 = 0

Найдем корни этого уравнения:

 ₁ = -31.6584

 ₂ = -0,8645 – 2,4659 j

 ₃ = -0,8645 + 2,4659 j

 ₄ = -0,5456

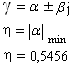
Чтобы корневые критерии качества выполнялись, должно выполнять-ся соотношение:

следовательно, корневые критерии качества выполняются.