Karmazin_-_Teoria_Igr_Uchebnik / P8_3
.DOCТема 8. РЕШЕНИЕ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ С ПАРАМЕТРОМ В СВОБОДНЫХ ЧЛЕНАХ СИСТЕМЫ ОГРАНИЧЕНИЙ
Пусть требуется
для каждого значения параметра
решить следующую задачу линейного
программирования (ЛП):
, (1)
, (2)
. (3)
Эту задачу ещё называют задачей ЛП с параметром в правой части ограничений-равенств, или задачей ЛП с параметром в правой части.
Решением задачи
ЛП (1)
(3) назовем такое разбиение вещественной
прямой на конечное число промежутков
(их объединение совпадает с
),
для каждого из которых либо указан
вектор
,
являющийся оптимальным решением задачи
ЛП при всех значениях
из данного промежутка, либо при всех
из данного промежутка задача (1)
(3) не имеет решения.
Изучим поведение
решения задачи (1)
(3) в зависимости от изменения параметра
.
Допустим, что найдено оптимальное
решение
задачи при
.
Каждая его компонента
линейная функция от
,
т.е.
и система неравенств
(4)
является совместной.
Если все
,
то решение
является оптимальным для всех
.
Если все
,
то решение
оптимально для всех
.
Наконец, если все
,
то решение
оптимально для всех
.
В общем случае
могут быть как положительными, так и
отрицательными. Поэтому при определении
интервала значений
,
на котором данное решение оптимально,
необходимо провести исследование
системы неравенств (4).
Для
имеем
.
Положим
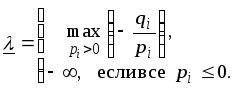
Если
,
то
.
Положим
Очевидно, что
решение
оптимально для всех
из интервала
.
Допустим, что
.
При увеличении
вектор
с компонентами
по-прежнему удовлетворяет условию
оптимальности, т.е.
.
Однако этот вектор
может и не являться решением рассматриваемой
задачи. При достаточно большом увеличении
одна из величин
становится отрицательной.
Пусть при увеличении
компонента
первая стала отрицательной, тогда
.
Теперь необходимо определить, существует
ли новое оптимальное решение при
.
Для этого надо выбрать такой вектор,
подлежащий введению в базис, и такой
вектор, исключаемый из базиса, чтобы
компоненты нового решения и соответствующие
ему оценки
были
неотрицательными. Выбор исключаемого
из базиса и вводимого в базис векторов
осуществляется по тем же правилам, что
и в двойственном симплекс-методе.
Теорема 1.
Если вектор
,
соответствующий
,
исключается из базиса и в базис включается
вектор
,
для которого
то образуется
новое оптимальное решение хотя бы для
одного значения
.
Если новый базис определяет решение
задачи для интервала
,
то
.
Если все
,
то исследуемая задача при
не имеет ни одного решения.
Алгоритм решения задачи линейного программирования с параметром в свободных членах системы ограничений сводится к следующему:
а) используя
симплекс-метод, находим такой базис,
для которого система неравенств
совместна и оценки векторов
;
б) определяем
и
;
в) исследуем задачу
как для
,
так и для
,
и переходим от одного интервала изменения
к другому до тех пор, пока не рассмотрим
все множество
.
Пример 1. Решить
задачу ЛП с параметром
в свободных членах системы ограничений
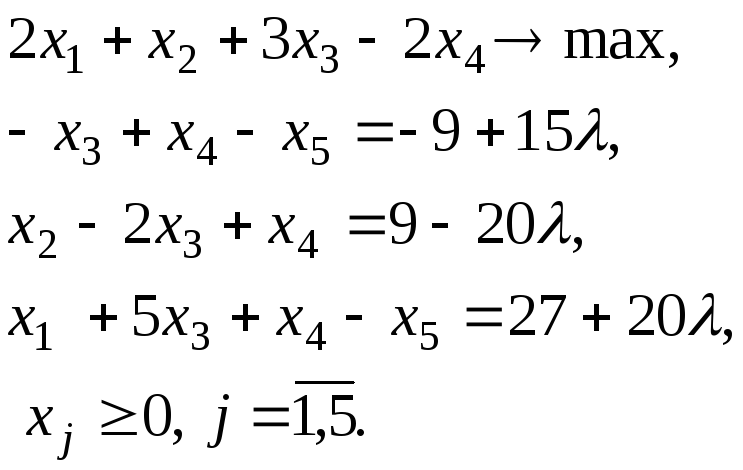
Преобразуем систему
ограничений так, чтобы при
задача ЛП имела канонический вид, и
затем решим её M-методом.
В табл. 1 вектор
столбец правой части ограничений
представляем двумя векторами
и
.
Таблица 1
|
|
№ |
Базис |
Сбаз |
A |
0 |
2 |
1 |
3 |
-2 |
0 |
-M |
|
|
|
|
|
|
|
A1 |
A2 |
A3 |
A4 |
A5 |
A6 |
|
|
1 |
A6 |
-M |
9 |
-15 |
0 |
0 |
1 |
-1 |
"1" |
1 |
|
|
2 |
A2 |
1 |
9 |
-20 |
0 |
1 |
-2 |
1 |
0 |
0 |
|
|
3 |
A1 |
2 |
27 |
20 |
1 |
0 |
5 |
1 |
-1 |
0 |
|
|
4 |
- |
- |
- |
- |
0 |
0 |
4 |
5 |
-2 |
0 |
|
|
5 |
- |
- |
- |
- |
0 |
0 |
-1 |
1 |
-1 |
0 |
В табл. 2
(элементы 4-й строки таблицы), и не зависят
от
.
Таким образом, если компоненты вектора
неотрицательны, то он является оптимальным
опорным решением; для этого параметр
должен удовлетворять системе неравенств
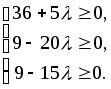
Таблица
2
|
|
№ |
Базис |
Сбаз |
A |
0 |
2 |
1 |
3 |
-2 |
0 |
|
|
|
|
|
|
|
A1 |
A2 |
A3 |
A4 |
A5 |
|
|
1 |
A5 |
0 |
9 |
-15 |
0 |
0 |
1 |
-1 |
1 |
|
|
2 |
A2 |
1 |
9 |
-20 |
0 |
1 |
"-2" |
1 |
0 |
|
|
3 |
A1 |
2 |
36 |
5 |
1 |
0 |
6 |
0 |
0 |
|
|
4 |
- |
- |
81 |
-10 |
0 |
0 |
7 |
3 |
0 |
Отсюда получаем
и
.
Исследуем задачу
ЛП при
.
В этом случае 1-я компонента вектора
станет отрицательной, и чтобы перейти
к опорному решению, надо, согласно
двойственному симплекс-методу, вывести
из базиса вектор
.
Как видно из табл. 2 все элементы 3-й
строки неотрицательны (
),
и, следовательно, при
наша задача ЛП не имеет решений.
Исследуем задачу
ЛП при
.
В этом случае 2-я компонента вектора
станет отрицательной, и чтобы перейти
к опорному решению, выводим из базиса
вектор
и вводим в базис вектор
(табл. 2).
В результате такого преобразования
получим табл. 3.
Таблица
3
|
|
№ |
Базис |
Сбаз |
A |
0 |
2 |
1 |
3 |
-2 |
0 |
|
|
|
|
|
|
|
A1 |
A2 |
A3 |
A4 |
A5 |
|
|
1 |
A5 |
0 |
27/2 |
-25 |
0 |
1/2 |
0 |
"-1/2" |
1 |
|
|
2 |
A3 |
3 |
-9/2 |
10 |
0 |
-1/2 |
1 |
-1/2 |
0 |
|
|
3 |
A1 |
2 |
63 |
-55 |
1 |
3 |
0 |
3 |
0 |
|
|
4 |
- |
- |
225/2 |
-80 |
0 |
7/2 |
0 |
11/2 |
0 |
Из табл. 3 следует,
что вектор
является оптимальным опорным решением
задачи при
.
Рассмотрим случай
,
в котором отрицательной становится 5-я
компонента вектора. Выводим из базиса
вектор
и вводим вектор
,
результат этих действий приведен в
табл. 4. Из этой таблицы видно, что
.
Таким образом мы исследовали решения
задачи ЛП при всех значениях параметра
.
Таблица 4
|
|
№ |
Базис |
Сбаз |
A |
0 |
2 |
1 |
3 |
-2 |
0 |
|
|
|
|
|
|
|
A1 |
A2 |
A3 |
A4 |
A5 |
|
|
1 |
A4 |
-2 |
-27 |
50 |
0 |
-1 |
0 |
1 |
-2 |
|
|
2 |
A3 |
3 |
-18 |
35 |
0 |
-1 |
1 |
0 |
-1 |
|
|
3 |
A1 |
2 |
144 |
95 |
1 |
6 |
0 |
0 |
6 |
|
|
4 |
- |
- |
288 |
195 |
0 |
10 |
0 |
0 |
13 |
Сформулируем итоги решения задачи:
1) задача не имеет
решений при
;
2)
при
;
3)
,
при
;
4)
при
.
Задание.
Решить каноническую задачу линейного
программирования (1)
(3) с параметром в правой части равенств
ограничений для значений
,
,
и
,
заданных в 8.1
8.105.
|
8.1 A= ; B'= ; B'' = ;
|
|
8.2 A= ; B'= ; B'' = ;
|
|
8.3 A= ; B'= ; B'' = ;
|
|
8.4 A= ; B'= ; B'' = ;
|
|
8.5 A= ; B'= ; B'' = ; |
|
8.6 A= ; B'= ; B'' = ;
|
|
8.7 A= ; B'= ; B'' = ;
|
|
8.8 A= ; B'= ; B'' = ;
|
|
8.9 A= ; B'= ; B'' = ;
|
|
8.10 A= ; B'= ; B'' = ;
|
|
8.11 A= ; B'= ; B'' = ;
|
|
8.12 A= ; B'= ; B'' = ;
|
|
8.13 A= ; B'= ; B'' = ;
|
|
8.14 A= ; B'= ; B'' = ;
|
|
8.15 A= ; B'= ; B'' = ;
|
|
8.16 A= ; B'= ; B'' = ;
|
|
8.17 A= ; B'= ; B'' = ;
|
|
8.18 A= ; B'= ; B'' = ;
|
|
8.19 A= ; B'= ; B'' = ;
|
|
8.20 A= ; B'= ; B'' = ;
|
|
8.21 A= ; B'= ; B'' = ;
|
|
8.22 A= ; B'= ; B'' = ;
|
|
8.23 A= ; B'= ; B'' = ;
|
|
8.24 A= ; B'= ; B'' = ;
|
|
8.25 A= ; B'= ; B'' = ;
|
|
8.26 A= ; B'= ; B'' = ;
|
|
8.27 A= ; B'= ; B'' = ;
|
|
8.28 A= ; B'= ; B'' = ;
|
|
8.29 A= ; B'= ; B'' = ;
|
|
8.30 A= ; B'= ; B'' = ;
|
|
8.31 A= ; B'= ; B'' = ;
|
|
8.32 A= ; B'= ; B'' = ;
|
|
8.33 A= ; B'= ; B'' = ;
|
|
8.34 A= ; B'= ; B'' = ;
|
|
8.35 A= ; B'= ; B'' = ;
|
|
8.36 A= ; B'= ; B'' = ;
|
|
8.37 A= ; B'= ; B'' = ;
|
|
8.38 A= ; B'= ; B'' = ;
|
|
8.39 A= ; B'= ; B'' = ;
|
|
8.40 A= ; B'= ; B'' = ;
|
|
8.41 A= ; B'= ; B'' = ;
|
|
8.42 A= ; B'= ; B'' = ;
|
|
8.43 A= ; B'= ; B'' = ;
|
|
8.44 A= ; B'= ; B'' = ;
|
|
8.45 A= ; B'= ; B'' = ;
|
|
8.46 A= ; B'= ; B'' = ;
|
|
8.47 A= ; B'= ; B'' = ;
|
|
8.48 A= ; B'= ; B'' = ;
|
|
8.49 A= ; B'= ; B'' = ;
|
|
8.50 A= ; B'= ; B'' = ;
|
|
8.51 A= ; B'= ; B'' = ;
|
|
8.52 A= ; B'= ; B'' = ;
|
|
8.53 A= ; B'= ; B'' = ;
|
|
8.54 A= ; B'= ; B'' = ;
|
|
8.55 A= ; B'= ; B'' = ;
|
|
8.56 A= ; B'= ; B'' = ;
|
|
8.57 A= ; B'= ; B'' = ;
|
|
8.58 A= ; B'= ; B'' = ;
|
|
8.59 A= ; B'= ; B'' = ;
|
|
8.60 A= ; B'= ; B'' = ;
|
|
8.61 A= ; B'= ; B'' = ;
|
|
8.62 A= ; B'= ; B'' = ;
|
|
8.63 A= ; B'= ; B'' = ;
|
|
8.64 A= ; B'= ; B'' = ;
|
|
8.65 A= ; B'= ; B'' = ;
|