Karmazin_-_Teoria_Igr_Uchebnik / P7_3

Тема 7. РЕШЕНИЕ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ С ПАРАМЕТРОМ В ЦЕЛЕВОЙ ФУНКЦИИ

Основная трудность, возникающая при практическом использовании линейного программирования (ЛП), состоит в определении достаточно точных и надежных числовых параметров задачи. Исследование поведения решения задачи ЛП при изменении её коэффициентов составляют предмет параметрического ЛП.

Пусть требуется для каждого значения параметра решить следующую задачу ЛП:

, (1)

, (2)

. (3)

Такая задача называется канонической задачей ЛП с параметром в целевой функции.

Решением параметрической задачи ЛП (1)  (3) назовем такое разбиение вещественной прямой на конечное число промежутков (их объединение совпадает с ), для каждого из которых либо указан вектор , являющийся оптимальным решением задачи ЛП при всех значениях из данного промежутка, либо при всех из этого промежутка задача (1)  (3) не имеет решения.

Изучим поведение решения задачи (1)  (3) в зависимости от изменения параметра . Положим = и решим задачу ЛП симплекс-методом. Возможны два случая:

1) при данном найден (существует) оптимальный план;

2) при данном целевая функция (1) не ограничена сверху на допустимом множестве.

Рассмотрим каждый из случаев.

1. Вычислив, по формуле (6) из темы 2, оценки векторов относительно оптимального базиса , получим

, (4)

где

, (5)

. (6)

Обозначим

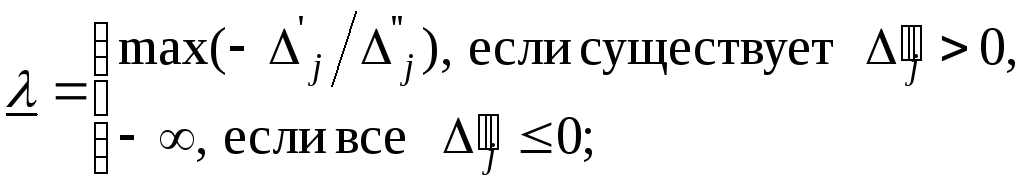(7)

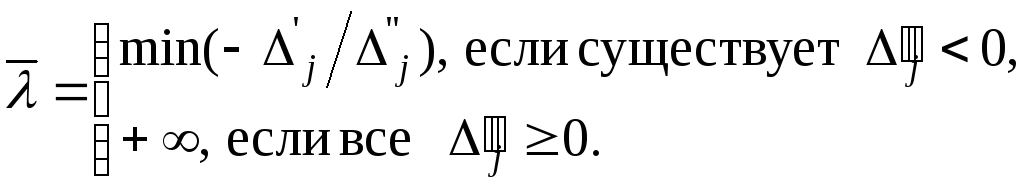(8)

Полная совокупность значений параметра , при котором рассматриваемый базис оптимален, называется множеством оптимальности этого базиса.

Тогда множество оптимальности базиса состоит из всех значений .

Исследуем задачу (1)  (3) для . Будем предполагать, что , а это означает на основании (8), что среди имеются отрицательные.

Пусть

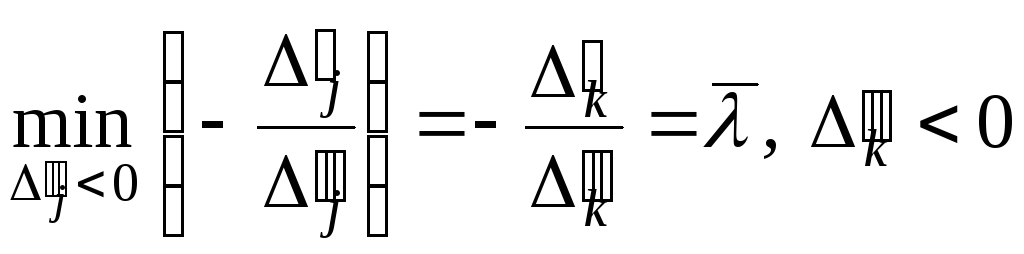. (9)

Теорема 1. Пусть и индекс k определяется условием (9) , тогда: а) если все , то линейная форма (1) не ограничена на множестве (2), (3) для всех ; б) если некоторое , то, введя в имеющийся базис вектор по обычным правилам симплекс-метода, приходим к новому базису, левый конец множества оптимальности которого совпадает с .

Таким образом, процесс исследования параметрической задачи для сводится к движению по базисам её соседних планов, причем правая граница множества оптимальности предыдущего базиса является левой границей для множества оптимальности последующего базиса. Процесс обрывается построением луча, являющегося либо множеством оптимальности последнего базиса, либо множеством, в каждой точке которого задача неразрешима.

Приведенные нами построения могут быть повторены для . Для этого необходимо заменить правило выбора (9) на следующее:

. (10)

2. Рассмотрим второй случай, когда для процесс построения базиса задачи (1)  (3) оканчивается условием неразрешимости:

, (11)

где  вектор, не входящий в базис.

Если , то соотношение (11) выполняется при любом и задача (1)  (3) неразрешима на всей оси . Если , то условие (11) соблюдается для всех . Если , то условие (11) выполняется для всех . Следовательно, при задача (1)  (3) неразрешима справа от , для  слева от .

Очевидно, для дальнейшего анализа задачи ( ) необходимо в качестве взять и провести решение. Если получим оптимальный план, то дальнейший анализ проводится по случаю один. Если получим , то вновь переходим к анализу задачи, в качестве выбирая . Если получим , то приходим к выводу, что задача (1)  (3) неразрешима справа от , т.е. при , но , а ранее было получено, что задача (1)  (3) неразрешима справа от . Значит она неразрешима всюду. Такой же вывод получаем, если .

Подводя итог, отметим: решение задачи ЛП с параметром в целевой функции производится по симплекс-методу, но вместо одной строки оценок вводятся три строки для случая 1; две строки для случая 2.

Процесс анализа задачи сводится к следующему.

Решаем задачу при . Возможны случаи 1 или 2. В случае 1 вводим три строки оценок, причем в строке выполняются позиции, отвечающие . Если все позиции последней строки оказались незаполненными, то текущий базис оптимален для . В противном случае индекс минимального элемента этой строки определяет номер вектора, подлежащего включению в базис, а значение минимального элемента совпадает с правой границей множества оптимальности текущего базиса.

В случае 2 при фиксируем неразрешимость задачи для всех , а при заполняем строку .

Пример 1. Решить каноническую задачу ЛП с параметром в целевой функции, где:

.

Положим, например, и решим соответствующую задачу ЛП М-методом ( табл. 1  3 ) .

Из табл. 3 следует, что получен оптимальный базис, так как . Перейдем теперь непосредственно к решению параметрической задачи ЛП. Для этого в табл.3 добавим строку (4-ю строку), при этом находятся в 3-й строке. В пятую строку поместим отношения , отвечающие .

Таблица 1  3

	№	Базис	Сбаз	A0	-1	-1	-1	-1	-M	-M
					A1	A2	A3	A4	A5	A6
	1	A5	-M	2	1	3	-1	-1	1	0
¬	2	A6	-M	3	"2"	-1	1	-1	0	1
	3	-	-	0	1	1	1	1	0	0
	4	-	-	-5	-3	-2	0	2	0	0
						¯
¬	1	A5	-M	1/2	0	"7/2"	-3/2	-1/2	1	-1/2
	2	A1	-1	3/2	1	-1/2	1/2	-1/2	0	1/2
	3	-	-	-3/2	0	3/2	1/2	3/2	0	-1/2
	4	-	-	-1/2	0	-7/2	3/2	1/2	0	3/2
	1	A2	-1	1/7	0	1	-3/7	-1/7
	2	A1	-1	11/7	1	0	2/7	-4/7
	3	-	-	-12/7	0	0	8/7	12/7

Используя формулы (7) и (8) находим, что , . Таким образом, множество оптимальности базиса есть отрезок . При этом , .

Исследуем теперь задачу для . Имеем . При этом . Следовательно, это означает, что задача неразрешима при , т.е. при .

Таблица 4

	№	Базис	Сбаз		A0	-1	-1	-1	-1
						0	1	-2	0
						A1	A2	A3	A4
	1	A2	-1	1	1/7	0	1	-3/7	-1/7
¬	2	A1	-1	0	11/7	1	0	"2/7"	-4/7
	3	-	-		-12/7	0	0	8/7	12/7
	4	-	-		1/7	0	0	11/7	-1/7
						-	-	-	12

Исследуем теперь задачу при . Имеем . При этом, только . Это означает, что в базис необходимо ввести вектор , а вывести второй по счету вектор базиса, т.е. .

Таким образом, получаем табл. 5.

Таблица 5

	№	Базис	Сбаз		A0	-1	-1	-1	-1
						0	1	-2	0
						A1	A2	A3	A4
	1	A2	-1	1	5/2	3/2	1	0	-1
	2	A3	-1	-2	11/2	7/2	0	1	-2
	3	-	-		-8	-4	0	0	4
	4	-	-		-17/2	-11/2	0	0	3
						-8/11	-	-	-

Следовательно, . Тогда отрезок представляет собой множество оптимальности базиса . При этом , при .

Исследуем теперь задачу при . Имеем . При этом . Следовательно, можно утверждать, что задача неразрешима при , т.е. при .

Итак, параметрическая задача ЛП решена полностью, так как исчерпаны все значения параметра . Итоги решения задачи можно записать в виде:

при ;

, при ;

, при ;

при .

Отметим также, что из приведенных результатов следует, что параметрическая задача ЛП при имеет бесконечно много решений, а именно, отрезок , т.е. множество векторов вида , где .

Задание. Решить каноническую задачу линейного программирования (1)  (3) с параметром в целевой функции для значений коэффициентов