
Karmazin_-_Teoria_Igr_Uchebnik / P3_3
.DOCТема 3. РЕШЕНИЕ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ СИМПЛЕКС-МЕТОДОМ
С ИСПОЛЬЗОВАНИЕМ ИСКУССТВЕННОГО БАЗИСА
Для начала работы симплекс-алгоритма необходимо знать некоторое опорное решение задачи. Поэтому обычно каноническую задачу (1) (3) из темы 2, введением искусственного базиса сводят к решению вспомогательной задачи линейного программирования с очевидным опорным решением, причем с единичным базисом.
Предположим, что задача записана в виде:
![]()
![]() (1)
(1)
![]()
![]()
где
![]() .
Здесь выделены переменные
.
Здесь выделены переменные
![]() с различными единичными векторами
с различными единичными векторами
![]() ( таких переменных может и не быть,
тогда
( таких переменных может и не быть,
тогда
![]() ).
).
Рассмотрим вспомогательную задачу:
![]()
![]() (2)
(2)
![]()
![]()
Здесь
![]()
некоторое достаточно большое положительное
число. Переменные
некоторое достаточно большое положительное
число. Переменные
![]() называются искусственными
переменными,
а соответствующие им единичные векторы
называются искусственными
переменными,
а соответствующие им единичные векторы
![]()
искусственными
векторами.
Задачу (2) будем называть M-задачей.
Легко видеть,
что задача (2) имеет опорное решение
искусственными
векторами.
Задачу (2) будем называть M-задачей.
Легко видеть,
что задача (2) имеет опорное решение
![]() с единичным базисом
с единичным базисом
![]() .
Следовательно, можно использовать для
решения задачи (2) симплекс алгоритм.
При этом найти оптимальное решение или
убедиться в неограниченности целевой
функции M-задачи
можно,
не придавая M
конкретного значения.
.
Следовательно, можно использовать для
решения задачи (2) симплекс алгоритм.
При этом найти оптимальное решение или
убедиться в неограниченности целевой
функции M-задачи
можно,
не придавая M
конкретного значения.
В самом деле, и
критерий оптимальности опорного решения,
и признак неограниченности целевой
функции связаны со знаками оценок
![]() ,
вычисляемых по формуле из темы 2. Так
как среди коэффициентов целевой функции
задачи (2) есть коэффициенты вида M,
и так как M
не входит в коэффициенты ограничений,
то
,
вычисляемых по формуле из темы 2. Так
как среди коэффициентов целевой функции
задачи (2) есть коэффициенты вида M,
и так как M
не входит в коэффициенты ограничений,
то
![]() можно представить в виде:
можно представить в виде:
![]() (3)
(3)
где
![]() и
и
![]() уже не зависят от M.
Из (3) видно,
что
уже не зависят от M.
Из (3) видно,
что
 (4)
(4)
Легко видеть также,
что номер s,
для которого
![]() среди
среди
![]() ,
определяется следующим образом:
,
определяется следующим образом:
![]() для
для
![]()
или же,
если все
![]() для
для
![]() ,
то
,
то
![]() для
для
![]() .
.
Теорема 1.
Если задача (2) имеет при достаточно
больших M
неограниченную сверху на допустимом
множестве целевую функцию, то целевая
функция задачи (1) также не ограничена
сверху на допустимом множестве, если
оно не пусто. Если же задача (2) разрешима
и
![]()
некоторое её оптимальное опорное
решение, то возможны два случая:
некоторое её оптимальное опорное
решение, то возможны два случая:
-
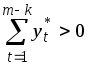 ,
тогда задача (1) не имеет допустимых
решений;
,
тогда задача (1) не имеет допустимых
решений; -
 ,
тогда вектор
,
тогда вектор
 является оптимальным опорным решением
задачи (1).
является оптимальным опорным решением
задачи (1).
Пример 1. Решить симплекс-методом каноническую задачу линейного программирования (2), где

Рассмотрим M-задачу:
![]()
![]()
![]()
![]()
![]()
Опорным решением
M-задачи
является вектор
![]() с единичным базисом
с единичным базисом
![]() .
Будем решать M-задачу
симплекс-методом. Результаты вычислений
оформляем в виде симплекс-таблиц. В
табл. 1 находится симплекс-таблица,
соответствующая опорному решению
.
Будем решать M-задачу
симплекс-методом. Результаты вычислений
оформляем в виде симплекс-таблиц. В
табл. 1 находится симплекс-таблица,
соответствующая опорному решению
![]() .
.
![]() Таблица 1
Таблица 1
|
|
№ |
Базис |
Сбаз |
A0 |
6 |
-1 |
2 |
-1 |
1 |
-M |
-M |
|
|
|
|
|
|
A1 |
A2 |
A3 |
A4 |
A5 |
A6 |
A7 |
|
|
1 |
A6 |
-M |
2 |
-1 |
"1" |
1 |
0 |
0 |
1 |
0 |
|
|
2 |
A4 |
-1 |
11 |
5 |
2 |
1 |
1 |
1 |
0 |
0 |
|
|
3 |
A7 |
-M |
6 |
3 |
2 |
0 |
0 |
1 |
0 |
1 |
|
|
4 |
- |
- |
-11 |
-11 |
-1 |
-3 |
0 |
-2 |
0 |
0 |
|
|
5 |
- |
- |
-8 |
-2 |
-3 |
-1 |
0 |
-1 |
0 |
0 |
В данной таблице
в столбце
![]() содержатся числа
содержатся числа
![]() а в 4-й и 5-й позициях этого столбца
числа
а в 4-й и 5-й позициях этого столбца
числа
![]() .
.
При этом числа
![]() определяют по формуле (3),
а числа
определяют по формуле (3),
а числа
![]() по формуле
по формуле
![]() .
.
Анализируя табл.
1,
видим,
что отрицательными оценками являются
![]() ,
причем
,
причем
![]()
наименьшая из них:
наименьшая из них:
![]() .
При этом ни для одной из отрицательных
оценок все числа соответствующего
столбца не являются неположительными.
Это означает,
что данное опорное решение не оптимально,
и нет основания утверждать, что целевая
функция задачи не ограничена сверху на
допустимом множестве. Таким образом,
вектор
.
При этом ни для одной из отрицательных
оценок все числа соответствующего
столбца не являются неположительными.
Это означает,
что данное опорное решение не оптимально,
и нет основания утверждать, что целевая
функция задачи не ограничена сверху на
допустимом множестве. Таким образом,
вектор
![]() следует ввести в базис (этот факт отмечен
стрелкой сверху). Затем ищем вектор,
который следует вывести из базиса. Для
этого находим отношения:
следует ввести в базис (этот факт отмечен
стрелкой сверху). Затем ищем вектор,
который следует вывести из базиса. Для
этого находим отношения:
![]()
Минимальное
отношение
![]() =2.
Следовательно, из базиса выводим первый
(по занимаемому месту) вектор
=2.
Следовательно, из базиса выводим первый
(по занимаемому месту) вектор
![]() .
Этот факт отмечен стрелкой слева. Ведущий
элемент
.
Этот факт отмечен стрелкой слева. Ведущий
элемент
![]() выделен жирным шрифтом и кавычками.
выделен жирным шрифтом и кавычками.
Заполняем симплекс-таблицу, соответствующую новому опорному решению. Для этого используем основные симплекс-формулы. При этом, сначала, заполняем 1-ю строку таблицы, полагая
![]()
Из табл. 2 следует,
что текущий базис не оптимальный, в
новый базис вводим вектор
![]() .
Находим отношения:
.
Находим отношения:
![]()
Следовательно,
![]() и вектор
и вектор
![]() выводим из базиса.
выводим из базиса.
![]() Таблица
2
Таблица
2
|
|
№ |
Базис |
Сбаз |
A0 |
6 |
-1 |
2 |
-1 |
1 |
-M |
-M |
|
|
|
|
|
|
A1 |
A2 |
A3 |
A4 |
A5 |
A6 |
A7 |
|
|
1 |
A2 |
-1 |
2 |
-1 |
1 |
1 |
0 |
0 |
1 |
0 |
|
|
2 |
A4 |
-1 |
7 |
7 |
0 |
-1 |
1 |
1 |
-2 |
0 |
|
¬ |
3 |
A7 |
-M |
2 |
"5" |
0 |
-2 |
0 |
1 |
-2 |
1 |
|
|
4 |
- |
- |
-9 |
-12 |
0 |
-2 |
0 |
-2 |
1 |
0 |
|
|
5 |
- |
- |
-2 |
-5 |
0 |
2 |
0 |
-1 |
3 |
0 |
Заполняем новую
симплекс-таблицу. При этом обращаем
внимание на то,
что новый базис не содержит искусственных
базисных векторов (т.е.
![]() и
и
![]() ),
а значит 5-я строка симплекс-таблицы не
нужна (она будет состоять из нулей) и
столбцы
),
а значит 5-я строка симплекс-таблицы не
нужна (она будет состоять из нулей) и
столбцы
![]() ,
,
![]() не нужны и в дальнейшем не используются.
не нужны и в дальнейшем не используются.
![]() Таблица 35
Таблица 35
|
|
№ |
Базис |
Сбаз |
A0 |
6 |
-1 |
2 |
-1 |
1 |
|
|
|
|
|
|
A1 |
A2 |
A3 |
A4 |
A5 |
|
|
1 |
A2 |
-1 |
12/5 |
0 |
1 |
3/5 |
0 |
1/5 |
|
¬ |
2 |
A4 |
-1 |
21/5 |
0 |
0 |
"9/5" |
1 |
-2/5 |
|
|
3 |
A1 |
6 |
2/5 |
1 |
0 |
-2/5 |
0 |
1/5 |
|
|
4 |
- |
- |
-21/5 |
0 |
0 |
-34/5 |
0 |
2/5 |
|
|
|
|
|
|
|
|
|
|
¯ |
|
¬ |
1 |
A2 |
-1 |
1 |
0 |
1 |
0 |
-1/3 |
"1/3" |
|
|
2 |
A3 |
2 |
7/3 |
0 |
0 |
1 |
5/9 |
-2/9 |
|
|
3 |
A1 |
6 |
4/3 |
1 |
0 |
0 |
2/9 |
1/9 |
|
|
4 |
- |
- |
35/3 |
0 |
0 |
0 |
34/9 |
-10/9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
A5 |
1 |
3 |
0 |
3 |
0 |
-1 |
1 |
|
|
2 |
A3 |
2 |
3 |
0 |
2/3 |
1 |
1/3 |
0 |
|
|
3 |
A1 |
6 |
1 |
1 |
-1/3 |
0 |
1/3 |
0 |
|
|
4 |
- |
- |
15 |
0 |
10/3 |
0 |
8/3 |
0 |
Указанный факт
означает, что получено опорное решение
непосредственно исходной задачи и
дальнейшие итерации симплекс-метода
состоят в его улучшении (т.е. решается
непосредственно исходная, а не M-задача).
Из табл. 3 следует,
что все оценки
![]() неотрицательны,
а значит на 4-й итерации симплекс-метода
получено оптимальное опорное решение
x*
= (1, 0, 3, 0, 3), а оптимум
l*
= 15. Заметим, что нулевые оценки в последней
таблице соответствуют только базисным
векторам. Откуда следует единственность
оптимального опорного решения в данной
задаче.
неотрицательны,
а значит на 4-й итерации симплекс-метода
получено оптимальное опорное решение
x*
= (1, 0, 3, 0, 3), а оптимум
l*
= 15. Заметим, что нулевые оценки в последней
таблице соответствуют только базисным
векторам. Откуда следует единственность
оптимального опорного решения в данной
задаче.
Задание. В задачах 3.1 3.102 для заданных
 ,
,
 и
и
![]() решить симплекс-методом
каноническую задачу линейного
программирования
решить симплекс-методом
каноническую задачу линейного
программирования
![]() ;
;
![]()
![]()
![]()
|
3.1 A=; B=.
|
3.2 A=; B=.
|
|
3.3 A=; B=.
|
3.4 A=; B=.
|
|
3.5 A=; B=.
|
3.6 A=; B=.
|
