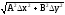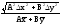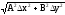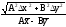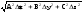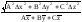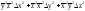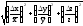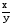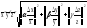Lab1

Лабораторная работа №1

ОПРЕДЕЛЕНИЕ ЛИНЕЙНЫХ РАЗМЕРОВ И ПЛОТНОСТИ ТЕЛ, ОЦЕНКА

ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЙ

Цель работы ‑ измерение линейных размеров тел с помощью штангенциркуля и микрометра, изучение методики оценки погрешностей измерений, определить плотности тел правильной геометрической формы по данным измерений их линейных размеров и масс.

Приборы и принадлежности

Тела равного веса (цилиндрической формы), штангенциркуль, микрометр.

Краткая теория

Приборы для измерения линейных размеров тел

1. Нониус

Для измерения длины необходимо иметь масштаб, то есть линейку с делениями. Измеряемое тело прикладывается одним концом к нулю масштабной линейки; если при этом противоположный конец тела оказывается между m и (m+1) миллиметров делениями линейки, то это значит, что длина тела L больше m и меньше (m+1) мм:

m < L < (m+1) (мм).

Для более точного измерения длины тела масштаб должен быть снабжён нониусом. Нониус представляет собой линейку, передвигающуюся вдоль масштаба. Цена деления нониуса отличается от цены деления масштаба. Обычно она подбирается следующим образом: берут (n-1) делений масштаба и приравнивают их n делениям нониуса, так что каждое деление нониуса составляет (n-1)/n часть деления масштаба. Например, если n = 10, то каждое деление нониуса составляет 0,9 делений шкалы, 0,9 мм для миллиметрового масштаба.

Пусть правый конец измерительного тела AB находится между 15 и 16 делениями масштаба. Плотно придвинув к этому концу тела нониус, определяем, что седьмое деление нониуса совпадает с одним из делений масштаба.

Найдём теперь избыток (Х) длины тела АВ сверх целых 15 единиц масштаба. Для этого, прежде всего, отметим, что расстояние между 15-м делением масштаба, показывающим целое число делений масштаба, укладывающихся на длине тела АВ, и делением масштаба, совпадающим с делением нониуса (на рис.1, см. примечание 1, это расстояние обозначено СД) с одной стороны равно 7 делениям масштаба, а с другой стороны 7 делениям нониуса плюс Х, то есть 7 делений масштаба равно 7 делениям нониуса плюс Х, откуда Х = 7 дел. масштаба – 7 дел. нониуса.

Если масштаб-миллиметровая линейка и n = 10, то цена деления нониуса 0,9 мм и Х = 7 мм – 7 мм  0,9 мм = 0,7 мм.

Длина тела АВ L = 15,7 мм.

Обозначим цену деления масштаба Х, а цену деления нониуса у. Величина

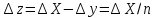
носит название точности нониуса, она представляет максимальную погрешность нониуса.

В любом положении нониуса относительно масштаба одно из делений первого совпадает с каким-либо делением второго.

Длина отрезка, измеряемого при помощи нониуса, равна числу целых делений масштаба плюс точность нониуса, умноженная на номер деления нониуса, совпадающего с некоторым делением масштаба.

2. Штангенциркуль

На примере нониуса основано устройство прибора, называемого штангенциркулем. Масштабная линейка R имеет выступ в виде ножки N, оканчивающейся острием. Рама, снабжённая выступом в виде второй ножки T, передвигается вдоль масштабной линейки, часть её служит нониусом. Измеряемое тело зажимается между ножками N и Т. Когда ножки сдвинуты, нуль нониуса совпадает с нулём масштаба. Измеряемое тело зажимается между ножками N и Т. измеряемая длина равна расстоянию между нулём масштабной линейки и нулём нониуса.

3. Микрометр

При точных измерениях расстояний нередко применяются микрометрические винты – винты с малым и точно выдержанным шагом. Такие винты используются, например, в микрометрах.

Подвижный стержень представляет собой конец винта. При каждом новом обороте винт передвигается на 0,5 мм – одно деление линейной шкалы на корпусе. С винтом связан барабан с круговой шкалой, содержащей 50 (или иное число) равных делений.

Так как один полный оборот барабана соответствует передвижению винта на 0,5 мм, то поворот барабана на одно деление перемещает винт на 0,01 мм.

Результат измерений складывается из показаний линейной шкалы на корпусе и показаний шкалы барабана.

Рукоятка микрометра снабжена "трещёткой", ограничивающей давление винта на измеряемое тело допустимым по ГОСТУ значением.

Измерения с помощью микрометра производятся с погрешностью, не превышающей 0,01 мм.

Классификация погрешностей измерения:

Измерения делятся на прямые и косвенные. Измерения, при которых физическая величина определяется непосредственно с помощью приборов, называются прямыми. Примеры прямых измерений: определение линейных размеров тел с помощью масштабной линейки, штангенциркуля или микрометра, взвешивание тел, измерение времени секундомером.

Чаще приходится вычислять искомую величину по формулам, включающим физические величины, получаемые прямыми измерениями. Такие измерения называются косвенными. Примеры косвенных измерений могут служить измерения объёмов тел. Объём параллелепипеда (V) вычисляется по формуле V = a  b  c, где а, b, с – длина, ширина и высота бруска – величины, получаемые путём прямых измерений, например, штангенциркулем.

Любые измерения производятся с некоторыми погрешностями (ошибками измерений).

Погрешности, возникающие вследствие недосмотра, грубых ошибок экспериментатора или неисправности аппаратуры называются промахи. Результаты измерений, содержащие грубые погрешности (промахи), отбрасываются.

Не связанные с грубыми ошибками погрешности делятся на случайные и систематические.

Погрешности, меняющие величину и знак от опыта к опыту, называют случайными. Случайные погрешности могут быть связаны с несовершенством объекта измерений, например, при измерении диаметра проволоки – она из-за случайных причин, возникающих при изготовлении, имеет не вполне круглое сечение, что приводит к разбросу повторных измерений её диаметра. Из-за не вполне правильной формы получаются несколько различные значения длины, ширины и высоты параллелепипеда при повторных измерениях. Типичным примером случайных погрешностей может служить так называемая ошибка параллакса: отсчёт делений шкалы прибора (например, нониуса) зависит от положения глаза экспериментатора. Случайные погрешности могут быть связаны с трением в приборах. Так стрелка измерительного прибора будет останавливаться не на "правильном" делении, а вблизи него то справа, то слева. При взвешивании случайные погрешности возникают в результате сотрясения основания весов при движении городского транспорта, от сквозняков и т.д.

Погрешности, сохраняющие свою величину и знак во время экспериментов, называют систематическими. Они могут быть связаны с неправильной шкалой прибора, неравномерным шагом микрометрического винта, не равными плечами весов. Систематические ошибки могут быть связаны с методом измерений. Например, если при взвешивании тела не учитывать действия выталкивающей силы воздуха, мы будем всё время получать заниженные результаты взвешивания. Округляя численную величину до какого-то приближённого значения, например, полагая  =3;  =3,1;  = 3,14;  = 3,1416; и т.д. вместо  = 3,14159265…мы допускаем систематическую погрешность.

К систематическим ошибкам приводит неправильная установка прибора, например, неопытный экспериментатор не отрегулировал "нуль", поставил весы вблизи трубы отопления, что привело к неодинаковому нагреву левого и правого плеча коромысла весов. В результате систематических погрешностей имеющие разброс из-за случайных ошибок результаты опыта колеблются не вокруг истинного, а вокруг некоторого смещённого значения.

Погрешность, вносимая измерительным прибором при каждом отдельном измерении, называется приборной погрешностью. Приборная погрешность содержит в себе как систематические, так и случайные погрешности. К систематическим погрешностям можно отнести погрешности, связанные со смещением начала отсчёта шкалы, с неравномерностью нанесения штрихов шкалы и т.п. Из случайных погрешностей в состав приборной погрешности входят погрешности, возникающие под действием силы трения в отдельных частях прибора, из-за движения частей прибора друг относительно друга в зазорах (люфт) и т.д.

Выявление систематических погрешностей измерительных приборов производится с помощью эталонных приборов и требует тщательных метрологических исследований. Поэтому в обычной лабораторной практике приборную ошибку приближённо считают случайной ошибкой, характерной для партии данных приборов в условиях их массового производства.

Абсолютной погрешностью измерений называют разность между найденным на опыте и истинным значением физической величины.

Относительной погрешностью измерений называют отношение абсолютной погрешности к значению измеряемой величины.

Так как обычно истинное значение измеряемой физической величины неизвестно, точно вычислить абсолютную и относительную погрешности измерений невозможно. При практических измерениях погрешности не вычисляются. Приёмы оценки погрешностей обосновываются теорией вероятностей и математической статистикой и изложены во многих пособиях и руководствах. Список некоторых из них приведён в конце описания.

Мы приводим здесь лишь краткие рекомендации по оценке случайных погрешностей при прямых измерениях.

Порядок выполнения работы

Оценка погрешностей прямых измерений:

Обозначим истинное значение (нам известное) измеряемой величины "Х ".

1. Проведите n измерений.

2. Результаты измерений Х₁, Х₂, Х₃, … Х_n заносятся в таблицу.

3. В качестве наилучшего значения для измеряемой величины принимается среднее арифметическое из всех полученных результатов. Среднее значение нескольких величин Х обозначается <X>. Таким образом:

.

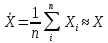4. Находятся погрешности отдельных измерений

.

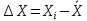5. Вычисляют квадраты погрешностей отдельных измерений .

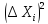6. Если одно (или несколько) измерений резко отличаются по своему значению от остальных значений, то следует проверить не является ли оно промахом. Если это промах, его следует отбросить.

7. Определяется средняя квадратичная погрешность результата 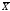серии n измерений

.

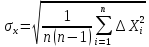8. Задаётся значение надёжности Р измерений. Количественно надёжность измерений определяется вероятностью того, что результат измерений 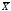отличается от истинного значения Х на величину, не большую Х.

Интервал значений 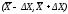, в котором с заданной надёжностью можно обнаружить значение измеряемой величины, называется доверительным интервалом.

Очевидно, что величина доверительного интервала и надёжности взаимозависимы. Чем ближе Р к единице, тем шире оказывается доверительный интервал.

Следовательно, при практическом вычислении абсолютной ошибки результата измерений необходимо заранее условиться о величине надёжности, задать её. Надёжность задаётся, исходя из следующих соображений. При больших Р из-за увеличения Х теряется представление даже о порядке измеряемой величины. Поэтому брать Р очень близким к 1 нецелесообразно. При физических измерениях считается достаточной надёжность Р = 0,95.

9. Находятся границы доверительного интервала (погрешность результата измерений).

В математической статистике показывается, что при вычислениях доверительного интервала следует различать два случая.

Если число измерений

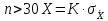
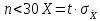
Здесь К – коэффициент для нормального распределения, t – коэффициенты Стьюдента, вычисляемые по законам теории вероятностей. Их значение для разных n и Р приведены в таблицах 1 и 2 (см. приложение 2).

10. Определяется предельная погрешность используемого измерительного прибора (). Приборную погрешность обычно приравнивают равной 0,5 цены его деления. Для современных приборов погрешность указывается в паспорте.

Приборная погрешность электроизмерительных приборов вычисляется по их классу точности ( ):

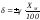
где Х_М – значение измеряемой величины соответствующее перемещению стрелки на всю шкалу.

Доверительный интервал соответствующий приборной ошибке, определяется при заданной надёжности Р по формуле:

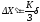
где К – коэффициент из таблицы 1.

В таблице 3 (см. приложение 2) приведены погрешности некоторых простейших лабораторных приборов.

11. Если величина погрешности результата измерений (определяемая в п.9 ) окажется сравнимой с величиной погрешности прибора, то в качестве границы доверительного интервала следует взять величину:

.

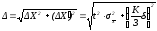12. Окончательный результат записывается в виде:

.

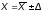13. Оценивается относительная погрешность результатов серии измерений:

%.

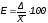Оценка погрешностей косвенных измерений:

Пусть искомая величина U определяется из прямых измерений величин x, y, z, …причём в этом случае погрешность результата определяется следующим образом.

1. Для каждой серии измерений величин x, y, z, …, входящих в определение искомой величины, проводится обработка, как описано в п.3. При этом для всех измеренных величин задают одно и то же значение надёжности Р.

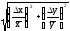
2. Находятся выражения для абсолютной и относительной погрешностей искомой величины U в соответствии с конкретным видом её функциональной зависимости от x, y, z, …, так как абсолютные погрешности много меньше измеряемых величин, их можно считать приблизительно равными дифференциалам:   dx,   dy,   dz, U  dU. Относительная погрешность косвенно измеряемой величины U может быть представлена через дифференциал логарифма:

.

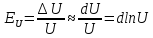Поэтому, если зависимость U = U( x, y, z,…) включает произведение, то для нахождения E_U надо прологарифмировать выражение, а затем взять производную обеих частей и найти искомую относительную ошибку.

Если зависимость U = U(x, y, z,…) включает сумму, удобнее без предварительного логарифмирования искать путём дифференцирования абсолютную погрешность U.

В таблице 4 (см. приложение 1) приведены ошибки различных встречающихся в лабораторной практике функций.

3. Оцениваются границы доверительного интервала для результата косвенных измерений. При этом используется либо формула:

где 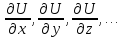вычисляются при 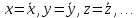, либо по одной из формул из таблицы 4 (см. приложение).

4. Определяется относительная погрешность результата серии косвенных измерений:

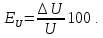
Содержание отсчёта

Письменный отсчёт по лабораторной работе должен содержать рисунки и формулы, разъясняющие действия нониуса, порядок (по пунктам) оценки погрешностей при прямых измерениях, таблицы результатов измерений, вычисления погрешностей прямых и косвенных измерений при определении объёма.

При защите необходимо знать определения, связанные с обработкой результатов.

Контрольные вопросы

1.        Каков принцип измерения нониусом?

2.        Как производятся измерения штангенциркулем и микрометром?

3.        Что такое измерение и точность измерения?

4.        Измерения прямые и косвенные, каковы их отличия?

5.        Какие существуют типы погрешностей (ошибок)?

6.        Какую погрешность называют промахом?

7.        Дайте определения абсолютной и относительной погрешности.

8.        Что называется доверительным интервалом?

9.        Какая связь существует между систематической и случайной ошибкой?

Список рекомендуемой литературы

1. Методика организации и проведения физического эксперимента (механика и молекулярная физика). Метод. указания, Краснодар.

2. М.Г. Брик, И.Д. Брегеда, М.П. Матвеякин. Методы обработки результатов эксперимента в лабораторном физическом практикуме. Учебное пособие. Краснодар, 1997.

3. О.Н. Касандрова, В.В. Лебедев. Обработка результатов наблюдений. Наука, М.: 1971.

4. Дж. Сквайрс. Практическая физика. М.: 1971.

5. Лабораторные занятия по физике. Под ред. Л.Л. Гольдина, М.: Наука, 1983.

Приложения

Приложение 1

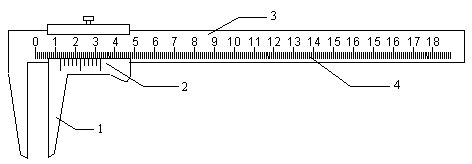
Рис. 1. Штангенциркуль:1 – губки; 2 – шкала нониуса; 3 – штанга;

4 – основная шкала.

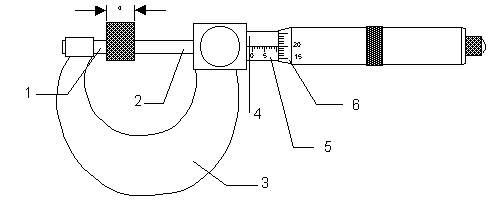
Рис. 2. Микрометр: 1 – пятка; 2 – шпиндель с микрометрическим винтом; 3 – скоба; 4 – стебель; 5 – основная шкала; 6 – шкала барабана.

Приложение 2

Таблица1. Коэффициенты нормального распределения

Р	0,5	0,63	0,75	0,8	0,9	0,95	0,99
К	0,7	1,00	1,15	1,3	1,7	2,00	2,60

Таблица 2. Коэффициент Стьюдента

Р n - 1	0,5	0,7	0,8	0,9	0,95	0,98	0,99
1	1,0	2,0	3,1	6,3	1,3	3,2	6,4
2	0,8	1,3	1,9	2,9	4,3	7,0	9,9
3	0,7	1,3	1,6	2,4	3,2	4,5	5,8
4	0,7	1,2	1,5	2,1	2,8	3,7	4,6
5	0,7	1,2	1,5	2,0	2,6	3,4	4,0
6	0,7	1,1	1,4	1,9	2,4	3,1	3,7
7	0,7	1,1	1,4	1,9	2,4	3,0	3,5
8	0,7	1,1	1,4	1,9	2,3	2,9	3,4
9	0,7	1,1	1,4	1,8	2,3	2,8	3,3
10	0,7	1,1	1,4	1,8	2,2	2,8	3,2
15	0,7	1,1	1,3	1,8	2,1	2,6	2,9

Таблица 3. Погрешности некоторых приборов

Название прибора	Цена деления		Погрешность
Штангенциркуль	0,10 мм		0,050 мм
	0,05 мм		0,025 мм
Микрометр	0,01 мм		0,005 мм
Деревянная линейка	1,00 мм		0,500 мм
Пластмассовая линейка	1,00 мм		0,500 мм
Технические разновесы	100 г 10 г 1 г 10 – 500 мг 1 мг		2,0 мг 2,0 мг 1,0 мг 0,5 мг 0,1 мг
Электроизмерительные приборы	Класс точности, Х пред. знач. шкалы делённое на 100
Лабораторные термометры	10С	0,50С

Таблица 4. Приближённое определение погрешностей функций нескольких переменных

Вид функции: U=U(x,y,z,…)	Абсолютная погрешность: U	Относительная погрешность: EU = U/U
Ax+By A=const, B=const
Ax - By
Ax + Ay + Cz
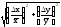
xy
xyz
Вид функции: U=U(x,y,z,…)	Абсолютная погрешность: U	Относительная погрешность: EU = U/U
x y z