
3a
.pdf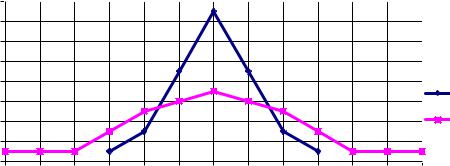
Тема: «ОЦЕНКА РАЗНООБРАЗИЯ КОЛИЧЕСТВЕННОГО ПРИЗНАКА»
Напомним, что для описания статистической совокупности по качественному (описательному, атрибутивному) признаку рассчитывают относительные показатели. С ними мы познакомились на первом занятии 6-го семестра.
Для описания совокупности по количественному признаку выполняют следующие виды работы:
определяют среднее значение признака (или другими словами «центральную тенденцию ряда»),
оценивают характер распределения,
оценивают разнообразие (вариабельность) признака.
Вариационный ряд (ряд распределения) и средние величины были темой второго занятия в
данном семестре. Третье занятие посвятим изучению того, что такое разнообразие (вариабельность) количественного признака и как можно его охарактеризовать.
Сравним два вариационных ряда (таблицы 1 и 2, рисунок 1). Для удобства анализа пусть оба ряда будут абсолютно симметричными.
|
Таблица 1 |
Вариационный ряд «А» |
|
|
|
Варианта (V) |
Частота (Р) |
17 |
1 |
18 |
3 |
19 |
9 |
20 |
15 |
21 |
9 |
22 |
3 |
23 |
1 |
|
n1= Рi=41 |
|
Таблица 2 |
Вариационный ряд «В» |
|
|
|
Варианта (V) |
Частота (Р) |
14 |
1 |
15 |
1 |
16 |
1 |
17 |
3 |
18 |
5 |
19 |
6 |
20 |
7 |
21 |
6 |
22 |
5 |
23 |
3 |
24 |
1 |
25 |
1 |
26 |
1 |
|
n2= Рi=41 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 1 |
|
Вариационные ряды с разной величиной разнообразия признака |
||||||||||||
|
16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
14 |
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
Р |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
Частота, |
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
Ряд "А" |
|
6 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
4 |
|
|
|
|
|
|
|
|
|
|
|
Ряд "В" |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
|
|
|
|
|
|
Варианта, V |
|
|
|
|
|
||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
Нетрудно заметить, что ряды «А» и «В» в чем-то похожи:
Оба ряда состоят из одинакового числа наблюдений (n1 = n2 = 41), поэтому площадь под линией распределения одинаковая.
Средний размер изучаемого признака в обоих рядах тоже одинаков и равен 20. Поскольку оба ряда являются симметричными, то в каждом из них мода, медиана и среднее арифметическое совпадают: Мо1 = Мо2 = Ме1 = Ме2 = М1 = М2 = 20
Вто же время ряды выглядят разными:
Ряд «А» почти в два раза короче, чем ряд «В» (в ряду «А» число вариант равно 7, а в ряду «В» равно 13)
Линия распределения «А» более высокая (варианты «сгруппировались», «скучились» около среднего значения), а линия распределения «В» более низкая, пологая (варианты «рассыпались» далеко от средней величины)
Отличия рядов обусловлены разной величиной вариабельности (разнообразия).
Следовательно, для того, чтобы описать распределение количественного признака в изучаемой совокупности, расчета среднего значения будет совершенно недостаточно. Необходимо также оценить разнообразие признака.
Основными показателями, которые характеризуют, описывают разнообразие, вариабельность признака (разброс вариант), являются:
I.Амплитуда (Ampl)
II.Лимит (lim)
III.Дисперсия (D)
IV. Среднеквадратическое (стандартное) отклонение (σ)
V. Коэффициент вариации (CV)
VI. Квантили
I. АМПЛИТУДА
Амплитуда (размах) представляет собой разность максимального (Vmax) и минимального (Vmin) значений признака в изучаемой совокупности.
В примере с изучением массы тела студентов (Тема «Вариационный ряд и средние величины») амплитуда будет равна:
Вариационные ряды «А» и «В», приведенные в начале учебного материала к занятию, характеризуются амплитудой (размахом):
Ряд «А»:
Ряд «В»:
Как видим, ряд «В» характеризуется большим разнообразием признака. Его амплитуда (размах) в два раза больше, чем в ряду «А».
II. ЛИМИТ
Лимит представляет собой соотношение максимального (Vmax) и минимального (Vmin) значений признака в изучаемой совокупности.
В примере с изучением массы тела студентов (Тема «Вариационный ряд и средние величины») лимит будет равен:
2
Вариационные ряды «А» и «В», приведенные в начале учебного материала к занятию, характеризуются лимитом:
Ряд «А»: Ряд «В»:
Ряд «В» характеризуется большим разнообразием признака – его максимальное значение в 1,86 раза больше минимального (в ряду «А» – только в 1,35 раза).
III. ДИСПЕРСИЯ
Существенным недостатком амплитуды и лимита как критериев вариабельности является то, что они полностью зависят от крайних значений признака и никак не учитывают значения признака внутри ряда. Сравним два следующих распределения (таблицы 3 и 4, рисунок 2):
Таблица 3
Вариационный ряд «К»
Варианта (V) |
Частота (Р) |
15 |
1 |
16 |
2 |
17 |
3 |
18 |
5 |
19 |
6 |
20 |
7 |
21 |
6 |
22 |
5 |
23 |
3 |
24 |
2 |
25 |
1 |
|
n2=Рi=41 |
Таблица 4
Вариационный ряд «М»
Варианта (V) |
Частота (Р) |
15 |
1 |
16 |
1 |
17 |
1 |
18 |
2 |
19 |
3 |
20 |
25 |
21 |
3 |
22 |
2 |
23 |
1 |
24 |
1 |
25 |
1 |
|
n2=Рi=41 |
|
|
|
|
|
|
|
|
|
|
|
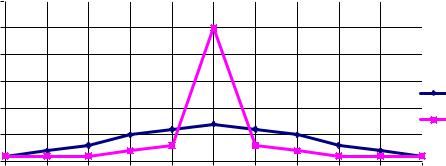
Рисунок 2 |
Вариационные ряды с одинаковой амплитудой и разной величиной разнообразия признака |
|||||||||||
|
30 |
|
|
|
|
|
|
|
|
|
|
|
25 |
|
|
|
|
|
|
|
|
|
|
Р |
20 |
|
|
|
|
|
|
|
|
|
|
Частота, |
15 |
|
|
|
|
|
|
|
|
|
Ряд "К" |
10 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
Ряд "М" |
||
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
|
|
|
|
|
|
Варианта, V |
|
|
|
|
|
Как видим, минимальное и максимальное значения в вариационных рядах «К» и «М» |
|||||||||||
совпадают (Vmin=15 и Vmax=25). Следовательно, оба ряда будут иметь |
|
|
|||||||||
одинаковую амплитуду: AmplK = AmplM = Vmax – Vmin= 25 – 15 = 10 |
|||||||||||
одинаковый лимит: limK = limM = 25 ÷ 15 = 1,67 |
|
|
|
|
|||||||
Однако если учесть не только крайние значения, но и значения признака внутри ряда, то увидим, что |
|||||||||||
ряд «М», скорее всего, является менее разнообразным – ведь там более половины единиц |
|||||||||||
наблюдения имеют одинаковое значение признака, равное 20. |
|
|
|
|
|||||||
3

Самым широко используемым показателем разнообразия является дисперсия (от лат. dispersion – рассыпанный). Она позволяет учесть не только крайние значения признака, но и все значения, присутствующие в ряду (варианты, V), а также частоту встречаемости этих значений (Р).
Чтобы рассчитать дисперсию, сначала вычисляют отклонения всех вариант от среднего арифметического (di):
Чтобы охарактеризовать весь вариационный ряд, следовало бы суммировать все значения di. Однако этого делать нельзя. Почему же? По той простой причине, что для вариант (Vi), которые больше среднего арифметического (М) величина di получится положительным числом, а для вариант, которые меньше среднего арифметического – отрицательным. При суммировании положительных и отрицательных величин они будут друг друга взаимно компенсировать, и мы не сможем получить характеристику разнообразия признака. Поэтому сначала все отклонения от среднего (di) возводят в квадрат (di2), потом суммируют и делят на число наблюдений, т.е. находят среднее арифметическое этих величин – средний квадрат отклонений или дисперсию (D). Чем больше дисперсия, тем больше разнообразие признака.
В простом вариационном ряду дисперсию рассчитывают по формуле:
∑
Если ряд развернутый, то учитывают не только числовые значения признака (V), но и частоту их встречаемости (Р). Каждый квадрат отклонения (di2) «взвешивают», т.е. умножают на соответствующую частоту (Рi)
∑
[ ]
В статистике существует понятие «малая выборка». Большинство авторов малой называют выборку, содержащую менее 30 единиц наблюдения. При расчете дисперсии для малой выборки некоторые авторы рекомендуют в формулу вносить поправку – уменьшать знаменатель на единицу, чтобы при последующем анализе ориентироваться на большее разнообразие признака:
∑
[ ]
Вэлектронной таблице Microsoft Excel формула [1] используется для расчета дисперсии в генеральной совокупности (статистическая функция ДИСПР), а формула [2] – для расчета дисперсии по выборке (статистическая функция ДИСП).
Вкачестве примера рассчитаем дисперсию массы тела для выборки из 55 студентовпервокурсников (задача из темы «Вариационный ряд и средние величины»). Средняя масса тела (М) была равна 60,7 кг. Алгоритм расчета дисперсии представлен в таблице 5.
|
|
|
|
|
|
|
Таблица 5 |
|
|
|
Пример расчета дисперсии |
|
|
|
|
||
Варианта, V |
Частота, Р |
di = Vi – М |
|
di2 |
di2 * Рi |
|
||
(масса тела, кг) |
(абс. числа) |
|
|
|
|
|
|
|
57 |
3 |
57 – 60,7= –3,7 |
–3,72 |
= 13,69 |
13,69 * 3 |
= 41,07 |
|
|
58 |
6 |
58 – 60,7 = –2,7 |
–2,72 = 7,29 |
7,29 * 6 = 43,74 |
|
|||
59 |
7 |
59 – 60,7 = –1,7 |
–1,72 = 2,89 |
2,89 * 7 = 20,23 |
|
|||
60 |
11 |
60 – 60,7 = –0,7 |
–0,72 = 0,49 |
0,49 * 11 = 5,39 |
|
|||
61 |
9 |
61 – 60,7 = 0,3 |
0,32 |
= 0,09 |
0,09 |
* 9 |
= 0,81 |
|
62 |
7 |
62 – 60,7 = 1,3 |
1,32 |
= 1,69 |
1,69 * 7 = 11,83 |
|
||
63 |
7 |
63 – 60,7 = 2,3 |
2,32 |
= 5,29 |
5,29 * 7 = 37,03 |
|
||
64 |
4 |
64 – 60,7 = 3,3 |
3,32 = 10,89 |
10,89 |
* 4 |
= 43,56 |
|
|
65 |
1 |
65 – 60,7 = 4,3 |
4,32 = 18,49 |
18,49 |
* 1 |
= 18,49 |
|
|
|
n=Рi=55 |
|
|
|
di2 * Рi = 222,15 |
|
||
Далее выполним расчет дисперсии по уже известной нам формуле. Используем формулу [1], т.е. формулу без поправки знаменателя, т.к. наша выборка не является малой (n=55>30).
4

∑
Теперь перед нами возникает вопрос: в каких же единицах измеряется дисперсия? Отклонение от среднего (di) измеряется в абсолютных именованных величинах (тех же, что и количественный признак) – килограммах, сантиметрах, днях, ммоль/л и пр. Затем di мы возводим в квадрат.
Следовательно, дисперсия измеряется в абсолютных именованных величинах, возведенных в квадрат – килограммы2, сантиметры2, дни2, ммоль/л2 и пр. В нашем примере с массой тела студентов-первокурсников дисперсия равна 4,04 кг2.
Оценим разнообразие признака по величине дисперсии в вариационных рядах «А» и «В», с которых мы начинали рассмотрение данной темы (таблицы 1 и 2, рисунок 1).
Дисперсия ряда «А» равна: DА = 1,5
Дисперсия ряда «В» равна: Dв = 6,5
Как видим, чем меньше разнообразие признака, тем меньше дисперсия (1,5 против 6,5). Кроме того о разнообразии можно визуально судить по форме кривой распределения – чем меньше
дисперсия, тем выше и уже «колокол» кривой. При увеличении разнообразия признака, при увеличении дисперсии (рассеяния) кривая распределения становится все более низкой и плоской.
Теперь оценим разнообразие признака по величине дисперсии в вариационных рядах «К» и «М» (таблицы 3 и 4, рисунок 2). Эти ряды характеризовались одинаковой амплитудой (размахом),
равной 10 (AmplK = AmplM = Vmax – Vmin= 25 – 15 = 10). Однако в ряду «К» единицы наблюдения были достаточно равномерно «рассыпаны» между наименьшим и наибольшим значениями (кривая
распределения была плоская, пологая). А в ряду «М» более половины наблюдений имели одинаковое срединное значение, равное 20 (кривая распределения «выскакивала» вверх высоким пиком). И действительно, дисперсия ряда «К» оказалась больше, чем дисперсия ряда «М»:
Дисперсия ряда «К» равна: DК = 5,5
Дисперсия ряда «М» равна: DМ = 3,1
Как видим, дисперсия, учитывающая все значения признака в ряду, является более «надежным» и «полноценным» показателем разнообразия, чем амплитуда и лимит, которые учитывают только крайние значения.
IV. СРЕДНЕКВАДРАТИЧЕСКОЕ (СТАНДАРТНОЕ) ОТКЛОНЕНИЕ
Недостатком дисперсии являются очень неудобная, какая-то совершенно немыслимая единица исчисления – квадрат абсолютных именованных величин, в которых измерен признак (кг2, дни2 и пр.). Поэтому большее применение находит другой показатель – среднеквадратическое отклонение (авторы часто его называют стандартное отклонение). Оно обозначается малой греческой буквой «сигма» (σ) и рассчитывается как квадратный корень из дисперсии:
√
Для простого ряда:
√√∑
Для взвешенного (развернутого) ряда:
√√∑
Для взвешенного (развернутого) ряда с малым числом наблюдений (n<30):
√√∑
Среднеквадратическое (стандартное) отклонение исчисляется в тех же единицах, что и сам измеряемый признак (килограммах, метрах, днях и пр.)
5

Произносить и писать слова «среднеквадратическое отклонение» или «стандартное отклонение» долго и неудобно. Поэтому многие авторы учебников и пособий по статистике часто называют его просто – «сигма». Ряд авторов, говоря о разнообразии признака, предпочитают использовать короткое слово «дисперсия» и писать «σ2». Также не следует удивляться, увидев в описании формулы, где фигурирует среднеквадратическое отклонение (σ), слово «дисперсия».
Рассчитаем среднеквадратическое (стандартное) отклонение для нашего примера с изучением массы тела студентов-первокурсников (задача из темы «Вариационный ряд и средние величины»):
√√
При описании полученных в исследовании результатов рекомендуется одновременно указывать и среднее значение признака (среднее арифметическое), и характеристику его разнообразия (среднеквадратическое отклонение) по схеме М±σ. Однако сначала в тексте нужно обязательно отметить это обстоятельство. Дело в том, что похожая схема представления результатов используется при интервальной оценке свойств генеральной совокупности (при указании доверительного интервала), а именно М±2m (это мы рассмотрим в рамках темы 4 «Доверительный интервал»). В нашем примере по изучению физического развития студентов фраза в статье может звучать так: «Средняя масса тела студентов-первокурсников составила 60,7±2,0 кг (здесь и далее представлены среднее арифметическое и стандартное отклонение по схеме М±σ )».
Среднее арифметическое и среднеквадратическое (стандартное) отклонение играют огромную роль в параметрическом статистическом анализе. Чтобы понять это, нам надо познакомиться с теоретическим нормальным распределением Гаусса.
Теперь немного совершенно скучной, но необходимой теории.
НОРМАЛЬНОЕ (ГАУССОВО) РАСПРЕДЕЛЕНИЕ
Распределение количественного признака, полученное в результате исследования (вариационный ряд), часто называют эмпирическое распределение (т.е. полученное на практике, опытным путем). Эмпирическое распределение исследователю обязательно надо сопоставить с тем или иным теоретическим распределением вероятности. Зачем? Если мы выясним, что наше эмпирическое распределение очень похоже на то или иное теоретическое распределение вероятности, то значит, наши математические знания об этом теоретическом распределении мы сможем использовать для ответа на многочисленные практические вопросы, связанные с эмпирическими данными. Другими словами, тогда мы сможем смело применять математические формулы, характеризующие данное теоретическое распределение вероятности, к нашему эмпирическому распределению и получать высоконадежные утверждения и выводы.
Каждое теоретическое распределение вероятности имеет математическое описание в форме уравнения, а также наглядно может быть представлено в виде кривой – функции плотности распределения вероятности (ФПРВ). Сразу же скажем «для поддержания духа»: математические уравнения, описывающие теоретические распределения вероятностей, знают только самые «продвинутые» специалисты, «помешанные» на нюансах математического анализа. Исследователю нужно знать только основные понятия, условия применения тех или иных методов, а также, какие выводы можно сделать на основании полученных результатов анализа.
Во всех наших учебных примерах мы наблюдали, что с наибольшей частотой (Р) встречаются срединные значения признака, а малые и большие значения встречаются реже. Причем, чем дальше значение признака от середины (в меньшую или в большую сторону), тем меньше частота его встречаемости. Абсолютное большинство эмпирических распределений выглядит точно так же. Такие же особенности характерны для теоретического нормального распределения. Часто его
6

называют Гауссово распределение в честь великого немецкого математика Иоганна Карла Фридриха Гаусса (1777-1855), описавшего соответствующую функцию1:
√
График Гауссова распределения представлен на рисунке 3.
Рисунок 3
Нормальное (Гауссово) распределение
Основные характеристики кривой нормального (Гауссова) распределения:
1)Форма кривой напоминает колокол (кривая унимодальная, т.е. с одной вершиной)
2)Кривая симметрична относительно среднего. Среднее, мода и медиана в нормальном распределении равны.
3)Место расположения кривой определяется средним значением. Обычно его обозначают малой греческой буквой «мю» (μ). Кривая сдвигается вправо, если средняя увеличивается, и влево, если средняя уменьшается.
4)Форма кривой определяется дисперсией (σ2) (точно так же можно сказать, что стандартным отклонением σ). Кривая становится более низкой и широкой, если дисперсия увеличивается, и наоборот – более высокой и узкой, если дисперсия уменьшается.
Последние два пункта иллюстрирует рисунок 4.
Рисунок 4
Нормальное (Гауссово) распределение при различных средних (μ) и дисперсиях (σ2)
1 Уравнение запоминать не надо!!!
7
Как видим из рисунка 4, красная, зеленая и синяя кривые характеризуются одинаковыми средними (μ=0) и поэтому имеют одинаковое расположение над горизонтальной осью. Однако у них различная форма. Красная кривая с самой маленькой дисперсией (σ2=0,2) высокая и узкая, а синяя кривая с самой большой дисперсией (σ2=5,0) низкая и широкая. Розовая кривая в отличие от трех других имеет меньшее по величине среднее (μ = –2) и располагается от них левее.
Существует бесконечно большое множество кривых нормального распределения с различными средними (μ) и дисперсиями (σ2). Одно из этих распределений широко применяется в статистическом анализе – это так называемое стандартное нормальное распределение. Оно имеет среднее, равное 0 (μ=0), и дисперсию, равную 1 (σ2=1). На рисунке 4 ему соответствует зеленая кривая.
Таким образом, среднее арифметическое (μ) и дисперсия (σ2) являются основными ПАРАМЕТРАМИ любого нормального распределения, теми величинами, которые полностью его описывают. Статистические методы анализа, использующие для расчетов эти параметры, называются ПАРАМЕТРИЧЕСКИЕ, те, которые не используют, – НЕПАРАМЕТРИЧЕСКИЕ. Прежде чем применять любые параметрические методы анализа, исследователю необходимо доказать, что полученное им эмпирическое распределение количественного признака по своему характеру похоже на нормальное (Гауссово) распределение.
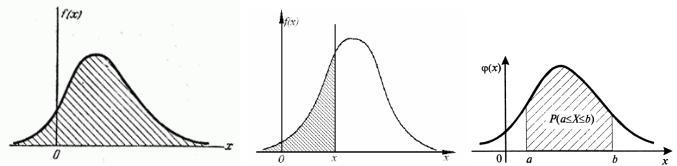
И еще немного теории. Вся площадь под кривой любой функции плотности распределения вероятности есть сумма вероятностей всех возможных значений. Она равна 1,0 или 100% (рисунок 5, А). Любое значение «х» отделяет некоторую часть площади под кривой, которая больше 0,0, но меньше 1,0 (рисунок 5, В). Любые два значения «х», например, «а» и «b», отграничивают некоторую часть площади под кривой, которая также больше 0,0, но меньше 1,0 (рисунок 5, С).
Рисунок 5
Площади под кривой функции плотности распределения вероятности
А) |
В) |
С) |
У любого нормального распределения есть замечательное свойство. Независимо от формы кривой
В интервале μ±1σ площадь под кривой равна 0,683 от всей площади (или 68,3%).
В интервале μ ±2σ площадь под кривой равна 0,955 от всей площади (или 95,5%).
В интервале μ ±3σ площадь под кривой равна 0,997 от всей площади (или 97,7%). Это свойство называется «закон трех сигм» (рисунок 6).
8

Рисунок 6.
«Закон трех сигм» для нормального распределения
Теперь перейдем от теоретического нормального распределения к эмпирическому, полученному в исследовании. Среднее арифметическое (М) и стандартное отклонение (σ) измеряются в одинаковых единицах, и поэтому могут быть отражены на одной числовой прямой. Как мы знаем, площадь под кривой эмпирического распределения соответствует объему исследования. Если эмпирическое распределение похоже на нормальное, то оно должно подчиняться
иего законам.
В интервале М±1σ должно располагаться 68,3% всех единиц наблюдения изучаемой совокупности
В интервале М±2σ должно располагаться 95,5% всех единиц наблюдения изучаемой совокупности
В интервале М±3σ должно располагаться 99,7% всех единиц наблюдения изучаемой совокупности
Проверим, выполняется ли «закон трех сигм» для распределения массы тела студентовпервокурсников. По выборке средняя масса тела равна 60,7 кг, стандартное отклонение 2,0 кг. Используя эти величины можно сформировать следующие интервалы (рисунок 7).
Рисунок 7
Сигмальные интервалы распределения массы тела студентов-первокурсников
54,7 |
56,7 |
58,7 |
60,7 |
62,7 |
64,7 |
66,7 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
М–3σ |
М–2σ |
М–1σ |
М |
М+1σ |
М+2σ |
М+3σ |
||||||
М±1σ или 60,7±2,0 кг (от 58,7 кг до 62,7 кг)
Вэтот интервал попадают значения 59 кг (Р=7), 60 кг (Р=11), 61 кг (Р=9), 62 кг (Р=7). Всего в этом
интервале М±1σ оказалось 34 единицы наблюдения.
(34/55) * 100% = 61,8%
М±2σ или 60,7±4,0 кг (от 56,7 кг до 64,7 кг)
9

В этот интервал попадают значения 57 кг (Р=3), 58 кг (Р=6), 59 кг (Р=7), 60 кг (Р=11), 61 кг (Р=9), 62 кг (Р=7), 63 кг (Р=7), 64 кг (Р=4). Всего в этом интервале М±2σ находятся все, кроме одной, единицы наблюдения, т.е. 54 студента-первокурсника.
(54/55) * 100% = 98,2%
М±3σ или 60,7±6,0 кг (от 54,7 кг до 66,7 кг)
Вэтот интервал попадают все 55 значений нашей выборки от минимального 57 кг до максимального
65 кг.
(55/55) * 100% = 100,0%
При достаточно большом объеме выборочной совокупности можно предполагать, что распределение признака в генеральной совокупности будет похожим на распределение в выборке, т.е. будет иметь примерно такие же параметры М и . То есть в генеральной совокупности значения признака:
близкие к выборочному среднему будут встречаться часто,
отличающиеся от выборочного среднего – будут встречаться реже,
существенно отличающиеся – очень редко.
Следовательно, измерив интересующий нас признак у любой единицы из генеральной
совокупности, можно охарактеризовать полученное значение как нормальное, высокое или низкое. Рисунок 8 показывает, каким образом значения количественного признака традиционно преобразуются в описательный порядковый признак на основе сопоставления с сигмальными интервалами.
Рисунок 8
Оценка количественного признака путем сравнения с сигмальными интервалами
М–3σ |
М–2σ |
М–1σ |
М |
М+1σ |
М+2σ |
М+3σ |
|||||||
Очень |
|
Низкие |
|
Ниже |
|
|
Средние значения |
|
Выше |
|
Высокие |
|
Очень |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|||||||
низкие |
|
|
|
среднего |
|
|
|
|
среднего |
|
высокие |
||
Длительное время в педиатрии оценка физического развития детей осуществлялась по методу сигмальных отклонений, который основан на «законе трех сигм». Данные по конкретному ребенку (рост, масса тела, окружность грудной клетки, окружность головы) сопоставлялись со стандартными показателями для данного пола и возраста. За стандарт принимались средние арифметические значения, полученные на большой выборке здоровых детей. Если показатель физического развития конкретного ребенка находится в пределах М±1σ, то его физическое развитие по этому показателю считалось нормальным (оно и понятно: в соответствии с «законом трех сигм» более 68% здоровых детей данного пола и возраста имеют такие же значения этого признака). Если показатель выходит за границы интервала М±1σ, но остается в пределах М±2σ, то имеются незначительные отклонения от нормы. Если показатель выходит за пределы интервала М±2σ, то физическое развитие ребенка резко отличается от нормы, что говорит о возможном наличии патологии. Это тоже понятно: не более чем у 5% здоровых детей данного пола и возраста значения признака находятся за пределами интервала М±2σ, т.е. для здорового ребенка такая величина признака совершенно не характерна.
Метод сигмальных отклонений использует параметры нормального распределения – среднее арифметическое (М) и стандартное отклонение (σ), т.е. является методом ПАРАМЕТРИЧЕСКОЙ СТАТИСТИКИ. В настоящее время для оценки физического развития детей его не применяют. Используют его НЕПАРАМЕТРИЧЕСКИЙ аналог – центильные таблицы. С центилями мы познакомимся далее в разделе VI, посвященном квантилям.
На «законе трех сигм» основан самый простой метод оценки принадлежности «выскакивающей» варианты к изучаемой совокупности. «Выскакивающая» варианта (выброс, экстремальная варианта) – это очень малое или очень большое значение признака, весьма
10
